前回に引き続き、深層学習について私が勉強していることをメモしていきます。
今回はニューラルネットワークについてです。
相変わらず自分でも書いてて「???」となることがあるので誤ったことが書いてあったら訂正していただけたら幸いです。
ニューラルネットワーク概要
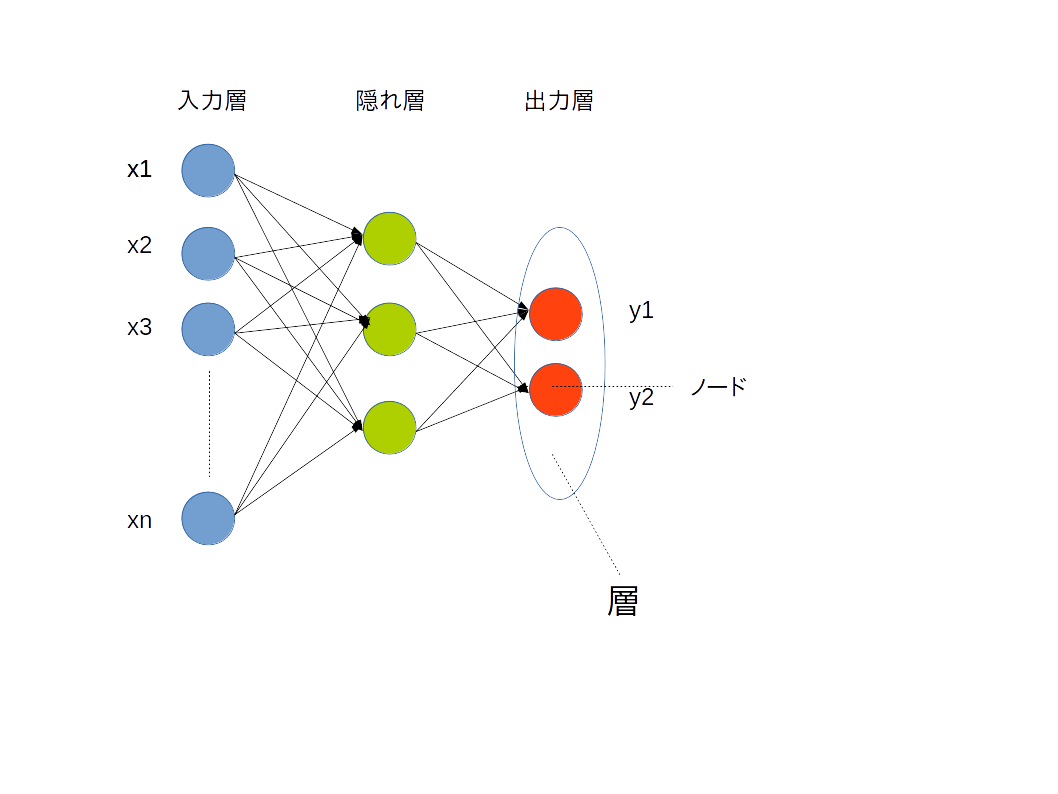
上の図は簡単なニューラルネットワークの構成図です。
-入力層
-隠れ層
-出力層
から構成されます。入力層と出力層は1層だけですが、隠れ層の数は任意です。(この隠れ層の数をパラメータとして最適な数を割り当てることも、精度向上の鍵となる)
各層はノードと呼ばれる任意の数の変数から構成されています。これらのノードが入力層から始まって隠れ層を通過していき、最終的に出力層へ到達します。(活性化関数によって通過しないノードのことも考えると少し適切な言い方ではないかもしれませんが)
まとめると、ニューラルネットワークとは、
m次元のベクトルxをn次元yに移す関数fを推定する方法
と表現することができます。
ノード間のやりとり
では、どのように各ノードは値をやりとりしているのでしょうか?
下の図を見てください。
1対1のノードのやりとりを表しています。
出発するノードはaという値を持っており、aに対して重みwを掛けます。重みwは正負どちらの値もとるため、aは増幅も減衰もします。
そして、到着点であるノードには閾値rが設けられています。
この閾値rをawが超えるのであれば次のノードへawを伝達、超えなければ伝達しないこととします。
なお、この次のノードへ伝達するかしないかの判定をするのは活性化関数という関数の役割です。
誤差逆伝播法
こうしていくつものノードがやりとりを行っていくうちに、m次元だった入力データはn次元のデータへと変換されます。それが出力結果です。
その出力結果は教師データと比較されます。教師データとの誤差が大きい場合は、隠れ層にてかけてきた重みが不適切だったということなので、重みwを更新しなければいけません。
※現時点で筆者は出力データの中身が具体的に何なのか恥ずかしながら理解していません。実際に深層学習フレームワークなどで実装する際にデータを出力させながら確かめていく予定です。
では、どのように重みwを更新すればいいのでしょうか?
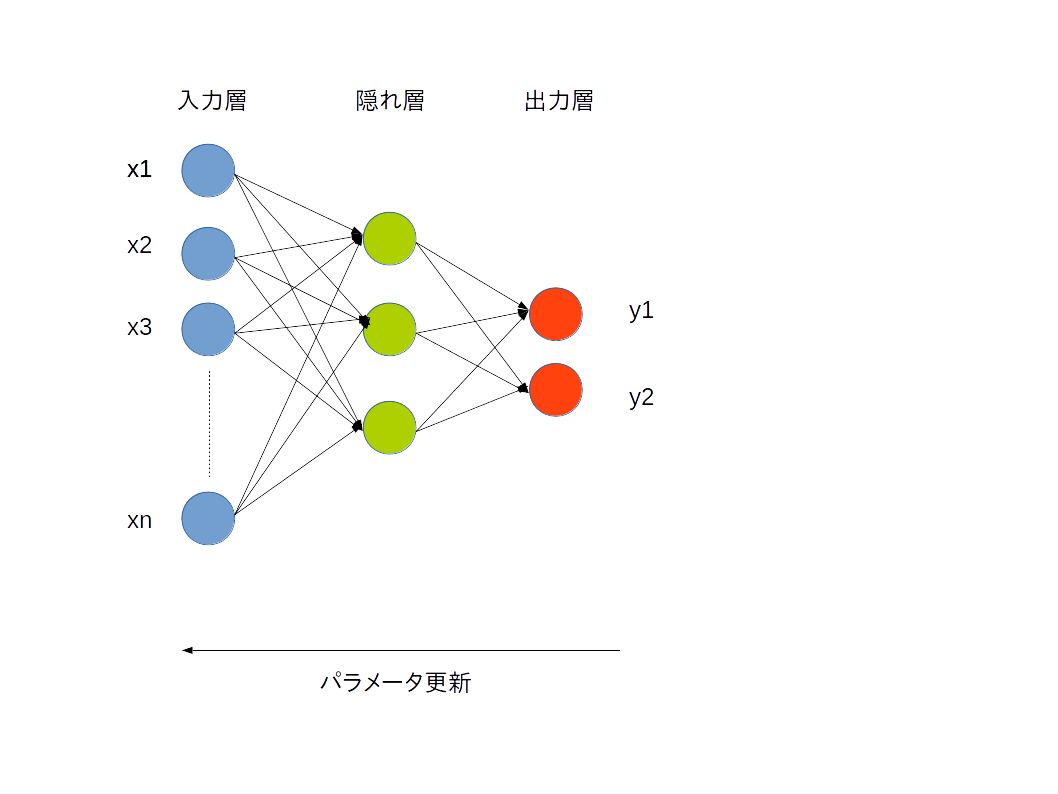
そのための手法が誤差逆伝播法です。
得られた出力結果から、教師データとの誤差を算出して、パラメータとしての重みを調整し、調整された値を元にまた後ろのノードへと更新を伝えていきます。
では、具体的にはどのようにして更新していくのでしょうか?
勾配降下法
重みを調整する方法の一つとして、勾配降下法があります。
これは、誤差が誤差関数を利用して算出されることを利用します。この誤差関数は
-出力と教師データとの差が大きければ大きいほど返り値が大きくなるもの
-微分可能であるものであることが
であることが求められます。
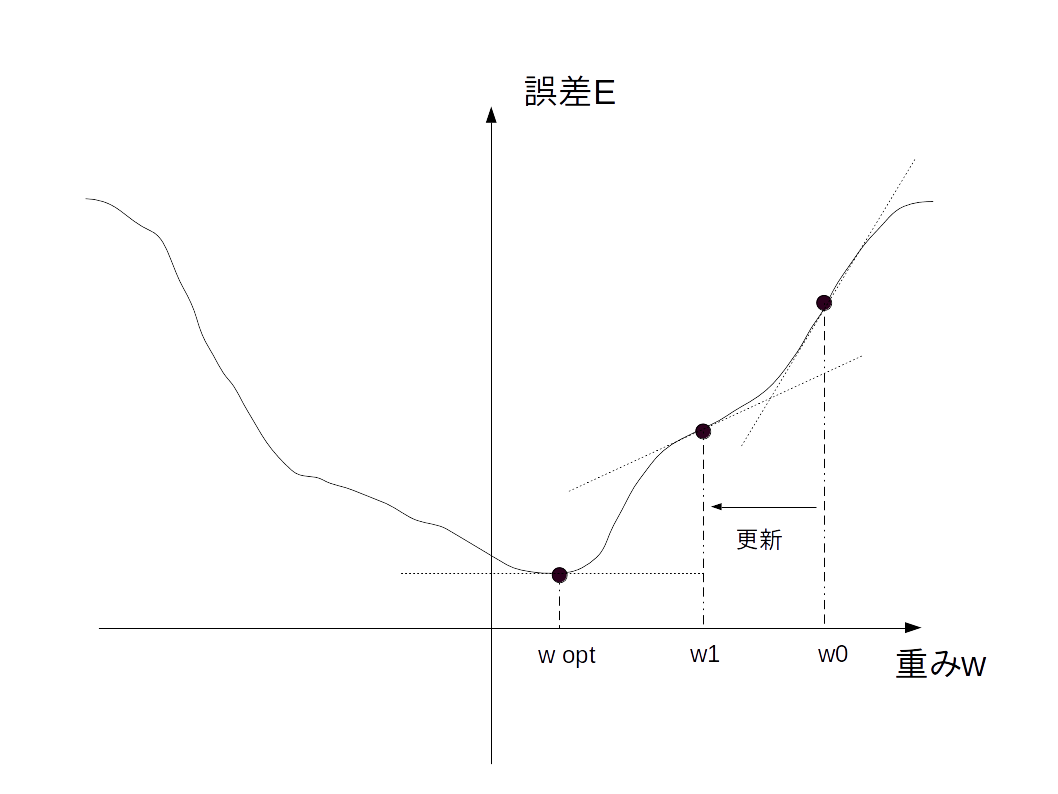
例えば、誤差関数をグラフにすると以下の図になるとします。
誤差は重みwによって決まります。
ここで、微分可能であるということは、最小値を求めることができます。そこが最適なwであるwoptです。
なお、傾き0なのが最小値であることを保証するために下に凸になるよう誤差関数を選ぶ必要があるようです。(このあたりはまだ不安)
更新量Δwは、以下の式で求められます。
Δw = -η\frac{δE}{δw}
誤差が大きいほど傾きは大きくなるため、傾きだけ誤差を更新させます。マイナスをとるのは傾きが正であればwを減少、負であれば増加させるためです。
ηは学習係数で、さすがに傾きをそのまま使ってもうまくwoptを求めることはできないため、誤差を元にどの程度更新するかを決める値です。
この学習係数も精度向上のためにうまく設定する必要があります。
おわりに
今回はここまでにします。
ところどころおかしな点もあると思うので勉強を進めていく中で追記、編集していきます。
参考
山下隆義
イラストでわかるディープラーニング 講談社
新納浩幸
Chainerによる実践深層学習~複雑なNNの実装方法~ オーム社
高卒でもわかる機械学習 (2) 単純パーセプトロン
http://hokuts.com/2015/11/25/ml2_perceptron/
Chainerで始めるニューラルネットワーク
http://qiita.com/icoxfog417/items/96ecaff323434c8d677b