話題の「固有値から固有ベクトルを求める」を検証する

目的

「行列の固有値のみから固有ベクトルを求めることができる」というarxivの論文がTwitterで話題になっていました。

Absolutely Amazing

Physicists (!) discover a new fundamental and amazing mathematical fact:

You can get the Eigenvectors of a matrix using ONLY its Eigenvalueshttps://t.co/JsvjySDdWE pic.twitter.com/Mt797mmqDk

— 〈 Berger | Dillon 〉 (@InertialObservr) November 14, 2019

固有値とか固有ベクトルに敏感な計算化学屋としては「ほんまかいな！」という感想を抱き、論文を参考にこの方法論を実装してみました。

Twitterにて、はかせ Mk-IIさんがRで既に同様の内容を試行されており、二番煎じになってしまいましたが、せっかく書いたので公開します。

話題の「固有値から固有ベクトルを計算する」をRでやってみた。マジ計算できた。
数学の天才、タオ先生も共著の論文はコレhttps://t.co/a4L9Shg8u1 pic.twitter.com/22JcDDzuaP

— はかせ Mk-II (@hshimodaira) November 14, 2019

今回検証する論文

• Peter B. Denton, Stephen J. Parke, Terence Tao, Xining Zhang
• "Eigenvectors from Eigenvalues"
• arXiv:1908.03795 [math.RA]

論文の内容

本記事で使用する文字の定義は以下の通りです。

• $A$: $n \times n$ のエルミート行列
• $\lambda_i(X)$: 行列 $X$ の $i$ 番目の固有値
• $v_{i,j}$: $i$ 番目の固有値に対応する固有ベクトルの $j$ 番目の要素
• $M_j$: $A$ から $j$ 行と $j$ 列を削除した、 $n-1 \times n-1$ の部分行列

当該の公式 (以下、Dentonの式と呼称) は、論文中の式(2)であり、以下の通りです。

|v_{i,j}|^2 \prod_{k = 1; k \neq 1}^n{(\lambda_i(A) - \lambda_k(A))} = \prod_{k = 1}^{n-1}{(\lambda_i(A) - \lambda_k(M_j))}

総乗記号で書かれているファクターで両辺を割ることにより、実装するworking equationが得られます。

|v_{i,j}|^2 = \frac{\prod_{k = 1}^{n-1}{(\lambda_i(A) - \lambda_k(M_j))}}{\prod_{k = 1; k \neq 1}^n{(\lambda_i(A) - \lambda_k(A))}}

注意すべき事項は、3点あります。

1. 行列 $A$ がエルミート行列であること (実数範囲に限れば転置行列であること)
2. 求められるのは固有ベクトル要素の絶対値の2乗
3. 行列 $A$ の固有値に加え、部分行列 $M$ の固有値も必要

[1]は大前提であり、任意の行列に対してDentonの式が成り立つわけではありません。
また、[2]はDentonの式の最大のlimitationです。あくまで各要素のノルムが求まるのみで、符号まで求めることはできないようです。[3]についてはTwitterで誇大広告されていたので、念のため補足です。

実装してみた

Dentonの式をPythonで実装してみました。
なお、ここではあくまで可読性を優先し、高速化については何もケアしていません。
論文の式をなるべくその通りに実装しました。

プログラムの流れは以下の通りです。

1. エルミート行列 (ここでは転置行列) A を生成
2. numpy.linalg.eig 関数で固有値 w・固有ベクトル v・固有ベクトル要素の2乗 v_sq を求める
3. 部分行列 M の固有値 w_M を求める
4. Dentonの式により固有ベクトル要素の2乗 v_sq_denton を求める
5. v_sq_denton を v_sq と比較

以下が今回実装したコードです。Jupyter Notebookにてご実行ください。

# 固有値 (と部分行列の固有値) から固有ベクトルを求める

# [Ref.]
# Peter B. Denton, Stephen J. Parke, Terence Tao, Xining Zhang
# "Eigenvectors from Eigenvalues"
# arXiv:1908.03795 [math.RA]

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.set_printoptions(precision=10, suppress=True)

# 行列 A の次元数
n = 5

# テスト用行列の生成 (エルミート行列; ここでは転置行列とする)
A = np.random.rand(n, n)
for i in range(n):
  for j in range(i):
      A[j, i] = A[i, j]
print('Sample matrix, A\n{}\n'.format(A))

# 固有値 w ・固有ベクトル v を求める
w, v = np.linalg.eig(A)
# 固有ベクトル要素の2乗 (Conventionalな方法による正解値)
v_sq = v * v
print('Eigenvalues, w\n{}\n'.format(w))
print('Eigenvectors, v\n{}\n'.format(v))
print('Eigenvectors^2, v_sq\n{}\n'.format(v_sq))

# 部分行列 M の固有値 w_M を求める
print('Eigenvalues of the submatrices')
w_M = np.empty((n, n-1))
for j in range(n):
  M = np.delete(A, j, 0)
  M = np.delete(M, j, 1)
  w_M[j], v_M = np.linalg.eig(M)
  print('w_M_{}: {}'.format(j, w_M[j]))
print()

# Dentonの式に従って、固有ベクトル要素の2乗 v_sq_denton を求める
# i, jの添字に注意
# (論文) v_{i, j} = (コード) v[j, i]
print('Eigenvectors')
print('v_sq[j, i]: Conventional, Denton\'s    , diff')
v_sq_denton = np.empty((n, n))
for i in range(n):
  for j in range(n):
    lhs_factor = 1
    rhs_factor = 1
    for k in range(n):
      if k == i: continue
      lhs_factor *= w[i] - w[k]
    for k in range(n-1):
      rhs_factor *= w[i] - w_M[j, k]
    v_sq_denton[j, i] = rhs_factor / lhs_factor
    print('v_sq[{}, {}]: {:.10f}, {:.10f}, {:.10f}'.format(j, i, v_sq_denton[j, i], v_sq[j, i], v_sq_denton[j, i] - v_sq[j, i]))
print()

# 要素のグラフ描画
plt.scatter(v_sq, v_sq_denton)
plt.title('Comparison of the elements of v_sq')
plt.xlabel('Conventional')
plt.ylabel('Denton\'s')

実行結果は以下の通りです。

Sample matrix, A
[[0.4275444167 0.2021966017 0.4543530107 0.673879167  0.2269898714]
 [0.2021966017 0.7013023217 0.7657909754 0.5382728785 0.6066537223]
 [0.4543530107 0.7657909754 0.9052402256 0.8992738777 0.6435490638]
 [0.673879167  0.5382728785 0.8992738777 0.0393977905 0.540333617 ]
 [0.2269898714 0.6066537223 0.6435490638 0.540333617  0.412293666 ]]

Eigenvalues, w
[ 2.8335116896 -0.6807938842  0.4370554003 -0.0312361072 -0.0727586781]

Eigenvectors, v
[[-0.3082429717 -0.3636197521  0.7636026622 -0.419137164  -0.1183298706]
 [-0.4627376423 -0.0528009995 -0.5347006838 -0.4303339197 -0.5585640744]
 [-0.5897034002 -0.3030104546  0.0155009696  0.7450240127 -0.0716484798]
 [-0.4301641581  0.8671902412  0.2490698532  0.0097650235  0.0284382686]
 [-0.3975787239 -0.1454595487 -0.2621642255 -0.2897940994  0.8173505837]]

Eigenvectors^2, v_sq
[[0.0950137296 0.1322193241 0.5830890258 0.1756759623 0.0140019583]
 [0.2141261256 0.0027879455 0.2859048212 0.1851872824 0.3119938252]
 [0.3477501002 0.0918153356 0.0002402801 0.5550607795 0.0051335047]
 [0.1850412029 0.7520189145 0.0620357918 0.0000953557 0.0008087351]
 [0.1580688417 0.0211584803 0.0687300812 0.0839806201 0.6680619768]]

Eigenvalues of the submatrices
w_M_0: [ 2.5861888095  0.0895379956 -0.0702008958 -0.5472919056]
w_M_1: [ 2.2587859868 -0.678301828   0.251236573  -0.047244633 ]
w_M_2: [ 1.8128528397 -0.5967806502  0.4368433174 -0.0723773121]
w_M_3: [ 2.2078730813  0.3433691151 -0.0313333691 -0.0735281972]
w_M_4: [ 2.381029619  -0.6653201751  0.3936866351 -0.0359113246]

Eigenvectors
v_sq[j, i]: Conventional, Denton's    , diff
v_sq[0, 0]: 0.0950137296, 0.0950137296, 0.0000000000
v_sq[1, 0]: 0.2141261256, 0.2141261256, 0.0000000000
v_sq[2, 0]: 0.3477501002, 0.3477501002, 0.0000000000
v_sq[3, 0]: 0.1850412029, 0.1850412029, 0.0000000000
v_sq[4, 0]: 0.1580688417, 0.1580688417, 0.0000000000
v_sq[0, 1]: 0.1322193241, 0.1322193241, 0.0000000000
v_sq[1, 1]: 0.0027879455, 0.0027879455, 0.0000000000
v_sq[2, 1]: 0.0918153356, 0.0918153356, 0.0000000000
v_sq[3, 1]: 0.7520189145, 0.7520189145, -0.0000000000
v_sq[4, 1]: 0.0211584803, 0.0211584803, -0.0000000000
v_sq[0, 2]: 0.5830890258, 0.5830890258, -0.0000000000
v_sq[1, 2]: 0.2859048212, 0.2859048212, -0.0000000000
v_sq[2, 2]: 0.0002402801, 0.0002402801, -0.0000000000
v_sq[3, 2]: 0.0620357918, 0.0620357918, -0.0000000000
v_sq[4, 2]: 0.0687300812, 0.0687300812, -0.0000000000
v_sq[0, 3]: 0.1756759623, 0.1756759623, -0.0000000000
v_sq[1, 3]: 0.1851872824, 0.1851872824, -0.0000000000
v_sq[2, 3]: 0.5550607795, 0.5550607795, -0.0000000000
v_sq[3, 3]: 0.0000953557, 0.0000953557, 0.0000000000
v_sq[4, 3]: 0.0839806201, 0.0839806201, -0.0000000000
v_sq[0, 4]: 0.0140019583, 0.0140019583, -0.0000000000
v_sq[1, 4]: 0.3119938252, 0.3119938252, -0.0000000000
v_sq[2, 4]: 0.0051335047, 0.0051335047, 0.0000000000
v_sq[3, 4]: 0.0008087351, 0.0008087351, -0.0000000000
v_sq[4, 4]: 0.6680619768, 0.6680619768, 0.0000000000

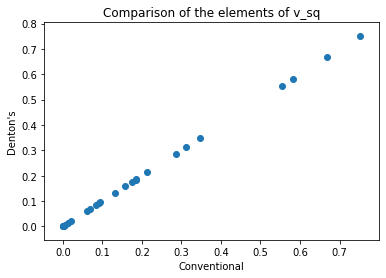
各固有ベクトル要素の2乗値をプロットしてみました。
横軸がconventionalな方法に基づく正解値、縦軸がDentonの式に基づく値となります。
両者がバッチリ一致していることが確認できます。

まとめ

• 本当に「固有値から固有ベクトルを求める」ことができました。
• 正確に表現すれば、「固有値と部分行列の固有値から、固有ベクトル要素のノルムを求める」ことができました。
• しかも、固有値の差を乗算するだけで…すごい！
• なお、この問題において、符号については原理的に求めることができないようです (NP困難)。

これ正確にはエルミート行列の固有値から各固有ベクトル成分の2乗ノルムを厳密に求めるというものですね。各固有ベクトル成分の絶対値からその符号を全て決定する問題はNP困難（前に研究の過程で示した）なので固有値のみから各固有ベクトルを符号込みで厳密に計算するのはやはり無理ぽいです。残念 https://t.co/8ZaD7ekGzo

— みてい (@ubnqf) November 14, 2019