3/19追記:Webアプリ化しました
麻雀YouTuberの麻雀カッコイイシリーズが投稿していた「銀河麻雀」。
(ルール説明は13:40くらいから)
簡単に言えば、各種類の牌に1枚ずつ「ギャラクシー牌(銀河牌)」と呼ばれる牌種が自由になる牌が入った状態での麻雀だ。
例えば、銀河1mは1p,1sとしても扱える。
銀河東は東南西北、銀河白は發中としても扱える。
銀河牌がたくさん入ると、受け入れや待ちの数が通常よりも多くなる。
銀河牌が沢山入った順子が並べば、とても人間の頭では処理しきれない、まさに銀河が広がるような麻雀となる。
というわけで、人間にできない事はコンピュータに任せよう。
この銀河麻雀の待ちを判定するプログラムを作成した。
コード
早速だが、今回書いたコードを載せる。
突貫工事で作ったので、いろいろ汚いのは御愛嬌。
suhai_seq = ["m", "p", "s"]
jihai_seq = ["e", "s", "w", "n", "h", "g", "r"]
jihai_kanji = ["東", "南", "西", "北", "白", "発", "中"]
class tehai:
def __init__(self, manzu, pinzu, souzu, jihai):
# 数牌はマンピンソーの順で0-8、字牌はeswnhgr=東南西北白発中
# 入力は文字列として扱う
self.suhai = [[0 for j in range(9)] for i in range(3)]
self.jihai = [0 for _ in range(7)]
self.suuhai_input([manzu, pinzu, souzu])
self.jihai_input(jihai)
def suuhai_input(self, hai):
for j in range(3):
for i in range(9):
# if hai[j].count(str(i + 1)) > 4:
# print("同じ牌が5枚以上あります。")
self.suhai[j][i] = hai[j].count(str(i + 1))
if sum(self.suhai[j]) != len(hai[j]):
print("1~9以外の入力が含まれます。")
def jihai_input(self, hai):
for i in range(7):
self.jihai[i] = hai.count(jihai_seq[i])
# if hai.count(jihai_seq[i]) > 4:
# print("同じ牌が5枚以上あります。")
if sum(self.jihai) != len(hai):
print("所定の形式以外の入力が含まれます。")
def output_tehai(self):
output_string = ""
for i in range(3):
t = ""
for j in range(9):
t += str(j + 1) * self.suhai[i][j]
if t != "":
output_string += t + suhai_seq[i]
for i in range(7):
output_string += jihai_kanji[i] * self.jihai[i]
return output_string
def add_hai(self, tsumo):
if len(tsumo) == 1:
for i in range(7):
if tsumo == jihai_seq[i]:
self.jihai[i] += 1
break
if len(tsumo) == 2:
for i in range(3):
if tsumo[1] == suhai_seq[i]:
self.suhai[i][int(tsumo[0]) - 1] += 1
break
def discard_hai(self, tsumo):
if len(tsumo) == 1:
for i in range(7):
if tsumo == jihai_seq[i]:
self.jihai[i] -= 1
break
if len(tsumo) == 2:
for i in range(3):
if tsumo[1] == suhai_seq[i]:
self.suhai[i][int(tsumo[0]) - 1] -= 1
break
def ukewatashi(self, haisyu):
ret = ""
if haisyu == "m":
for i in range(9):
ret += str(i + 1) * self.suhai[0][i]
if haisyu == "p":
for i in range(9):
ret += str(i + 1) * self.suhai[1][i]
if haisyu == "s":
for i in range(9):
ret += str(i + 1) * self.suhai[2][i]
if haisyu == "j":
for i in range(7):
ret += jihai_seq[i] * self.jihai[i]
return ret
def maisuu(self):
return (
sum(self.suhai[0])
+ sum(self.suhai[1])
+ sum(self.suhai[2])
+ sum(self.jihai)
)
def agari(self):
if self.maisuu() % 3 != 2:
print("枚数がおかしいです。")
if self.maisuu() == 2:
if 2 in self.suhai[0] + self.suhai[1] + self.suhai[2] + self.jihai:
return True
# 14枚の場合だけチートイロジックを実行
if self.maisuu() == 14:
toitsu_flag = 0
for m in self.suhai[0] + self.suhai[1] + self.suhai[2] + self.jihai:
if m == 2:
toitsu_flag += 1
if toitsu_flag == 7:
return True
flag = False
# 数牌
for i in range(3):
for j in range(9):
# 5枚目があったらFalseを返す。5枚使いOKらしいのでコメントアウトしておく
# if self.suhai[i][j] > 4:
# return False
# 刻子を抜く
if self.suhai[i][j] >= 3:
self.suhai[i][j] -= 3
nT = tehai(
self.ukewatashi("m"),
self.ukewatashi("p"),
self.ukewatashi("s"),
self.ukewatashi("j"),
)
flag = flag or nT.agari()
self.suhai[i][j] += 3
if j >= 7:
continue
# 順子を抜く
if self.suhai[i][j] and self.suhai[i][j + 1] and self.suhai[i][j + 2]:
self.suhai[i][j] -= 1
self.suhai[i][j + 1] -= 1
self.suhai[i][j + 2] -= 1
nT = tehai(
self.ukewatashi("m"),
self.ukewatashi("p"),
self.ukewatashi("s"),
self.ukewatashi("j"),
)
flag = flag or nT.agari()
self.suhai[i][j] += 1
self.suhai[i][j + 1] += 1
self.suhai[i][j + 2] += 1
# 字牌
for i in range(7):
# 刻子を抜く
if self.jihai[i] >= 3:
self.jihai[i] -= 3
nT = tehai(
self.ukewatashi("m"),
self.ukewatashi("p"),
self.ukewatashi("s"),
self.ukewatashi("j"),
)
flag = flag or nT.agari()
self.jihai[i] += 3
return flag
def machi(self):
if self.maisuu() % 3 != 1:
return "枚数が不正です。"
machi_suuhai = ["", "", ""]
machi_jihai = ""
for i in range(3):
for j in range(9):
self.suhai[i][j] += 1
if self.agari():
machi_suuhai[i] += str(j + 1)
self.suhai[i][j] -= 1
for i in range(7):
self.jihai[i] += 1
if self.agari():
machi_jihai += jihai_seq[i]
self.jihai[i] -= 1
nT = tehai(machi_suuhai[0], machi_suuhai[1], machi_suuhai[2], machi_jihai)
return nT.output_tehai()
def machi_flag(self):
if self.maisuu() % 3 != 1:
return "枚数が不正です。"
machi_flag = [False for _ in range(34)]
for i in range(3):
for j in range(9):
self.suhai[i][j] += 1
if self.agari():
machi_flag[i * 9 + j] = True
self.suhai[i][j] -= 1
for i in range(7):
self.jihai[i] += 1
if self.agari():
machi_flag[27 + i] = True
self.jihai[i] -= 1
return machi_flag
def tenpai(self):
if self.machi():
return True
return False
def galaxy_mahjong(T, galaxyhai):
flag = [False for _ in range(34)]
in_galaxyhai = galaxyhai[:]
if in_galaxyhai:
galaxy = in_galaxyhai.pop()
if galaxy.isnumeric():
for i in range(3):
T.add_hai(galaxy + suhai_seq[i])
new_flag = galaxy_mahjong(T, in_galaxyhai)
for j in range(34):
flag[j] = flag[j] or new_flag[j]
T.discard_hai(galaxy + suhai_seq[i])
else:
if galaxy in jihai_seq[:4]:
for i in range(4):
T.add_hai(jihai_seq[i])
new_flag = galaxy_mahjong(T, in_galaxyhai)
for j in range(34):
flag[j] = flag[j] or new_flag[j]
T.discard_hai(jihai_seq[i])
elif galaxy in jihai_seq[4:]:
for i in range(3):
T.add_hai(jihai_seq[i + 4])
new_flag = galaxy_mahjong(T, in_galaxyhai)
for j in range(34):
flag[j] = flag[j] or new_flag[j]
T.discard_hai(jihai_seq[i + 4])
else:
flag = T.machi_flag()
return flag
def main():
print("manzu:")
manzu = input()
print("pinzu:")
pinzu = input()
print("souzu:")
souzu = input()
print("jihai:")
jihai = input()
print("galaxy:")
galaxy = input()
galaxyhai = []
for s in galaxy:
galaxyhai.append(s)
T = tehai(manzu, pinzu, souzu, jihai)
if (T.maisuu() + len(galaxyhai)) % 3 != 1:
print("枚数がちがいます。")
return None
flag = galaxy_mahjong(T, galaxyhai)
output_string = ""
for i in range(3):
t = ""
for j in range(9):
if flag[i * 9 + j]:
t += str(j + 1)
if t:
output_string += t + suhai_seq[i]
for i in range(7):
if flag[27 + i]:
output_string += jihai_kanji[i]
print(output_string + "待ち")
main()
つかいかた
pythonでこちらを実行し、マンズ、ピンズ、ソーズ、字牌、銀河牌を順に入力すると、待ちを出力してくれる。
- 数字の順番は適当でよい。
- 銀河牌は牌種を指定する必要はない。
- 字牌は東南西北白發中=eswnhgrとして入力すること。
- 副露している場合はメンツをそのまま除くこと。枚数が13枚、10枚、7枚、4枚のいずれかになっていれば待ちは出力できる。
- 役があるかどうかの判定はできないので、役無しのアガリになっている場合がある。
- 七対子には対応しているが、国士無双には対応していない。
ということで、以下実際に使ってみたイメージ。
銀河には人類が発見していない当たり牌"ダークマター"が存在します。ダークマターを見逃し誤ロンやフリテンをしてしまうことが多々あります。このロンを"ダークマターストライク"と名付けます。
— 肥えD-Koedammit-@たりんちゅ (@tikinnyaro) March 17, 2022
さて、2mでロンしまったこの人の待ちは?#銀河麻雀#麻雀星人 pic.twitter.com/YnljdkOXGA
こちらを試してみよう。
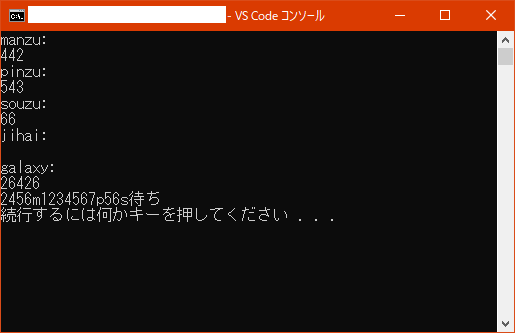
こんな感じで、この手牌は2456m1234567p56s待ちだということが分かる。
打5sで47全部と1sp
— お知らせ/天鳳 お紙らせ/雀魂 (@shirase_ccr) March 16, 2022
77m 67p8g 234p 56g 2g3s4g
打7mで25全部と8mp
67p8g 56g7m 234p 2g 3s4g5s https://t.co/CTVUmUEG1S
こちらの7m切りの場合も…

258m258p25s待ちと分かる。
注意点
突貫で作ったので、だいぶ遅い。
銀河牌の種類にもよるが、銀河牌が5枚で15秒くらい、6枚だと50秒くらいかかる場合がある。
7枚以上はあまり実用に耐えない速度となるので注意。
全パターンを解析しているだけなので、銀河牌が1枚増えるごとに3倍時間がかかる。
- 牌種が1パターンしかないことが明らかな場合は、銀河でない牌として入力すると多少早くなる。
(銀河9が9mにしかならない時はマンズに入力する、など) - あまり無いケースだが、確定メンツがあればそれを入力しないことでだいぶ早くなる。
(銀河牌が5~9しかないときの123や、字牌暗刻など。雀頭は取り除けないので注意)
今後やりたいこと
↑簡単にできそうなこと
- 高速化する
- オンライン実行環境でも実行できるように調整
- 「何切って何待ち」の実装
- webアプリとして公開する(誰かやって♡)
- 牌をどれに取ることによってどの待ちが生まれるのかを表示する
- 純正祝儀の枚数を計算
↓難しそう・面倒そうなこと
おまけ:ロジックの概要
(ここから先はプログラミング興味ない人は読まなくていいよ)
銀河麻雀の待ちを判定するにあたっては、いくつかのプロセスを踏む必要がある。
最も簡単で、最初に実装すべきなのは「アガリ形になっているかどうか」を判定するプログラムである。
麻雀のアガリ形が4面子1雀頭であることから考えると、この問題は「メンツを4回抜いて、同じ牌2枚のみが残る状態にできるか」という問題に置き換えられそうである。
メンツを抜く操作は、同じ牌を3枚抜くか、並んだ数牌を3枚抜くかなので、そこまで難しくはない。
注意点として、副露している場合は手牌のメンツの数が減る。そのため、メンツを抜く回数は可変にしておきたい。
これを実装するには、再帰関数を利用するのがよさそうだ。
ということで、今回はagari()メソッド内でこの操作を実装している。
メンツを抜いた状態を渡して再帰させることで、副露しているかどうかに関わらず1つのコードで実装ができる。
ちなみに、メンチンの待ちを判定するプログラムがいちばん簡単に書けるので、プログラミングの練習として皆さんもやってみて欲しい。
今回は3種の牌と字牌まで実装しなければならないので結構面倒だった。
「アガリかどうか判別する」プログラムさえできてしまえば、待ちを探すプログラムはとても簡単。
13枚の手牌に34種類の牌を1つずつ足して、アガリになっているか判別するだけである。
今回はmachi()メソッドおよびmachi_flag()メソッドによってこれを実装している。
ただし、この方法ではどういう形の待ちなのか(両面、シャンポン、など)までは判別できないので、それを実装したいなら別途方法を考える必要がある。
待ち判別のプログラムまでできれば、いよいよ銀河麻雀の待ち判別だ。
銀河牌について、マンピンソーのすべてのパターンを調べ上げればいい、という事はすぐに思いつく。
だが問題点として、銀河牌の枚数が毎回異なるため、全てのパターンを列挙するところが少し難しい。
結論から言えば、こちらも再帰関数の実装により、枚数の異なる銀河牌に対応できる。
galaxy_mahjong()メソッドで実装しているので、参考にして欲しい。
最後に、計算量について。
アガリ形判別の計算量$N1$ → 刻子34種類、順子21種類を抜けるかどうかの判定を最大4回実施するため、大きめに見積もって$(34+21)^4≒10^7$
待ち判別の計算量$N2$ → 34種の牌で計算するので $N1×34$
銀河麻雀の計算量$N3$ → 数牌の場合、銀河牌1枚につき3パターンあるので$N2×3^g$(gは銀河牌の枚数)
ということで、ある程度枝刈りをしなければかな~り大きな計算量になることがわかる。
今回は全然枝刈りをせずにほぼそのまま実装したので、結構遅くなってしまった。
近いうちにもう少し高速化をしたいと思う。
3/19追記:Webアプリ化しました