こんにちは。
9/9にPCK2023予選に参加したのでその参加記と問題の解法をまとめます。自己満です。
ところで問題言及ってしていいんでしょうか?いいですよね?
結果
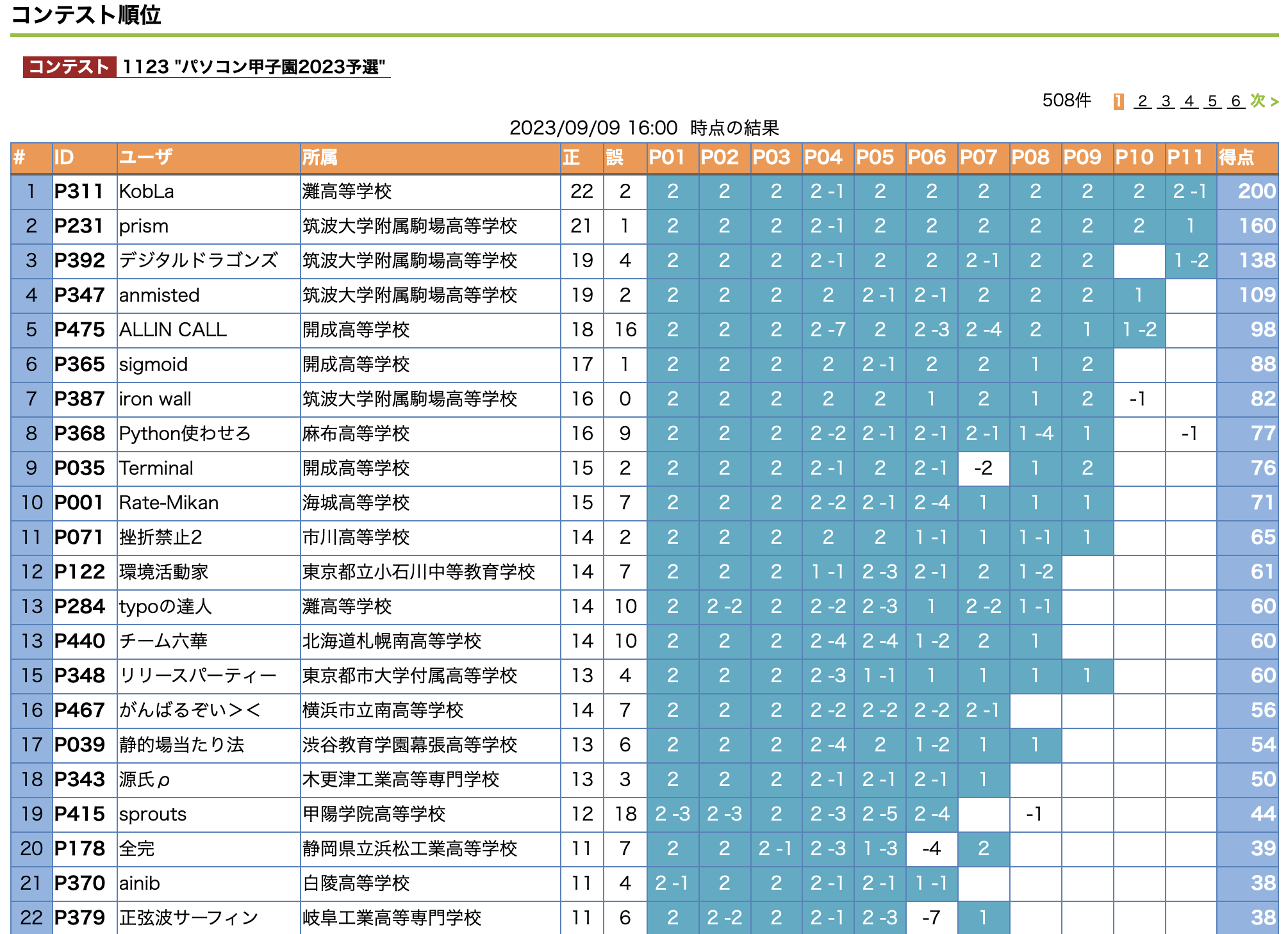
とりあえず結果です。
チーム「typoの達人」で参加して、16時時点で13位でした。
AtCoder 水・緑 のチームで出たので割といい成績を取れたんじゃないかと思ってます。(16時以降で変動してるかもしれないけど)
流石に本選いけてると信じたい。
あと、ちゃっかり問題4のFAを取ってました
予選当日
何故か朝からテンションがクソ高かったです。ハイでした。
そのおかげで結構リラックスできてたと思います。
13:30から競技開始なので13:10くらいに学校に着けばいいかなと思い、家を出るまではAtCoderの青diffを何問か解いて精進してました。
朝食はコーンフレーク
問題解説
8完だったのでそこまでは書きます。
記事を書いている時点ではまだ過去問は公開されてないので言及していいのか分からん。
問題1
$A \quad mod \quad (N + 1)$だけです。
書くことない。
提出した瞬間、NA という見慣れない文字が見えてしまって一瞬不正解かと思ってしまいました。
ジャッジ中なだけでした。
問題2
原点からのマンハッタン距離が$d$以下かどうか判定すればいいだけです。
私はマンハッタン距離ではなくユークリッド距離で判定してて1ペナしました。問題はよく読みましょう。
問題3
セグ木の実装とかやったことある人はこの問題がそのまま実装に当てはまりそう。
$2$で割り続ける。
問題4
正解率も低かったみたいです。この問題をペナを出さずにFAできたのは嬉しいね。
まずは辺の長さが同じかどうか判定します。
あとは直角かどうかの判定ですが、直交座標系だし僕は内積を使いました。
問題5
素因数分解するだけ。
問題6
入力形式が見慣れないタイプでしたが、
$dist_{i,j,k} := マス (i, j) にk拍目で到達するための最短距離$
とすればBFSで解けます。添字管理が少し大変でした。
問題7
ソートしたあとのindexと、元々のindexが分かれば、ボールはそのindexの間しか動きません。
したがってその範囲の箱の大きさの区間最小値が分かれば解けます。
何を使ってもいいですが、僕はセグメント木を生やしました。
問題8
まず、$N \leq 8$ なので順列全探索だろうと予想が立ちます。
あとはゴリゴリに数学をします。
なお、ベクトルのライブラリがあると楽らしいのですが、僕は持っていないので数学をしました。
現在のユアサ君の位置を$A=(X,Y)$とします。今取りに行こうとしているボールの現在の位置を$B=(x_i,y_i)$として、ユアサ君とボールの座標が一致する点を$C$とし、$\angle ACB = \theta$ 、$\overrightarrow{AC}$ の偏角($x$軸から測った角度)を$\alpha$、$\overrightarrow{BC}$の偏角を$\beta$とおくことにします。
$d=|\overrightarrow{AB}|$
とすると、余弦定理より、ユアサ君とボールが$C$に到達するまでの時間を$T$として
$d^2=T^2v^2 + T^2(s^2_i + t^2_i) - 2 T^2 v \sqrt{s^2_i + t^2_i} \cos{\theta}$
が成立します。
また、$T$秒後にはユアサ君とボールの位置は$C$になるので、ユアサ君の速度を$\overrightarrow{v} = (v_x, v_y), \quad |\overrightarrow{v}| = v$ として、
$(X,Y) + T \overrightarrow{v} = (x_i,y_i) + T(s_i, t_i)$
も成立します。
ここで
$v_x = v \cos{\alpha}, \quad v_y = v \sin{\alpha}, \quad \cos{\beta} = \frac{s_i}{\sqrt{s^2_i + t^2_i}}, \quad \sin{\beta} = \frac{t_i}{\sqrt{s^2_i + t^2_i}}$
であるので、以上の式から加法定理などを使って$T$のみの式を作ると、
$(v^2-s_i^2-t_i^2)T^2 + 2(s_i(X - x_i) + t_i(Y - y_i))T - d^2 = 0$
という二次方程式が出てくるので、これの正の解が$T$の値です。
そのあと、ボールの位置を
$(x_i + Ts_i, y_i + Tt_i)$
に更新するとシミュレーションできます。
あとはボールを拾う順番を全探索することで、$O(N^2N!)$で解けます。
感想
問題がちゃんと読めていなかった。母国語さえまともに読めないみたいです。
問題7でindexの管理を間違えて3ペナ出してしまったのがかなり悔やまれる一方、問題8をしっかり通せたのは偉かったと思います。
本選に行けるのであれば他の本選erと会えるのでとても楽しみです!(通っててくれ)