OpenCL SOPでグラフ力学シミュレーション

はじめに

この記事ではHoudiniでネットワーク構造の配置を最適化する方法を紹介します。
Houdini18、USD、PDG、Solaris、Karma！等の新鮮なネタではないですが、、
Houdini16.5で追加されたOpenCL SOPを使用した作例です。

環境

CentOS 7.5.1804
Geforce RTX 2080Ti
Houdini FX 18.0.287 (16.5以上必須)

HIP

HIPファイルはこちら

グラフ力学シミュレーション

英語ではForce Directed Graphなどと書かれているのを見ます。
ぐちゃぐちゃ、ランダムに配置されたネットワークグラフに対し、クーロンの法則とフックの法則の適用を繰り返し、配置を最適化していくといったものです。
ここでいうネットワークグラフとは各ノードがエッジで繋がっている構造です。Houdiniで扱いやすい構造ですね！
詳しくは力学モデル (グラフ描画アルゴリズム) - Wikipediaを参照して下さい。

Wikipediaにあるサンプルコードを見ても分かるとおり、仕組み自体は非常にシンプルです。
Pythonでも出来ますし、頑張ればMaya等でもきっと出来るでしょう。
HoudiniでもVellumを使って簡単にシミュレートすることが出来ます。
2Dならブラウザで動かせるd3-forceなるライブラリーもあります。

が、これらで行う手法は処理が非常に遅いです！
d3やVellumはまだまだ早い方ですが、グラフ力学シミュレーションはその性質上、膨大なループ処理が必要になります。
全てのノードが周囲のノードを参照し位置を調整していく という処理を数十〜数万ループ行います。
もちろん、ノード数・エッジ数が少ないうちならこれらの手法でも問題ありませんが、数千、数万、数十万と増えていくと、
まともな結果が見れるまでにとても長い時間がかかります。。

そこで、これらの処理を並列化し、OpenCL SOPを使用することでGPUの力を使えるようにします。
並列化することで1ループ前のノード位置を参照することになるので、結果は変わってしまいます。
CPUによる全ノードループ処理と比べると、少し劣っているように見えますが、その分爆速なのでトレードオフということにしておきます！

OpenCL SOP

デキる奴です。（NVLink対応してくれたら完璧なんだけど。。）
並列・反復処理が爆速です。
最近使用するまでOpenCLの知識はありませんでしたが、OpenCLの面倒な部分はこのノードが面倒見てくれるので思ったより簡単に扱えます！
たぶん、それなりにWrangleが使える人ならチュートリアル見れば使えるようになると思います。

OpenCL SOPの使い方をここで一から書くと、それだけで記事が1本出来てしまうので簡単にしか書きませんが
OpenCL | Jeff Lait | Houdini 16.5 Masterclassとヘルプを見れば分かると思います！

作例1

データの準備

今回はStanford Large Network Dataset Collectionのデータを使わせてもらいます。
web-NotreDame.txt.gzをダウンロードします。
HIPと同じ階層にtxtファイルを解凍し、テキストエディターで最初の4行を削除し保存します。

データのジオメトリー化

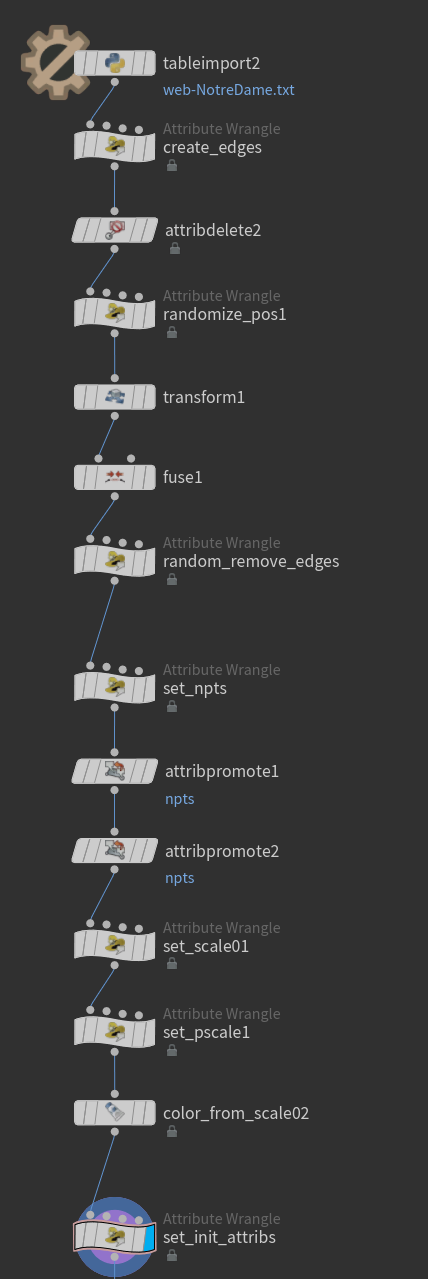
txtファイルをTable Import SOPで読み、0列目をsource/1列目をtargetアトリビュートに格納しました。
全体では150万行弱ありますが、多すぎて調整が大変になるのでひとまずMax Rowsを5000とします。

sourceとtargetポイントを作成し、接続し、idアトリビュートを追加しておきます。
idアトリビュートを元にポジションをランダマイズし、同一ノードが同一位置に来た所でfuseします。念の為 Match Attributeにidを指定しておきます。
複数のクラスターが出来るように、ランダムにエッジを削除します。

ノード毎のエッジ数を正規化しpscaleをセットします。
ついにでpscaleからカラーランプも設定しておきましょう。
次の章で述べますが、OpenCL SOPに渡すための準備も最後にしておきます。

OpenCL SOPにデータを渡す

データの下準備は出来ましたが、OpenCL SOPに渡すための準備はまだ出来ていません。
OpenCL SOPではポイントを生成したり、削除したり、エッジの本数を数えたりなど、ジオメトリー情報に直接アクセス出来ません。
そのため、必要な情報は予めwrangle等でpointアトリビュートにしておき、OpenCL SOPのBindingでパラメーター化してあげる必要があります。
今回は、以下の4つのアトリビュートを新規に作成しました。

i[]@neipts = neighbours(0, @ptnum);
v@v = {0, 0, 0};
v@__v = {0, 0, 0};
v@__P = @P;

neipts(=直接接続されているノード番号のリスト)はバネモデルの計算に必要
vは反復計算で使うVelocity
__vと__Pは計算結果をWrite Back Kernelに渡すアトリビュート。

Write Back Kernelとは...Houdiniヘルプより

カーネルを実行した後に、それにバインドされた同じパラメータのセットで2番目のカーネルを即座に実行することができます。
複数のスレッドが同じデータに書き込みたい時に、それを2回のパス処理に分けることで、競合状態を回避することができます。

これでOpenCL SOPに渡すためのジオメトリー準備は完了です。

OpenCL SOPを使う

Attribute Wrangle SOPのように、Inputにつないで即コード書いてOK！とは行きません。。
まずBindingsを定義し、Generate Kernelで生成されたコードをコピペしてKernelの中身を書いていく流れになります。

Bindings

アトリビュートを渡す場合、以下のように設定します。Writableにチェックを入れないと処理がアトリビュートに反映されません。

定数は以下のように設定しています。

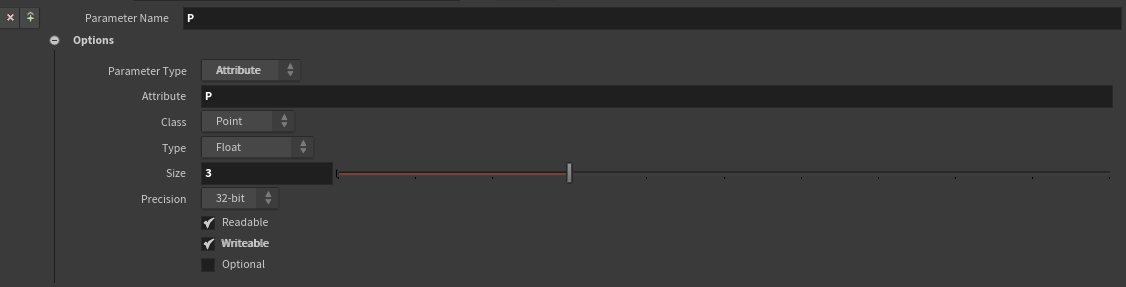
今回設定したパラメーターは以下になります。

アトリビュート名
v@P
v@__P
v@v
v@__v
i[]@nepts

定数名	値	説明
NODE_STRENGTH	0.05	斥力
SPRING_LENGTH	1.05	ばねの長さ
SPRING_STIFFNESS	0.04	ばねの剛性
V_DAMPING	0.015	Velocityの減衰率
STEP	1.0	Force適用倍率

複雑なモデルになってくると、周りからのForceが多すぎて、Velocityがとんでもないことになり結果がぶっ飛んでしまうことがよくあります。
そういった場合はSTEPを小さくして1ループあたりの移動距離を短くします。（その分必要Iteration回数は増えます。）

OpenCL Code

段階的に説明する予定でしたが時間切れとなりました・・！
が、特別難しいことはしていません。

少しだけ解説を書きます。

arrayパラメーターの読み書きにvstore/vloadが紹介されていますが、
OPENCL_DEVICEがCPUの時に動作しないようなので、インデックスでアクセスするようにしています。
GPUで演算したときのパフォーマンスが悪くなるのかと思いきや、ほぼ変わらないようです。

クーロン力・ばねモデルについては、色々な距離減衰・補完方法を試しましたが、テストしていた当時のデータでは
力学モデルを用いた階層型グラフデータ画面配置手法の改良手法とウェブサイト視覚化への応用, p253を参考にしたモデルが一番安定していていい結果が出やすかったので、今回もそちらを採用しています。

Code

#include "interpolate.h" 
float lerpConstant( constant float * in, int size, float pos);

kernel void forceDirectSimulation( 
                 int P_length, 
                 global float * P ,
                 int __P_length, 
                 global float * __P ,
                 int v_attrib_length, 
                 global float * v_attrib ,
                 int __v_length, 
                 global float * __v ,
                 int neipts_length, 
                 global int * neipts_index, 
                 global int * neipts ,
                 float  NODE_STRENGTH ,
                 float  SPRING_LENGTH ,
                 float  SPRING_STIFFNESS ,
                 float  STEP ,
                 float  V_DAMPING 
)
{
    int idx = get_global_id(0);

    if (idx >= P_length){
        return;
    }

    float3 self_pos = {
        P[idx * 3], 
        P[idx * 3 + 1], 
        P[idx * 3 + 2]
    };
    float3 self_v = {
        v_attrib[idx * 3],
        v_attrib[idx * 3 + 1],
        v_attrib[idx * 3 + 2]
    };

    float3 self_force = {0, 0, 0};

    float v_mult = (float)1.0 - V_DAMPING;

    // Coulomb
    for (int i = 0; i < P_length; i++){
        if (i == idx)
            continue;
        float3 pos = {
            P[i * 3],
            P[i * 3 + 1],
            P[i * 3 + 2]
        };

        float3 dist3 = self_pos - pos;
        float dist = length(dist3);

        if (0 < dist && dist < 1){
            float force = NODE_STRENGTH * ((float)1.25 * pow(dist, 3) - (float)2.375 * pow(dist, 2) + (float)1.125);
            self_force += dist3 * force;
        }
    }

    // Spring
    float3 pre_pos = {0, 0, 0};
    int start = neipts_index[idx];
    int end = neipts_index[idx + 1];
    for (int i = start; i < end; i++){
        int neipt = neipts[i];
        float3 pos = {
            P[neipt * 3],
            P[neipt * 3 + 1],
            P[neipt * 3 + 2]
        };

        float3 dist3 = self_pos - pos;
        float edge_length = (min(length(dist3), SPRING_LENGTH) - (float)1);
        float force = -SPRING_STIFFNESS * edge_length;
        self_force += force * dist3;
    }

    self_v = (self_v + self_force) * v_mult;
    self_pos += self_v * STEP;

    __P[idx * 3] = self_pos.x;
    __P[idx * 3 + 1] = self_pos.y;
    __P[idx * 3 + 2] = self_pos.z;

    __v[idx * 3] = self_v.x;
    __v[idx * 3 + 1] = self_v.y;
    __v[idx * 3 + 2] = self_v.z;
}


kernel void writeBack( 
                 int P_length, 
                 global float * P ,
                 int __P_length, 
                 global float * __P ,
                 int v_attrib_length, 
                 global float * v_attrib ,
                 int __v_length, 
                 global float * __v ,
                 int neipts_length, 
                 global int * neipts_index, 
                 global int * neipts ,
                 float  NODE_STRENGTH ,
                 float  SPRING_LENGTH ,
                 float  SPRING_STIFFNESS ,
                 float  STEP ,
                 float  V_DAMPING 
)
{
    int idx = get_global_id(0);
    if (idx >= P_length)
        return;

    P[idx * 3] = __P[idx * 3];
    P[idx * 3 + 1] = __P[idx * 3 + 1];
    P[idx * 3 + 2] = __P[idx * 3 + 2];

    v_attrib[idx * 3] = __v[idx * 3];
    v_attrib[idx * 3 + 1] = __v[idx * 3 + 1];
    v_attrib[idx * 3 + 2] = __v[idx * 3 + 2];
}

実行

Options>Iterationの数値を計算がしっかり収束する辺りまで引き上げます。
サンプルでは1000にしていますが、マシン環境が厳しければ300くらいでも大丈夫です。

計算の過程は一切必要ないのですが、せっかくなのでGIFにしてみました。

今回くらい少ないデータ量(約2400ノード3800エッジ)であれば一瞬ですね。
数万ノード数十万エッジで10000Iteration(ノード／エッジ数が増えるほど必要iterationも増える傾向にあり)となると、
シミュレーションだと最悪数日コースですが、OpenCL SOPを使えば数分で終わります！

作例2

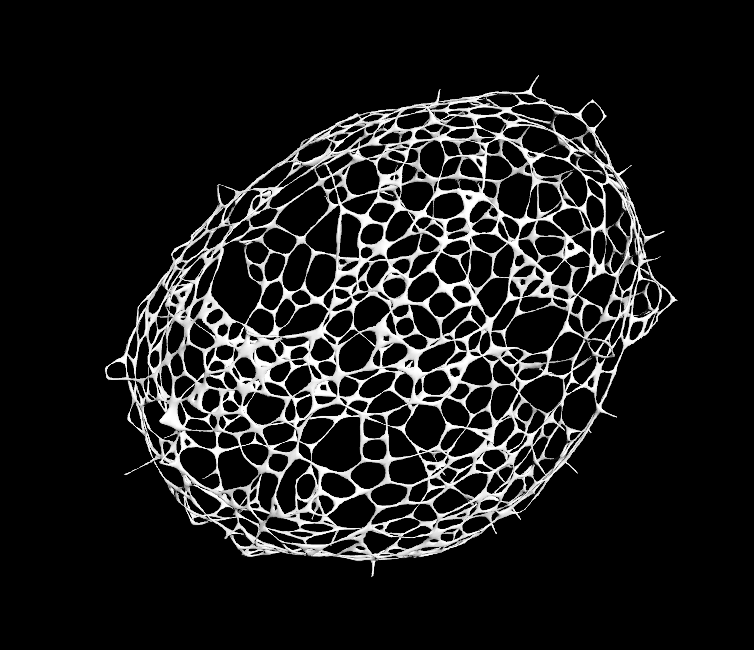
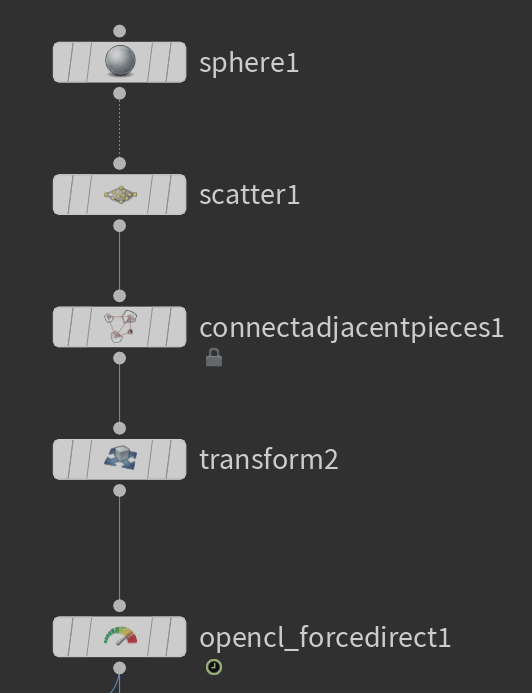
sphereの表面にscatterし、connectadjacentpiecesで接続したジオメトリーを入力してみると、ちょっと違った面白い結果になりました。

Max Search Points=4

Max Search Points=3

まとめ

OpenCL SOPを使った一例の紹介でした。

今回はパラメーターをシンプルにしていますが、
グラフ力学シミュレーションは入力のノード数やエッジ数・初期配置によって大きく結果も最適パラメーターも変わってくるので、
仕事で使おうと思うと色々カスタムしなければ思い通りの結果は出ないかもしれません。
実際私が仕事で作ったHDAでは他に、重力・質量アトリビュート・斥力アトリビュート・特定ノード固定等を実装していたりします。

紹介したOpenCL SOPの用途としてはネットワーク構造のジオメトリーに対する処理でしたが、
Masterclassでも実演しているように、ポリゴンのSmooth処理等もOpenCLで爆速に出来たりします。
反復が多い処理で速度にお困りの方は、置き換えにチャレンジしてみてはいかがでしょうか！

参考

力学モデル (グラフ描画アルゴリズム) - Wikipedia
力学モデルを用いた階層型グラフデータ画面配置手法の改良手法とウェブサイト視覚化への応用
d3-force

OpenCL | Jeff Lait | Houdini 16.5 Masterclass
OpenCL geometry node