TVM 計算機能を使う
GRAPH MATH+ は Ver.2.00 のアップデートで金融計算機能が加わった。
機能自体は fx-CG50 や fx-9750GIII のものと変わらない。
ただしファンクションキーが無いため操作体系が若干異なり、また基本計算モードで変数の値を読み込めない。
GRAPH MATH+ のローン計算は金銭の時間的価値(英語では TVM = Time value of money)の計算式にしたがって変数に値を入れて求めるやり方である。
GRAPH MATH+ のメニューでは Compound Interest (複利計算)がそれにあたる。
日本の金融電卓と違って自由度がある分、慣れるまでに時間がかかる方式である。
具体的なやり方は hp の金融電卓のマニュアルに詳しいのでそちらを参考にされたい(日本語版があるものとしては、 HP12c や HP17bII+ が参考になる)。
金融電卓の TVM 計算は基本的には1種類の定期返済にしか対応していないが、ボーナス併用払い計算の場合は別々に TVM 計算をさせて合算すればよい。そのやり方を例題で検証する。
ボーナス併用払い計算の実際
例題は以下のサイトの計算例を使用した。
3000万円借入、うちボーナス払い分600万円、利率1.35%、30年払いの月額返済額は?
月々返済部分の計算
まずは月々返済額の計算である。
Financial メニューから Compound Interest を選択

Settings の Payment Point を End(期末)に設定
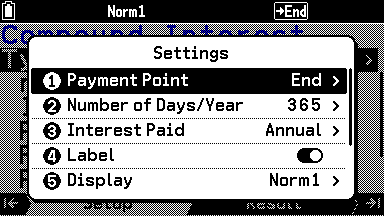
Type を PMT(Payment、定期支払額)にし、各項目を入力。
計算式での入力も可能であるため、 n(支払回数) は 30×12 、 PV(元金) は 30000000-6000000 と入力してよい。
I%(利率)は 1.35 、FV(最終支払い後の残高)は 0 。
P/Y(年間の支払回数) と C/Y(年間の複利回数) はそれぞれ 12 にする。
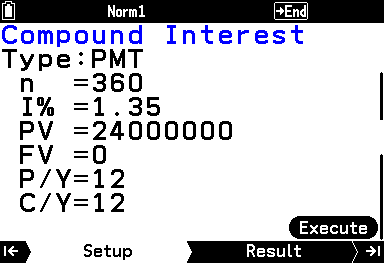
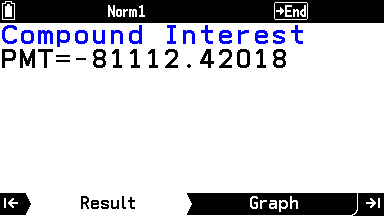
Execute で OK を押すか、右タブキーを押すと月々の支払い額が表示される。
8万1112円。
なお、マイナスの値は支払いを意味する。
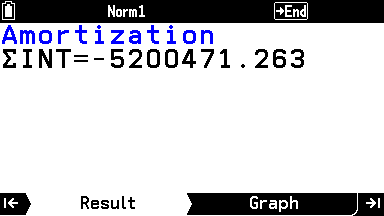
利息の総額を求めるには、 Amortization 機能を使う。

Type を ΣINT(Total Interest)、 PM1 を 1 、 PM2 を 360 に設定する(1回目から360回目の利息総額)。
その他の項目は Compound Interest の値がそのまま反映される。
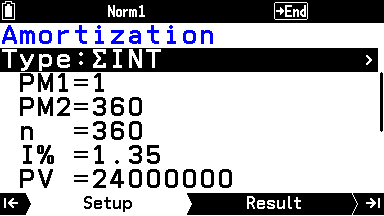
利息総額は520万0471円と求まる。
ボーナス払い部分の計算
続いてボーナス払い。
再び Compound Interest に戻って入力していく。
今度は n = 30×2 、 P/Y = C/Y = 2 となる。
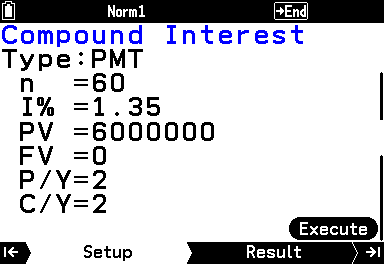
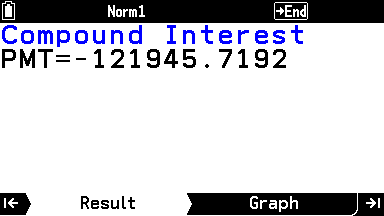
ボーナス払いは毎回12万1945円となる。
Amortization でボーナス払いの利息総額を計算すると、131万6743円。
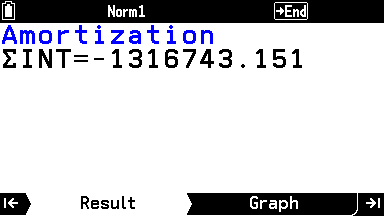
月々払い部分の利息520万0471円と合算すると651万7214円となり、例題の答えと一致することがわかる(結果を変数に代入することができないため、メモしておく必要がある)。
金融電卓としても使えるグラフ電卓
実は CASIO に限らず、 TI や hp のグラフ電卓にも金融計算機能は備わっている(CASIO は金融電卓の機能の大半を網羅しているが、その他のグラフ電卓は TVM 計算が主で、全ての機能を備えているわけではない)。
実際の金融取引に用いる際は金融機関が計算した値と比較するよう説明書に注意がなされているが(以下は fx-CG50 バージョン3.70 ソフトウェア取扱説明書 p7-1 より)、精度は金融電卓と同等と考えてよい。

グラフ電卓の金融計算機能を活用してみてはいかがだろうか。