CASIO Graph Math+ で 情報I の Python 課題をやってみる

「情報Ⅰ」でも Python 優勢？

2022年度に導入された高校の必修科目「情報Ⅰ」。内容にはプログラミングも含まれている。
学習指導要領上は特にプログラミング言語の指定はないものの、教科開始前の教員アンケートでは6割以上の教員が Python を指導予定と答えている。

実際、文部科学省が公開している高等学校情報科「情報Ⅰ」教員研修用教材も本編は Python を使用している（他のプログラミング言語は、JavaScript版・VBA版・ドリトル版・Swift版が章ごと差し替えとして用意されている）。

そこで、教員研修用教材に載っている Python のスクリプトが Graph Math+ の MicroPython でどこまで動くのか試すことにした。

動作結果

• 対象は『高等学校情報科「情報Ⅰ」教員研修用教材』第3章にある Python スクリプト（このPDFに記載のもの）。
• Graph Math+ 単体で動くかどうかを検証。外部制御に関するスクリプトは実行不可とする。
• Graph Math+ は漢字・かなを使用できないため、スクリプト中の日本語は適宜英語やローマ字に置き換えるものとする。これに関してはスクリプトの修正に入れない。
• これらの条件を踏まえ、掲載のスクリプトのまま同じ結果で動作したもの：○、スクリプトを一部修正して動作したもの：△、掲載結果と異なるもの：▲、実行不可：×と判定して表にまとめる。

ページ・図表	判定	備考
p101 図表7	△▲	sysモジュールがない、数値は同じものが使える、Infになる桁数が異なる
p102 図表8	△	0.28-0.27 の結果が 0.01000000000000001 になる
p108 図表6	×	外部制御につき実行不可
p109 図表7	×	外部制御につき実行不可
p110 図表8	×	外部制御につき実行不可
p116 図表7	○
p116 図表10	○
p117 図表13	○
p118 図表16	○
p122 図表2	○
p122 図表3	○
p123 図表4	○
p123 図表5	○
p124 図表9	○
p125 図表11	×	ネットワーク接続が必要なため実行不可
p128 図表3	○
p129 図表6	○
p130 図表9	○
p131 図表11	○
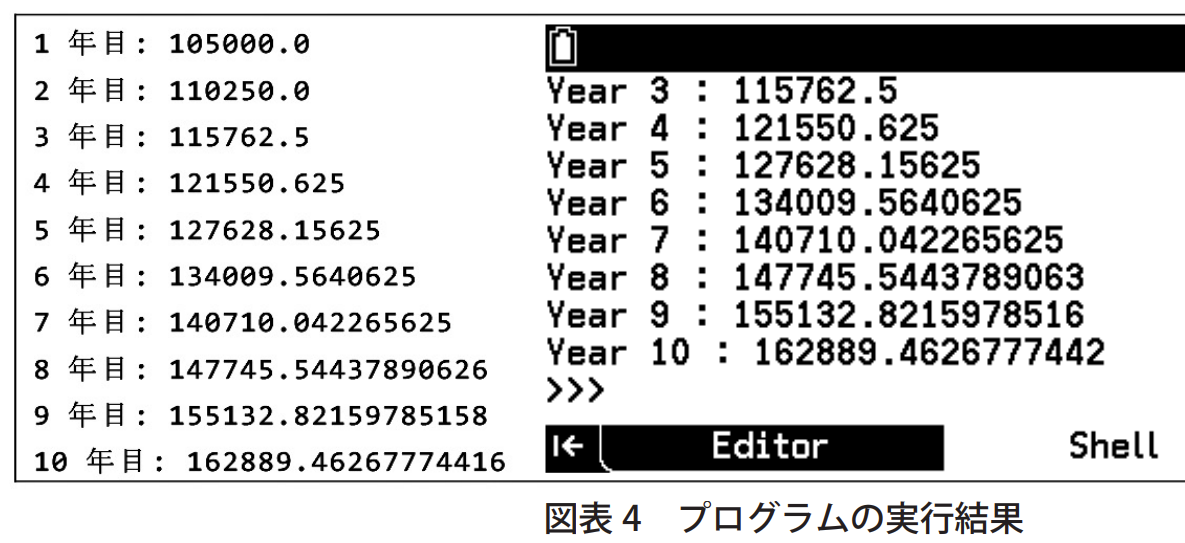
p137 図表3	▲	8年目以降の小数末尾が異なる
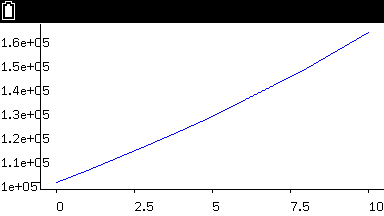
p137 図表5	△▲	タイトル・凡例・マーカー機能無し、軸目盛り設定不可
p138 図表7	△	numpyモジュールが無いためrandomモジュールで代用
p138 図表8	△	numpyモジュールが無いためrandomモジュールで代用
p139 図表10	△▲	numpyモジュールが無いためrandomモジュールで代用、タイトル・軸ラベル機能無し、棒塗り無し
p139 図表12	△	numpyモジュールが無いためrandomモジュールで代用
p140 図表13	△▲	numpyモジュールが無いためrandomモジュールで代用、matplotの色分けが使えないため、casioplotで書き直し
p145 図表2	△▲	タイトル・軸ラベル機能無し、メモリ不足で実施できないためdt=0.2で実行
p146 図表6	△▲	タイトル・軸ラベル機能無し
p147 図表8	△▲	numpyモジュールが無いためrandomモジュールで代用、タイトル・軸ラベル機能無し

スクリプト修正・結果の差異

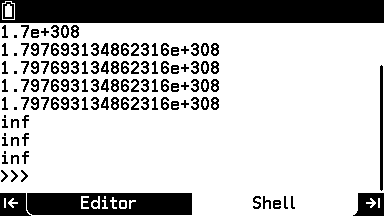
p101 図表7

• MicroPython の float型も Python と同じく倍精度浮動小数点数（64bit）である。
• ただし、 sys モジュールがないため、 sys.float_info.max で最大値を取得することはできない。
• テキストの Python では、 sys.float_info.max で取得した数値の末尾に5桁の9を並べた 1.797693134862315799999e+308 でも Inf とはならなかった。しかし、 Graph Math+ の MicroPython は先述の数値の末尾に4つ9を並べた 1.79769313486231579999e+308 でも Inf を返す。

p101.py

x = 1.7e+308
print(x)
x = 1.7976931348623157e+308
print(x)
x = 1.79769313486231579e+308
print(x)
x = 1.797693134862315799e+308
print(x)
x = 1.7976931348623157999e+308
print(x)
x = 1.79769313486231579999e+308
print(x) #inf
x = 1.797693134862315799999e+308
print(x) #inf
x = 1.8e+308
print(x)

p137 図表3

• 8年目以降は1桁上の位で丸められている。
  

p137 図表5

• グラフ描画部分は plt.plot(yokin,marker="o") plt.show() の2行のみ指定。
• markerのオプションはエラーにならないが、反映もされない。
  

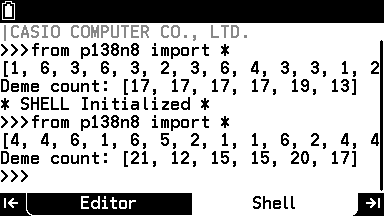
p138 図表7・8

• 出力の書式が若干異なるものの、 random モジュールで代用可能。
• numpy と random では randint の引数の与え方が異なる。
• 結果の配列表示は横一列に出力されるが、 Graph Math+ の Shell は出力行にカーソルを合わせると左右にスクロールさせることができ、結果の出力を全て閲覧できる。

p138n8.py

import random
saikoro = []
for i in range(100):
  saikoro.append(random.randint(1,6))
print(saikoro)
deme = []
for i in range(6):
  deme.append(saikoro.count(i+1))

print("Deme count:",deme)

p139 図表10

• 塗りつぶしのない棒グラフが描かれてびっくり。Graph Math+ の matplotlib は casioplot の描画関数を用いて実現しているようだが、実装の問題か、casioplotの限界なのかは調べていない。
  

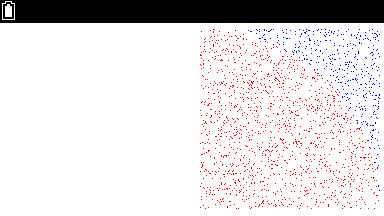
p140 図表13

• Graph Math+ の matplotlib の scatter で色分けが使えないため、 casioplot の描画関数を使うしかないと思われる。 PC の座標系は x が下に正となるので、元スクリプトのように x を上に正とするためには、引き算で反転させる必要がある。

p140n13.py

import random
import casioplot
totalcount = 2000
incount = 0
for i in range(totalcount):
  x = random.random()
  y = random.random()
  if x**2 + y**2 < 1.0:
    incount += 1
    casioplot.set_pixel(int(200+180*x),int(5+180*(1-y)),(255,0,0))
  else:
    casioplot.set_pixel(int(200+180*x),int(5+180*(1-y)),(0,0,255))
print("pi:", incount * 4.0 / totalcount)
casioplot.show_screen()

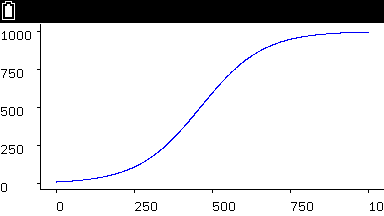
p145 図表2

• テキスト通りにやると MemoryError が出て止まってしまう。ループ回数を少なくするため、dtの値を大きく取ることに。
• 画面解像度が低いので、 dt = 0.2 としても見た目の違和感はほとんどない。
• ただし1回あたりの描画量が大きくなるので、最後の描画は x 軸を大きく下に突き抜けてしまう。最後の y[i] < 0 判定させずに range(22) と回数指定して描画したのが下のグラフだが、これでも若干下に突き抜けている。
  

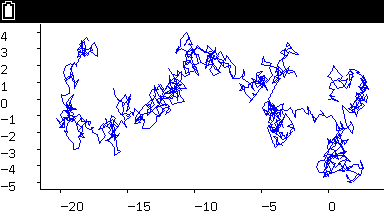
p146 図表6、p147 図表8

• p145 図表2とは違い、タイトル等が設定できないだけでテキスト通りのスクリプトで同様に動作する。
• 時間は多少かかる（図表6は約11秒、図表8は約25秒）。
  
  

今回の教材のスクリプトレベルなら意外に使えるかも

• 今回用いた教員研修用教材のスクリプトのレベルであれば、 Graph Math+ でも動くものが多かった。
• もちろん、今は Google Colab があるので、キーボードを接続したタブレット機で Google Colab に繋いだ方がモジュールの心配もなく Python を動作できるだろう（そもそも高校は一人に1台タブレット端末が使える環境を整えていたのだっけ？）。
• Graph Math+ の MicroPython に実装されている Python の関数は少ない。だが少ないからこそ CATALOG メニューで全関数を概観できる。キーボードに不慣れな生徒には、 キーが ABC 配列で、全関数を CATALOG メニューから呼び出せるグラフ電卓の Python を使うというのも一考の余地があるのかもしれない。