Go to Qiita Advent Calendar 2024 Top
LoginSignup
3
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@icchi-ioo(いっちー)

【時系列解析,Python】ARIMAモデル・Prophetモデルを利用して予測

Posted at

時系列を勉強し始めて1週間経ちました。データ分析からモデル構築・予測・評価まで、最低限できるようになったので、その一連の流れについてアウトプット。

とてもお世話になったサイト

準備するデータ

import
import pandas as pd
import numpy as np
from scipy import signal
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.seasonal import STL
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
import pmdarima as pm
from pmdarima import utils
from pmdarima import arima
from pmdarima import model_selection
from statsmodels.tsa.statespace.sarimax import SARIMAX
import optuna
from prophet import Prophet
from prophet.diagnostics import cross_validation
from prophet.diagnostics import performance_metrics

Airline Passengers（飛行機乗客数）のデータ(144, 1)を利用する。

url='https://www.salesanalytics.co.jp/591h' #データセットのあるURL
df=pd.read_csv(url,                      #読み込むデータのURL
               index_col='Month',        #変数「Month」をインデックスに設定
               parse_dates=True)         #インデックスを日付型に設定

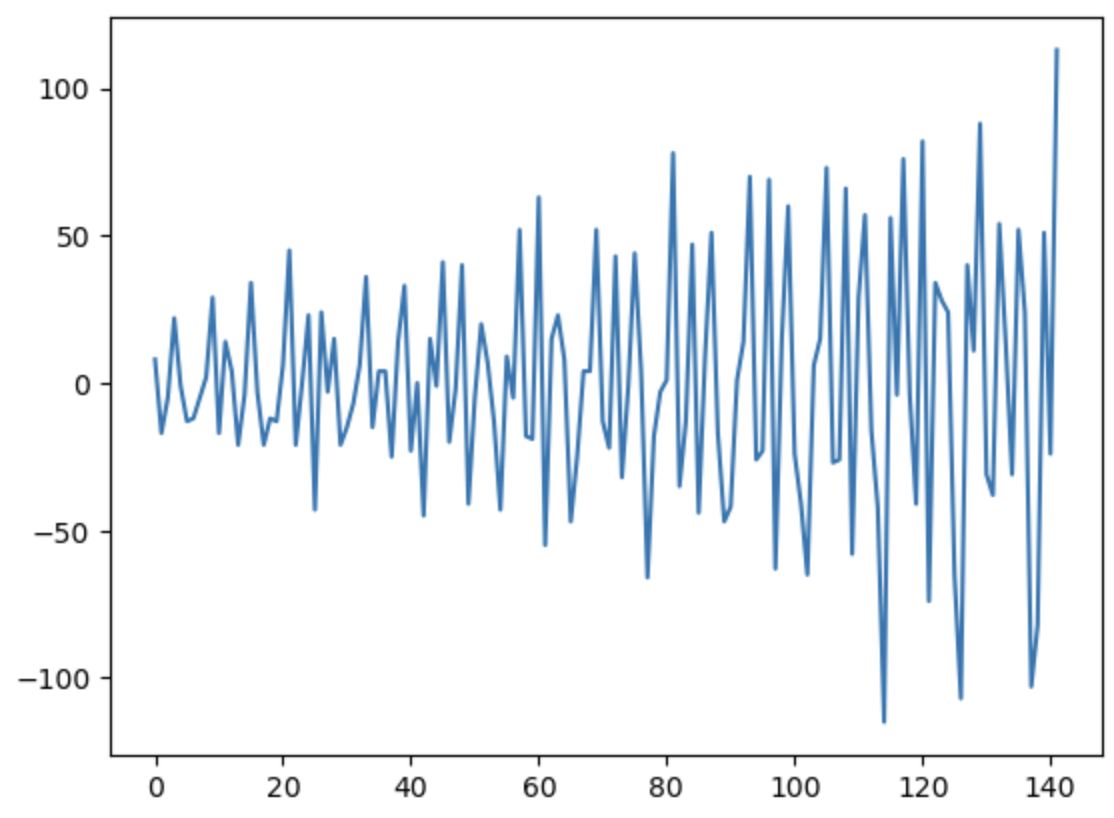
データを可視化

・　年月が経過していくにつれ分散が大きくなっている
・　上昇傾向のトレンドがある
・　季節変動があるように見える
・　周期性もあるように見える
スクリーンショット 2023-01-11 22.11.35.png

前処理の実施と定常性の有無の検定

実施する前処理

  • 1階階差
  • ２階階差
  • 対数変換
  • 対数階差
  • 季節調整

利用する検定

  • ADF検定
    • 帰無仮説：非定常データである（データは単位根を持つ）
    • 対立仮説：定常データである（データは単位根を持たない）
      単位根とは「生データでは非定常データだが、階差をとると定常データに変化するデータ」のこと。

1階階差

plt.plot(np.diff(df.Passengers))
# plt.plot(df.Passengers.diff(1)) こちらでもOK

スクリーンショット 2023-01-12 9.26.04.png
分散が時間経過に従って大きくなっていることがよくわかる。

２階階差

plt.plot(np.diff(df.Passengers, n=2))

スクリーンショット 2023-01-12 9.27.23.png
今回は１階階差と対して変わらない。

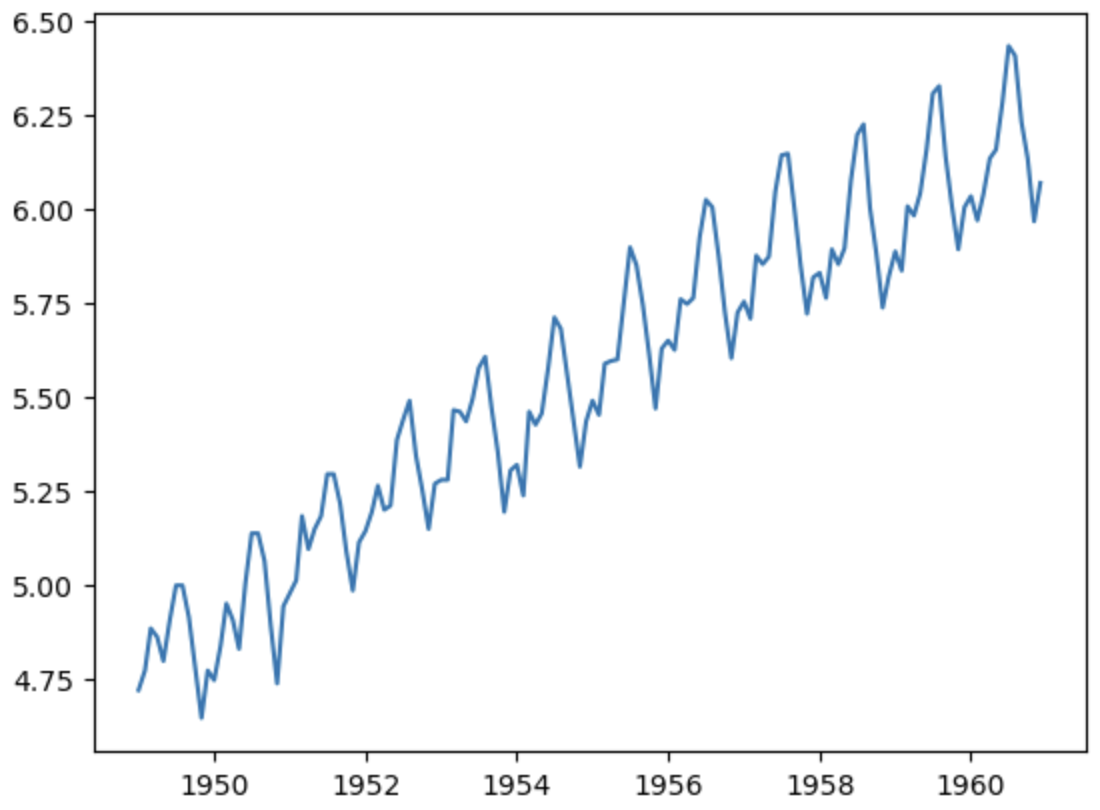
対数変換

plt.plot(np.log(df.Passengers))

スクリーンショット 2023-01-12 9.28.56.png

時間経過に伴う分散の拡大が抑えられてように見える

検定

ADF
# 対数を取ったものにADF検定（原系列）
dftest = adfuller(np.log(df.Passengers))
print('ADF Statistic: %f' % dftest[0]) #検定統計量の表示
print('p-value: %f' % dftest[1])

p-value:0.422367と帰無仮説（非定常データである）を棄却できない。

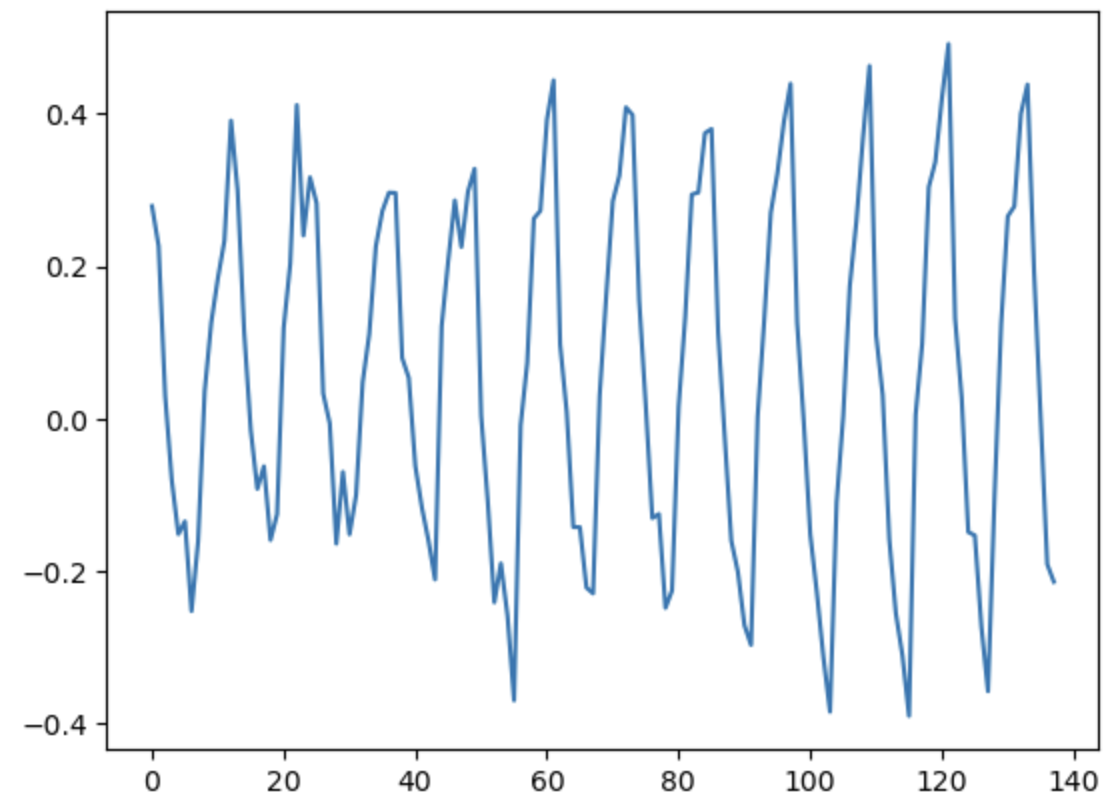
対数階差

対数1階階差
plt.plot(np.diff(np.log(df.Passengers)))

スクリーンショット 2023-01-12 9.30.03.png
平均・分散が時間とともに変化していないように見えるが、季節性の周期性があるように見えるので、おそらく共分散は時間と共に変化しており、定常過程ではなさそう。

検定

ADF
# 対数変換後、階差をとったものにADF検定
dftest = adfuller(np.diff(np.log(df.Passengers)))
print('ADF Statistic: %f' % dftest[0])
print('p-value: %f' % dftest[1])

p-value:0.071121。

対数２階階差
plt.plot(np.diff(np.log(df.Passengers), n=2))

スクリーンショット 2023-01-12 9.37.01.png
１階階差より、より定常に見えないこともないが、あまり１階階差と変わらない。だが、下記のADF検定を確認するとどうやら定常性を満たしている。

検定

ADF
dftest = adfuller(np.diff(np.log(df.Passengers),n=2))
print('ADF Statistic: %f' % dftest[0]) #検定統計量を表示させる
print('p-value: %f' % dftest[1])
print('Critical values :') 
for k, v in dftest[4].items(): #1%,5%,10%信頼区間を表示させている
    print('\t', k, v)

p-value:0.000000と定常性を満たしている。

季節調整（対数変換済み）

周期(p)をいくつか試し、グラフを確認する。

p=6
data = np.log(df.Passengers)
plt.plot(data.diff(6))
plt.show()

スクリーンショット 2023-01-12 9.40.37.png
むしろ周期性を取り出してしまったように見える。

p=12
data = np.log(df.Passengers)
plt.plot(data.diff(12))
plt.show()

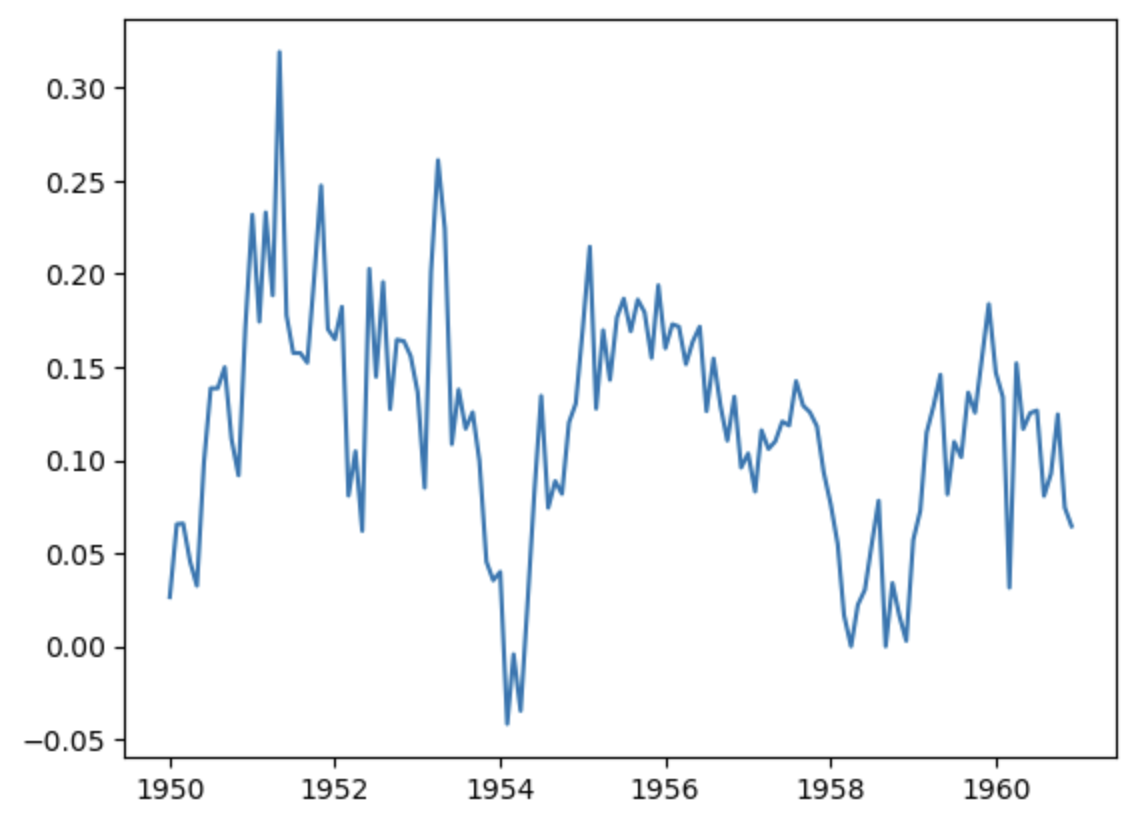
スクリーンショット 2023-01-12 9.43.10.png
飛行機への搭乗客数は年単位で周期しているように思えるので、12ヶ月の周期を取ったこのデータはおそらく季節性を除去しているはず。

検定

ADF
# 対数化後、階差数列化後、季節階差を除いたものにADF検定
dftest = adfuller(pd.DataFrame(np.diff(np.log(df.Passengers))).diff(12).dropna())
print('p-value: %f' % dftest[1])

p-value:0.000249と定常性を満たしていると言える。

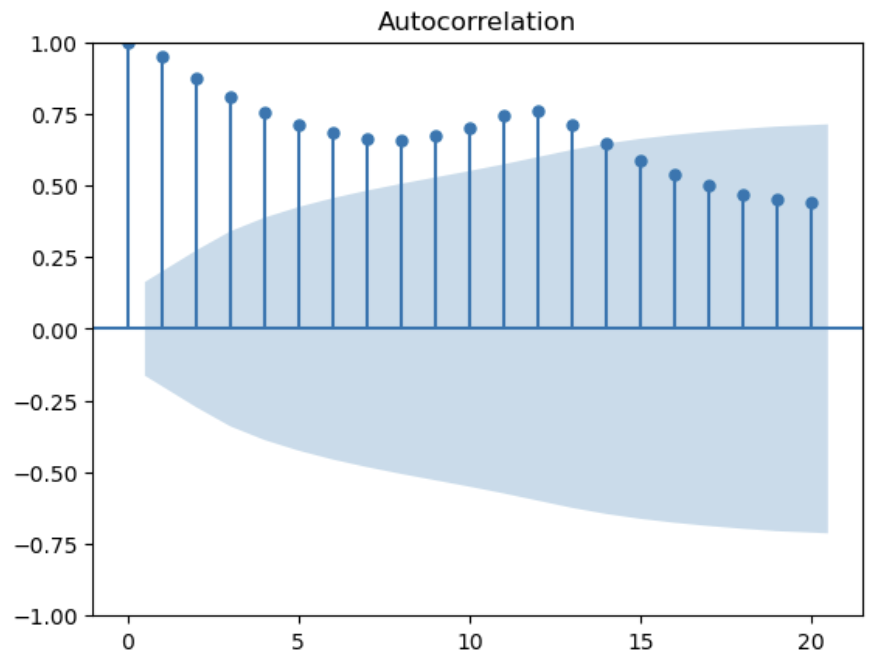
自己相関（ACF）と偏相関（PACF）

原系列と前処理後の２つのACFとPACFを比べる。

# 原系列
plot_acf(df.Passengers, lags=20)
plot_pacf(df.Passengers, lags=20)

スクリーンショット 2023-01-12 10.03.41.png
スクリーンショット 2023-01-12 10.03.48.png

# 対数化後、階差数列化後、季節階差を除いたもの
syori_dt = pd.DataFrame(np.diff(np.log(df.Passengers))).diff(12).dropna()
acf = plot_acf(syori_dt, lags=20)
pacf = plot_pacf(syori_dt, lags=20)

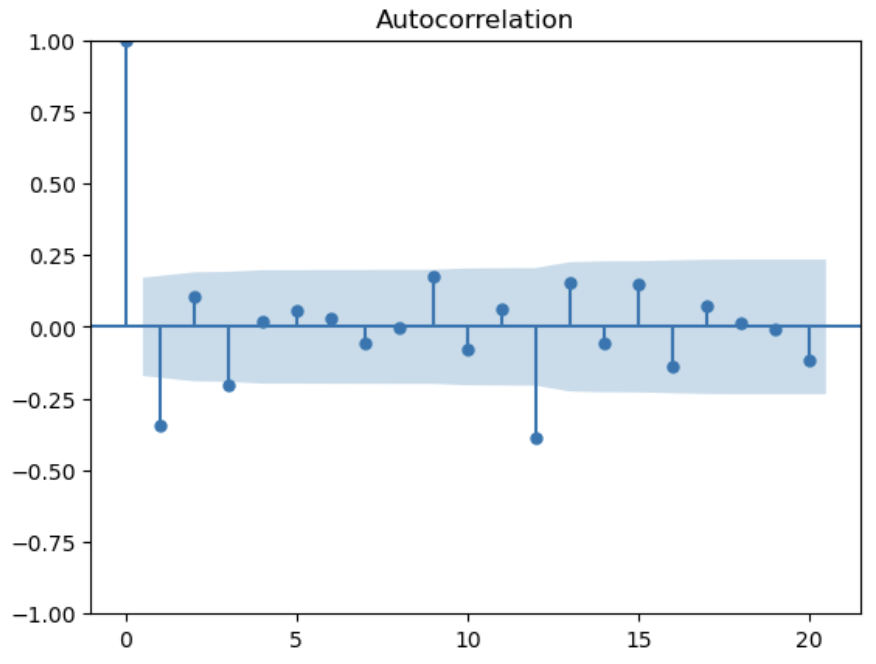
スクリーンショット 2023-01-12 10.06.21.png
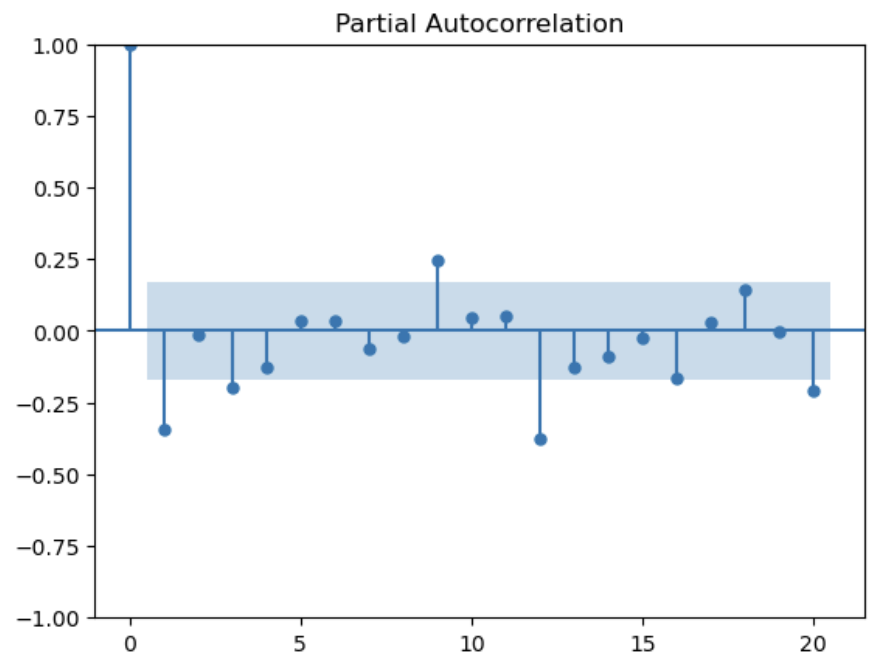
スクリーンショット 2023-01-12 10.06.27.png
処理後はACFもPACFもホワイトノイズのコレログラムに近い形をしている。

ARIMAモデルとは

ARIMA(Auto Regressive Integrated Moving Average)とはARMAモデルに階差（I）を加えたもの。非定常データの予測に活用できる。

y_t = \sum_{i=1}^{p} \alpha_{i} y_{t-i} + \Delta^d + \epsilon_t - \sum_{i=1}^{q} \beta_{i} \epsilon_{t-i}

AR（自己回帰過程）とd階階差とMA（移動平均過程）の３つの和で表現される。

ここで(p,d,q)はこの数式の次数を増やすハイパーパラメータであり、分析者が調整できる変数。次数を増やすほど、複雑な形をした時系列データを近似できるが、過剰適合するリスクもある。

ARIMAモデルのパラメータを自動推定

ARIMAモデルのパラメータであるp,d,qを自動で探索してくれるモジュールを利用する。ここでは上記パラメータ以外に季節調整パラメータについても探索させている。モデルの評価にはAICを利用。

arima_model = pm.auto_arima(train, 
                            seasonal=True,
                            m=12,
                            trace=True,
                            n_jobs=-1,
                            maxiter=10)

AIC

AIC = -2(最大対数尤度　- 推定したパラメータの数)

モデルに組み込む変数の数を増やすほど、尤度関数は複雑なモデルを近似でき、見つけられる最大値も大きくなりやすい。一方、モデルの変数の数を増やすほど、右側の項の値が罰則項のように働き、複雑なモデルを適用するのを防ぐ。つまり、左項と右項はトレードオフの関係にある。

結果の評価指標と予測誤差

MSE(平均２乗誤差)


MSE = \frac{1}{n}\sum_{i = 1}^{n}(\hat{y} - y_{i})^2

MAE(平均絶対誤差)


MAE = \frac{1}{n}\sum{i}^{n}|\hat{y} - y_{i}|

MAPE(平均絶対パーセント誤差)

MAPE = \frac{100}{n}\sum{i}^{n}|\frac{\hat{y} - y_{i}}{y_{i}}|

ARIMAモデルのコード

arima
df_train, df_test = model_selection.train_test_split(df, test_size=12)

# 予測
##学習データの期間の予測値
train_pred = arima_model.predict_in_sample()
##テストデータの期間の予測値
test_pred, test_pred_ci = arima_model.predict(
    n_periods=df_test.shape[0], 
    return_conf_int=True
)
# テストデータで精度検証
print('RMSE:')
print(np.sqrt(mean_squared_error(df_test, test_pred)))
print('MAE:')
print(mean_absolute_error(df_test, test_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(df_test, test_pred))

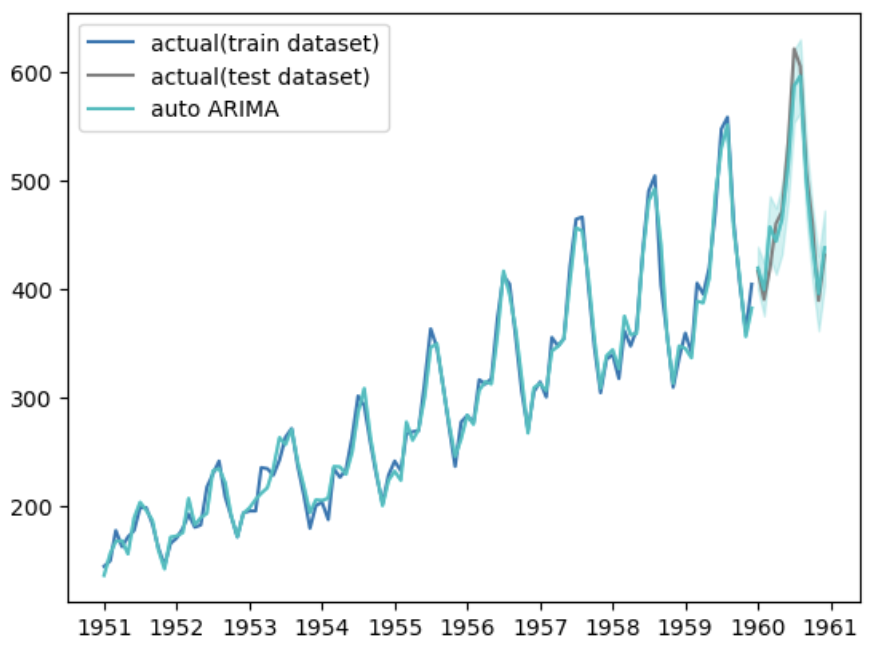
# グラフ化
fig, ax = plt.subplots()
ax.plot(df_train[24:].index, df_train[24:].values, label="actual(train dataset)")
ax.plot(df_test.index, df_test.values, label="actual(test dataset)", color="gray")
ax.plot(df_train[24:].index, train_pred[24:], color="c")
ax.plot(df_test.index, test_pred, label="auto ARIMA", color="c") 
ax.fill_between(
    df_test.index,
    test_pred_ci[:, 0],
    test_pred_ci[:, 1],
    color='c',
    alpha=.2)
ax.legend()

スクリーンショット 2023-01-12 13.15.34.png

Prophet_model

Meta(旧facebook)が開発した時系列解析用のライブラリー。時系列データを複数のトレンドと外部変数を用いて予測するモデル。

y(t) = g(t) + s(t) + h(t) + t

g(t):時系列の非周期的な変化
s(t):季節などの周期的変化
h(t):祝日休日の影響
t:誤差項

めちゃくちゃ詳しく書かれている↓

optunaでハイパラを最適化

optunaはベイズ最適化を利用。ベイズ最適化とはモデルのパラメータを調整して最適化したい指標の関数を探索すること。流れは

１、ランダムなパラメータで最適化したい評価指標を計算し、値を１つ求める。
２、１つ値が確定すると、求めたい関数はその点を通ることが確定。未探索の部分に関しても、分散と共分散を利用して求めたカーネル関数を推定する。この時推定してできた関数を獲得関数と呼ぶ。
３、次の探索点を獲得関数の平均と分散の和が大きい部分にする。以降獲得関数の再推定と探索を繰り返す。

ポイントは探索点を平均と分散の和が大きいところにしていること。平均の高いところは最適化したい指標が良い値であることを意味し、その付近に最適解が転がっていることが多い。一方分散は未知が眠っているところであり、もしかしたら、現状よりも最適な点があるかもしれない。既知情報（平均）と未知情報（分散）のバランスをとりながら探索箇所を決めているがoptunaで使われているベイズ最適化である。

optuna
def objective(trial):
    params = {'changepoint_prior_scale' : 
                 trial.suggest_uniform('changepoint_prior_scale',
                                       0.001,0.5
                                      ),
              'seasonality_prior_scale' : 
                 trial.suggest_uniform('seasonality_prior_scale',
                                       0.01,10
                                      ),
              'seasonality_mode' : 
                 trial.suggest_categorical('seasonality_mode',
                                           ['additive', 'multiplicative']
                                          ),
              'changepoint_range' : 
                  trial.suggest_discrete_uniform('changepoint_range', 
                                                 0.8, 0.95, 
                                                 0.001),
              'n_changepoints' : 
                  trial.suggest_int('n_changepoints', 
                                    20, 35),
             }
    m = Prophet(**params)
    m.fit(df_train)
    df_future = m.make_future_dataframe(periods=test_length,freq='M')
    df_pred = m.predict(df_future) 
    preds = df_pred.tail(len(df_test))
    
    val_rmse = np.sqrt(mean_squared_error(df_test.y, preds.yhat))
    return val_rmse
# ハイパーパラメータの探索の実施
study = optuna.create_study(direction="minimize")
study.optimize(objective, n_trials=100)
# 最適パラメータでモデル学習
m = Prophet(**study.best_params)
m.fit(df_train)

評価指標を比較

MSEについて

パラメータを手計算で求めたprophet:41.53
パラメータを自動で求めたARIMA:18.53
パラメータをoptuna最適化後prophet:15.27

参考サイト

3
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?