概要
・LiNGAMとは因果探索するための手法の１つ。
・因果探索とは因果ダイアグラムを発見するためのもの。
・因果ダイアグラムは下に掲載しているようなグラフで、今回の実践分析の最終目標でもある。これをpythonで出力する。
・LiNGAMのすごいところは、因果ダイアグラムの作成という人が今まで手作業でやってきたことを、客観的に数字で一意に特定できるようになったこと。
・他、因果ダイアグラム特定の手法として、ベイジアンネットワークや相関分析、CAM_UVなどがある。詳しくは、下URL参照。
コード：https://github.com/harukicode0/Causal_Discovery
LiNGAMについて
Shohei Shimizuが2006年に提唱した因果探索（Causal Discovery）のための手法。
因果探索とは因果ダイアグラムを発見すること。一方で因果推論とは因果効果の発見や効果検証を意味するので、２つは分離して考えること。
LiNGAMは4つ仮定を置くことで因果ダイアグラムを一意に特定することが可能。
LiNGAMが置いている仮定
以下の４つである。
①誤差項が非ガウス分布であること（Non-Gaussian continuous error variables (except at most one)）
②DAG（Directed Acyclic Graph：非巡回有向グラフ）である（Acyclicity）
③未観測共通潜在変数が存在しない（No hidden common causes）
④因果関係は線形和で表現可能（Linearity）
それぞれの仮定について説明する。
①誤差項が非ガウス分布であること
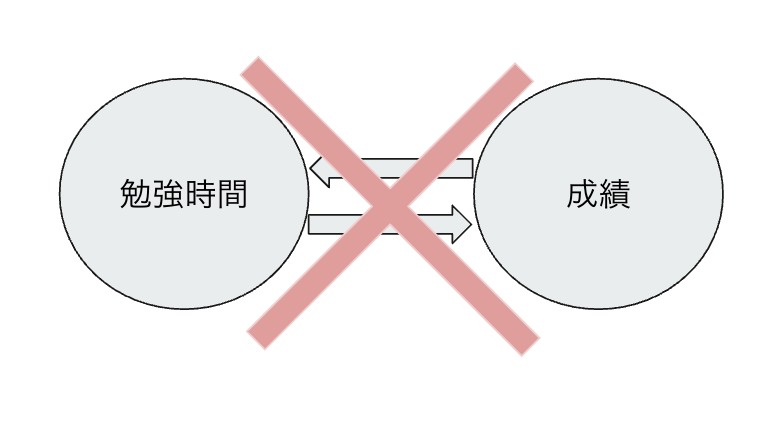
勉強時間と成績の関係について考える。今回想定するのは下図。
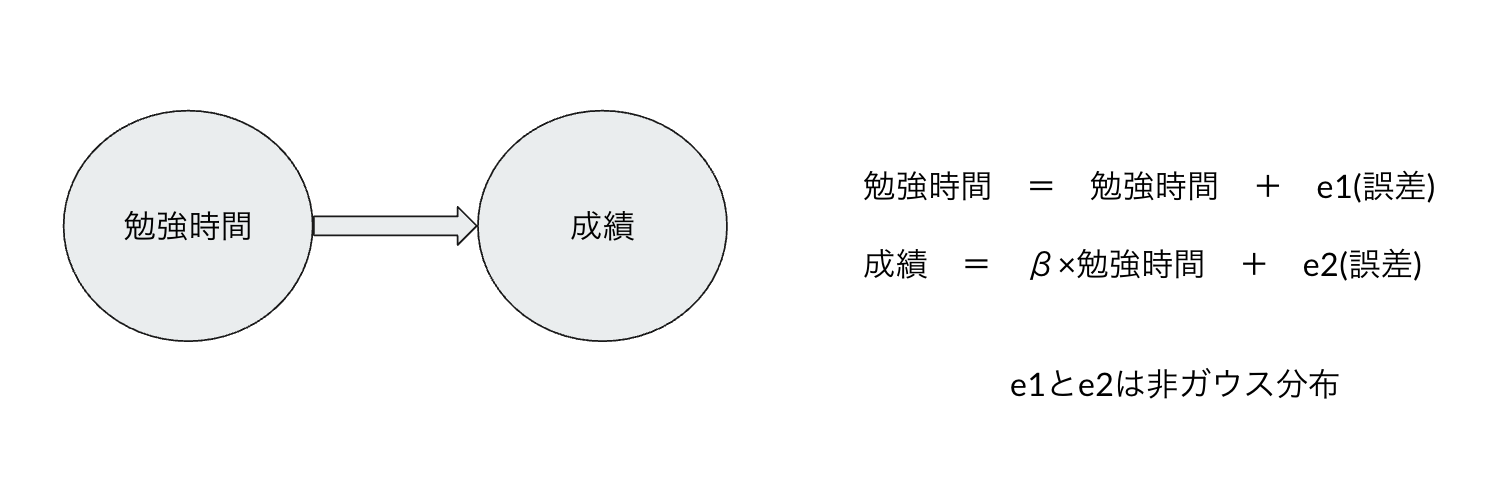
この仮定を置くと、因果ダイアグラムの矢印の方向が識別可能になる。
誤差項が非ガウス（正規分布ではない）であるとなぜ因果の方向を識別可能なのか
x１とx２の関係について考える。
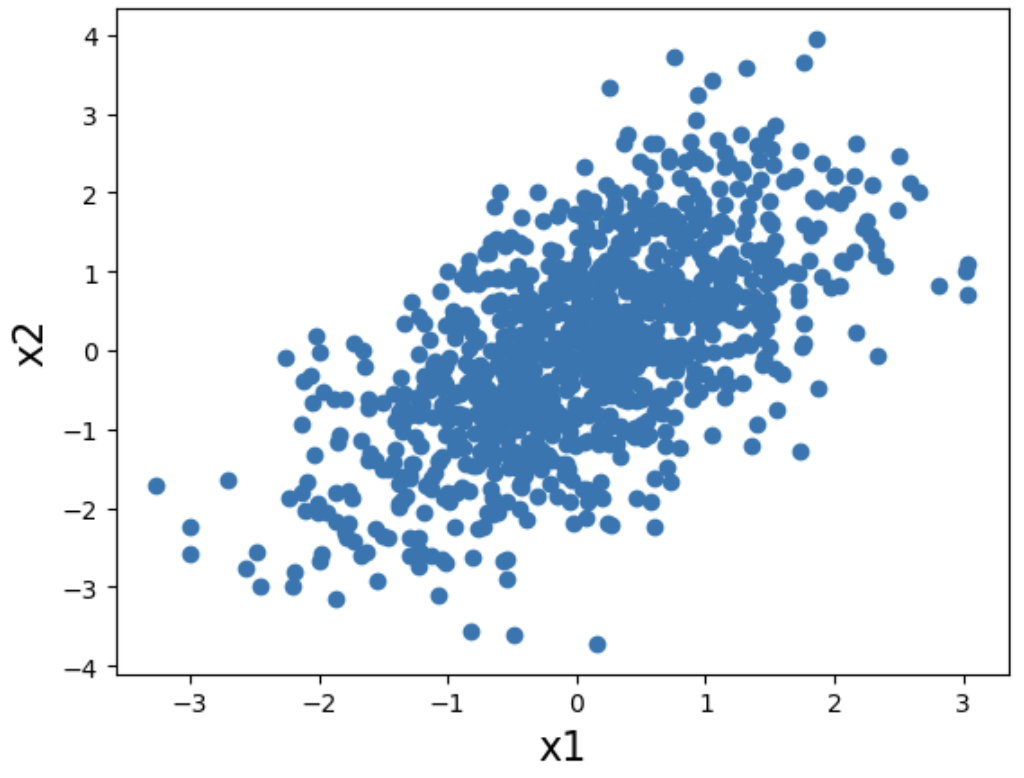
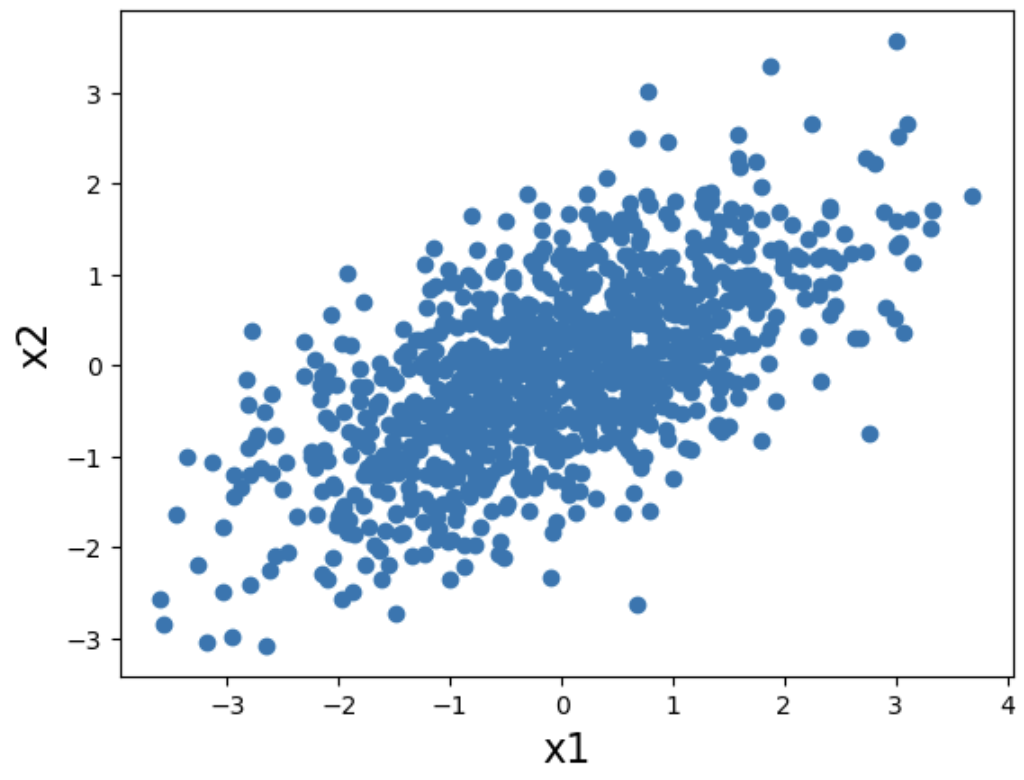
①誤差が正規分布である場合
２つの因果ダイアグラムを考える。
x１が誤差で与えられ、x２がx１×0.8と誤差の和で表現できるもの、つまりx１→x２。
x２が誤差で与えられ、x１がx２×0.8と誤差の和で表現できるもの、つまりx２→x１。
それぞれの散布図を確認して、因果ダイアグラムが識別可能かどうか確認する。
x1 = np.random.normal(0,1,1000)
x2 = x1 * 0.8 + np.random.normal(0,1,1000)
plt.xlabel('x1', fontsize = 16)
plt.ylabel('x2', fontsize = 16)
plt.scatter(x1,x2)
x2 = np.random.normal(0,1,1000)
x1 = x2 * 0.8 + np.random.normal(0,1,1000)
plt.xlabel('x1', fontsize = 16)
plt.ylabel('x2', fontsize = 16)
plt.scatter(x1,x2)
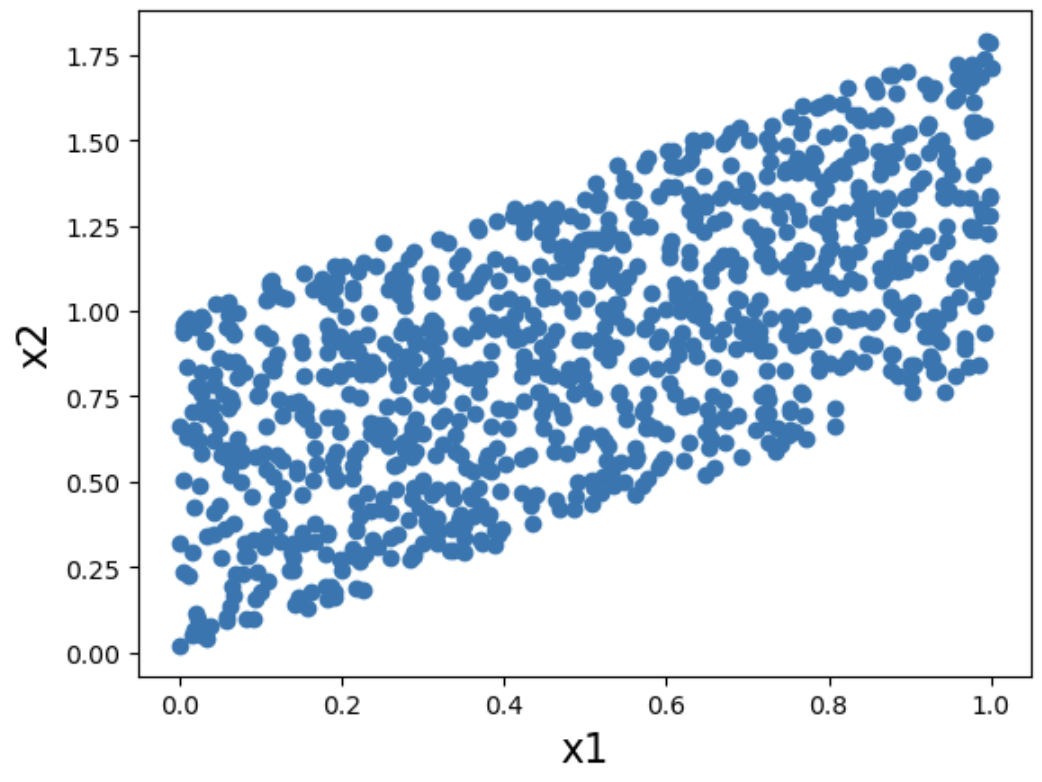
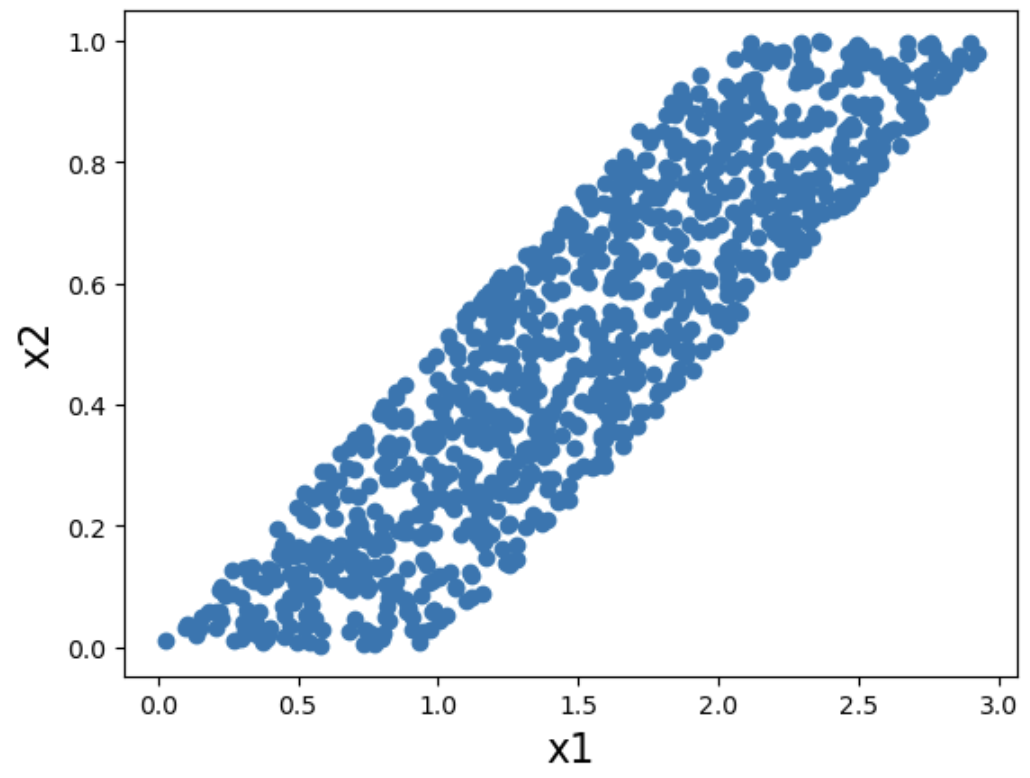
②誤差が一様分布である場合
x１とx２の散布図を確認すると、因果ダイアグラムの矢印が違うと散布図の形が違うことが確認できる。つまり、散布図から因果ダイアグラムを識別可能である。
x1→x2の因果ダイアグラムを想定した時の散布図について確認。
x1 = np.random.uniform(0,1,1000)
x2 = x1 * 0.8 + np.random.uniform(0,1,1000)
plt.xlabel('x1', fontsize = 16)
plt.ylabel('x2', fontsize = 16)
plt.scatter(x1,x2)
x2 = np.random.uniform(0,1,1000)
x1 = x2 * 2 + np.random.uniform(0,1,1000)
plt.xlabel('x1', fontsize = 16)
plt.ylabel('x2', fontsize = 16)
plt.scatter(x1,x2)
②DAG（Directed Acyclic Graph：非巡回有向グラフ）である
DAGとは因果の矢印が一方通行であり、変数から流れた効果はその変数に２度と戻らない構造のこと。
下図はDAGではないことの例。勉強時間が増えると成績が上がり、成績が上がるとモチベーションが高まり、さらに勉強時間が増えるというループが発生している構造。このような構造は因果が逆流しているのでDAGとは言えない。
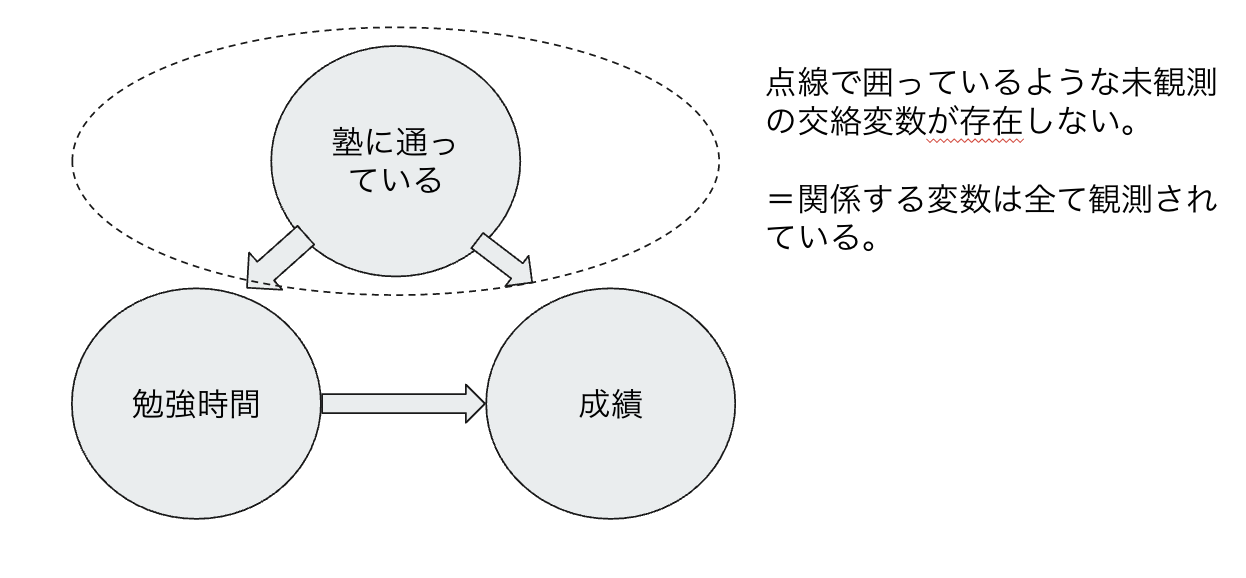
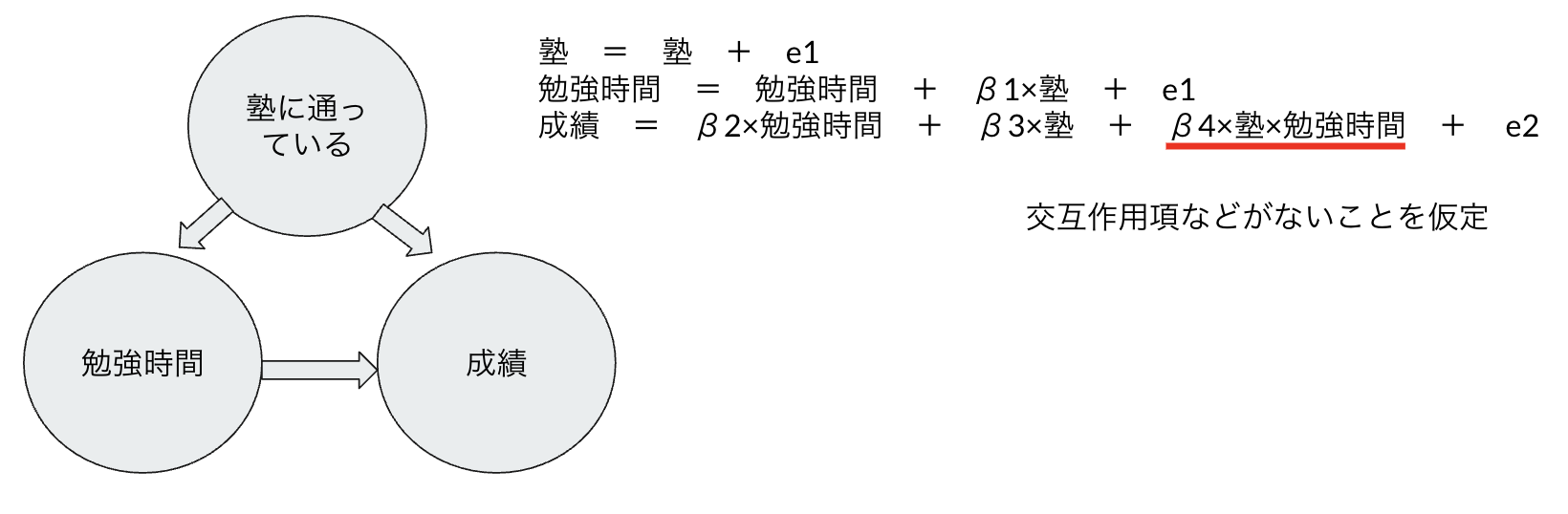
③未観測共通潜在変数が存在しない
LiNGAMでは因果に関係する変数は全て観測されていることを前提としている。下図のような、点線で囲まれた未観測の影響する変数が存在しないこと。
④因果関係は線形和で表現可能
つまり、因果関係は１次式で表現可能であることを想定している。交互作用や２次関数などの非線形な項は存在しないことを仮定している。
LiNGAMの仕組み
大まかな流れを説明する。詳しくは他サイトを確認。
①独立主成分分析(ICA)を実施。
②①の結果出てきた行列の対角成分が０になるように調整。
③所定の数まで行列の中の０の数を増やす。この時、０にするのは絶対値の小さいもの。
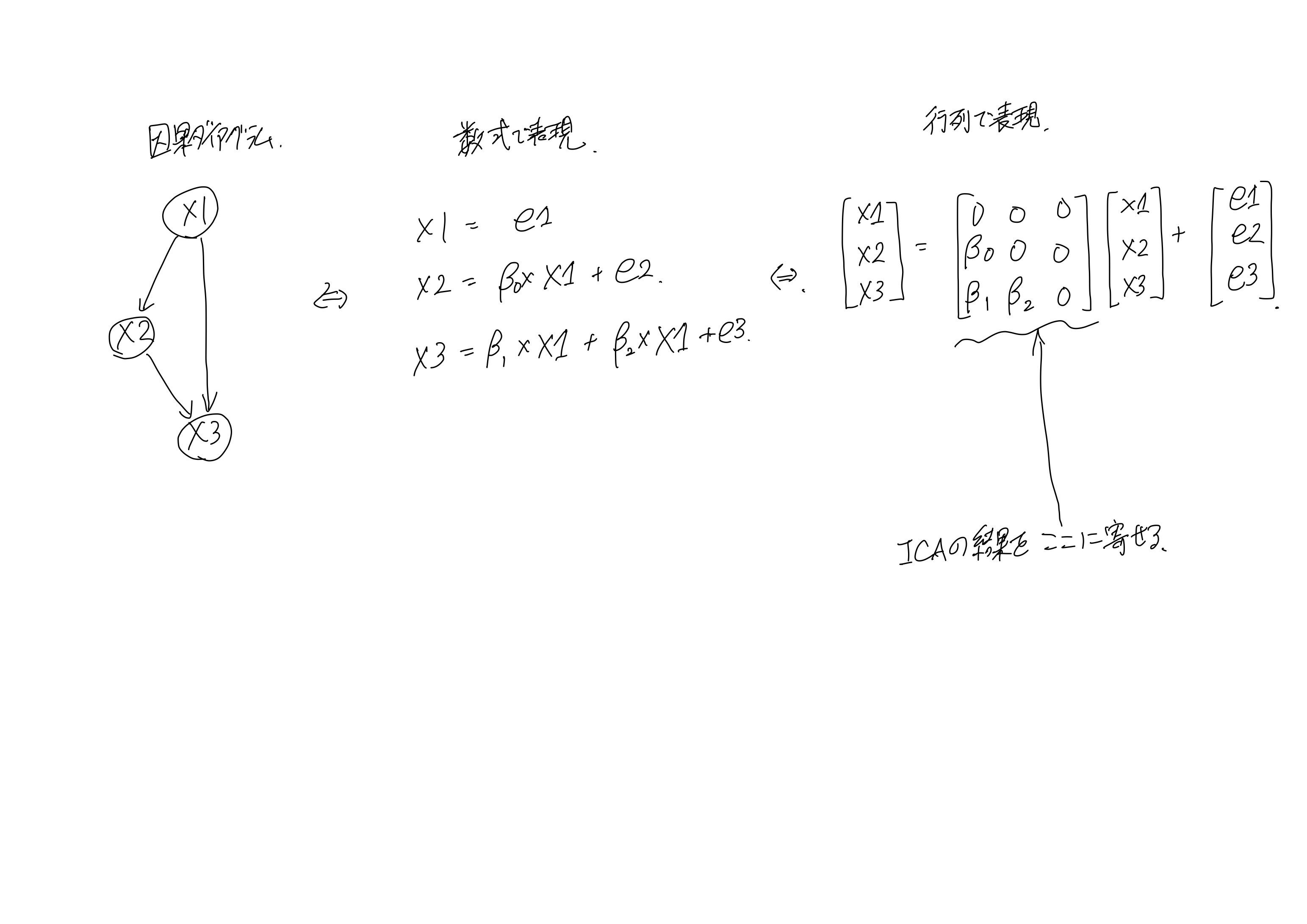
さらに大雑把に説明すると、ICAで出てきた行列をごちゃごちゃいじって、因果ダイアグラムを作成する。以下①②ではICAのイメージと、行列で因果ダイアグラムを表現する方法について説明し、LiNGAMの頭と尻尾のイメージについて持ってもらう。
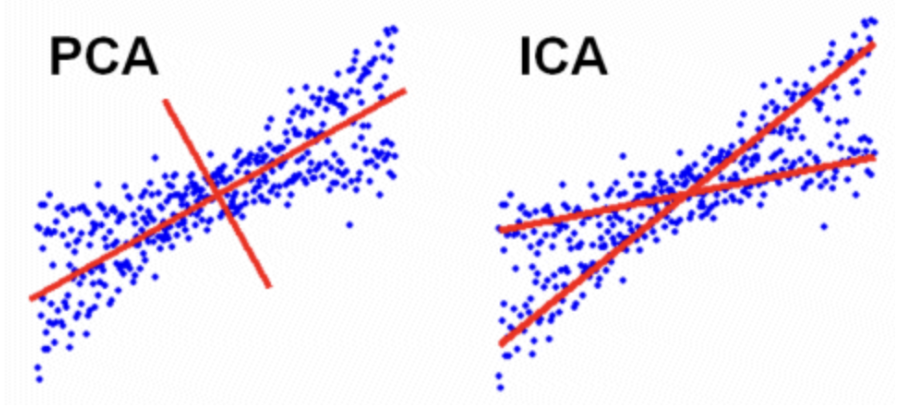
①ICAのイメージ
ICAとはデータに新たに軸を引き直す作業において、各軸（各独立主成分）同士の相関が０、かつ、独立になるように操作したもの。
２次元平面におけるPCA（主成分分析）とICAの幾何学的イメージが下図。ICAは軸が第１主成分に直交するのではなく、自由に決定できるというイメージ。
②行列で因果ダイアグラムを表現
因果ダイアグラムは行列で表現できる。
ここで注目すべき点は対角成分が０であること、０が多いこと。
以下の２つを理解するとLiNGAMのイメージがしやすい。
・０になると変数同士の関係を断ち切れること
・対角成分の下三角形のところ数字が０ではないと因果の下流に変数があること
シミュレーション
以下の２つシチュエーションで各メソッドのシミュレーションする。
①未観測共通変数が存在しない場合
②未観測共通変数が存在する場合
シミュレーションするメソッドは４つ。
・DirectLiNGAM
・BottomUpParceLiNGAM（未観測変数が存在しても良いLiNGAM）
・CAM-UV（因果の途中経路に未観測変数が存在する場合）
・ベイジアンネットワーク
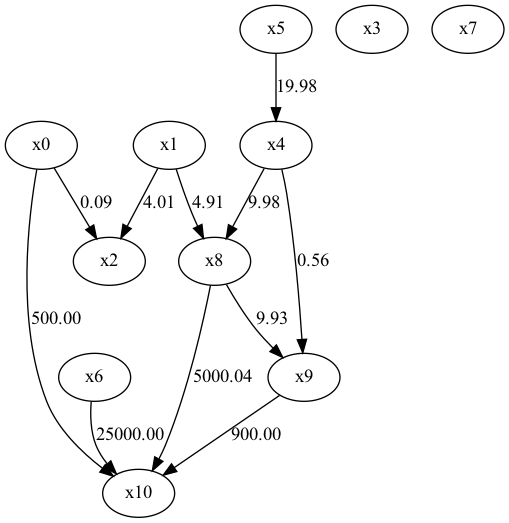
以下はデータ数８００で、各シチュエーションで各メソッドでシミュレーションした時の結果を掲載している。
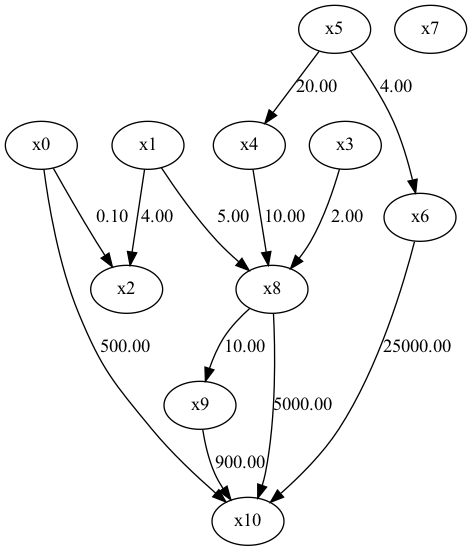
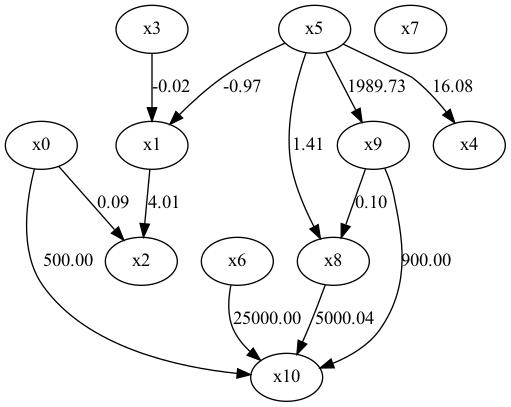
①未観測共通変数が存在しない場合
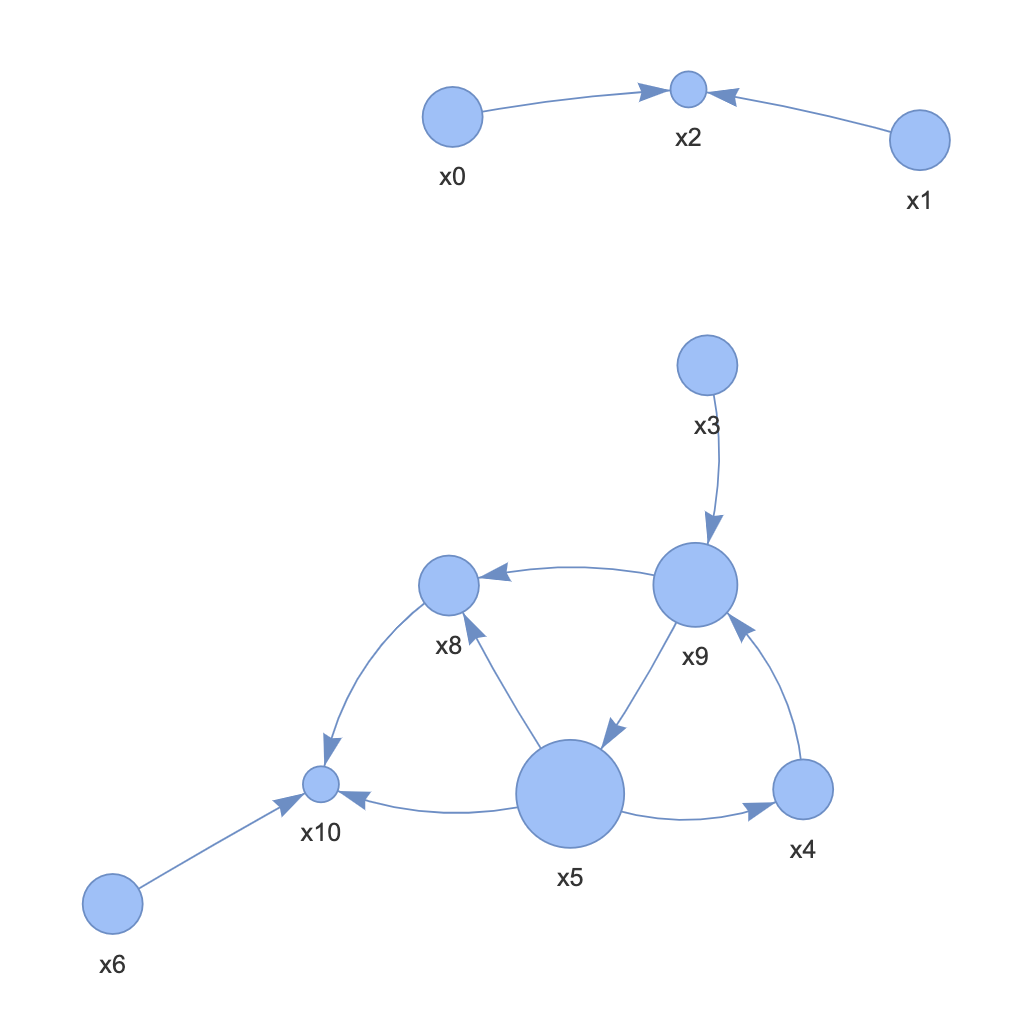
正解の因果ダイアグラム
x７は関係のないノイズを表現している。
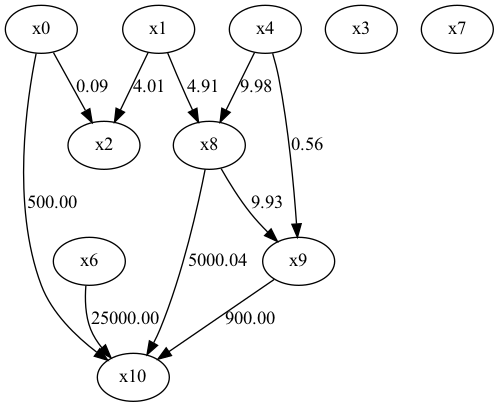
結論はDirectLiNGAMが最も正解に近い構造をシミュレーションしている。
・DirectLiNGAM
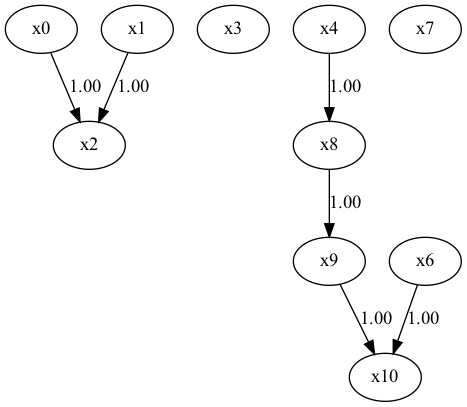
・BottomUpParceLiNGAM（未観測変数が存在しても良いLiNGAM）
・CAM-UV（因果の途中経路に未観測変数が存在する場合）
・ベイジアンネットワーク
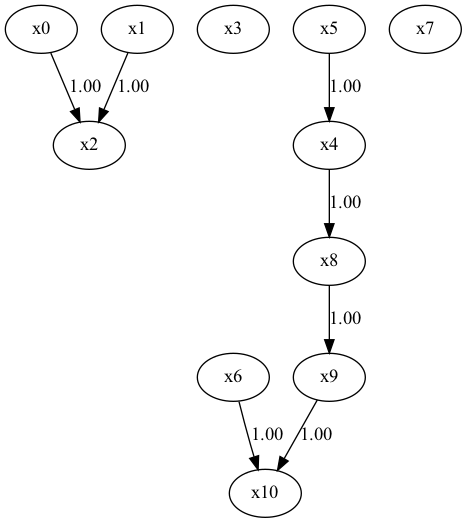
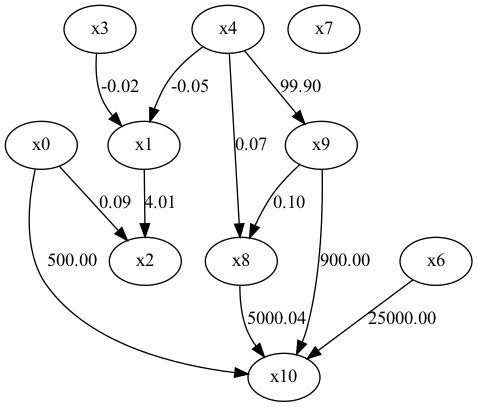
②未観測共通変数が存在する場合
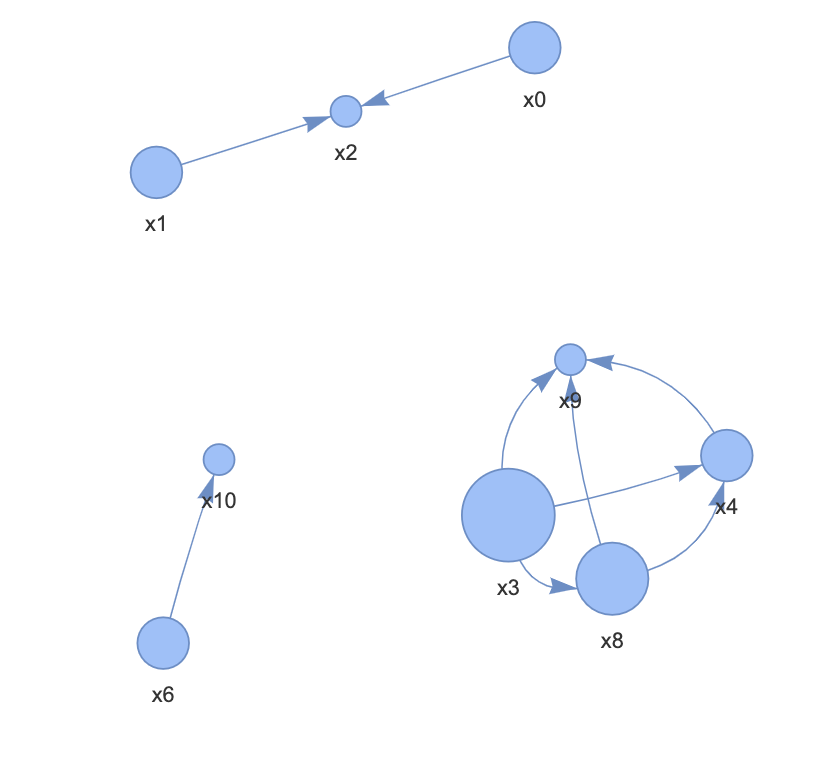
正解の因果ダイアグラム。
x５を未観測共通変数としている。
DirectLiNGAMが最も因果構造を正しく推定している。
・DirectLiNGAM
・BottomUpParceLiNGAM（未観測変数が存在しても良いLiNGAM）
・CAM-UV（因果の途中経路に未観測変数が存在する場合）
・ベイジアンネットワーク
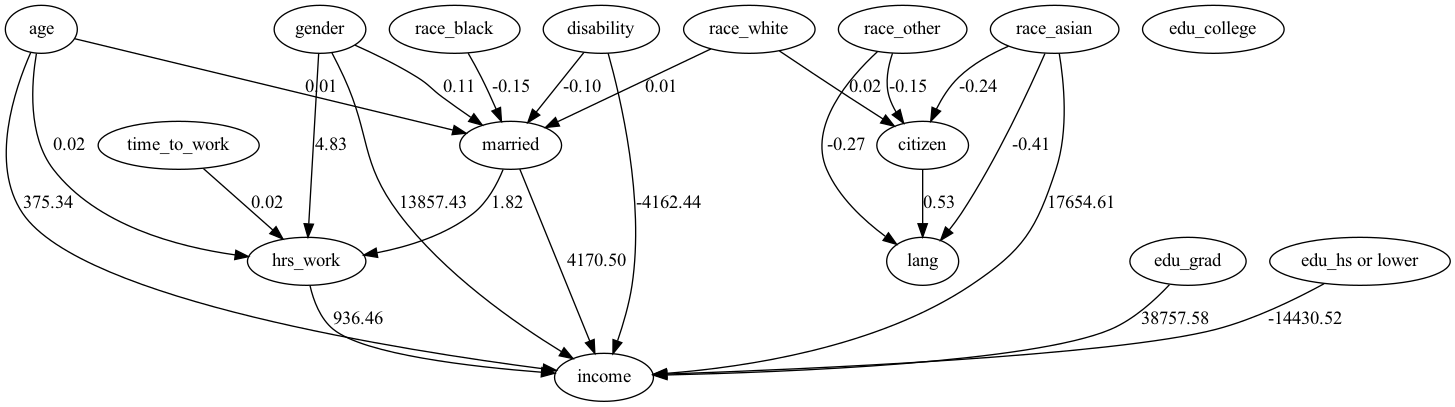
以上よりDirectLiNGAMを利用して因果構造を推定する。
今回利用する実データ
American Community Survey 2012を利用する。
このデータはアメリカの個人の属性データと年収を調査したもの。
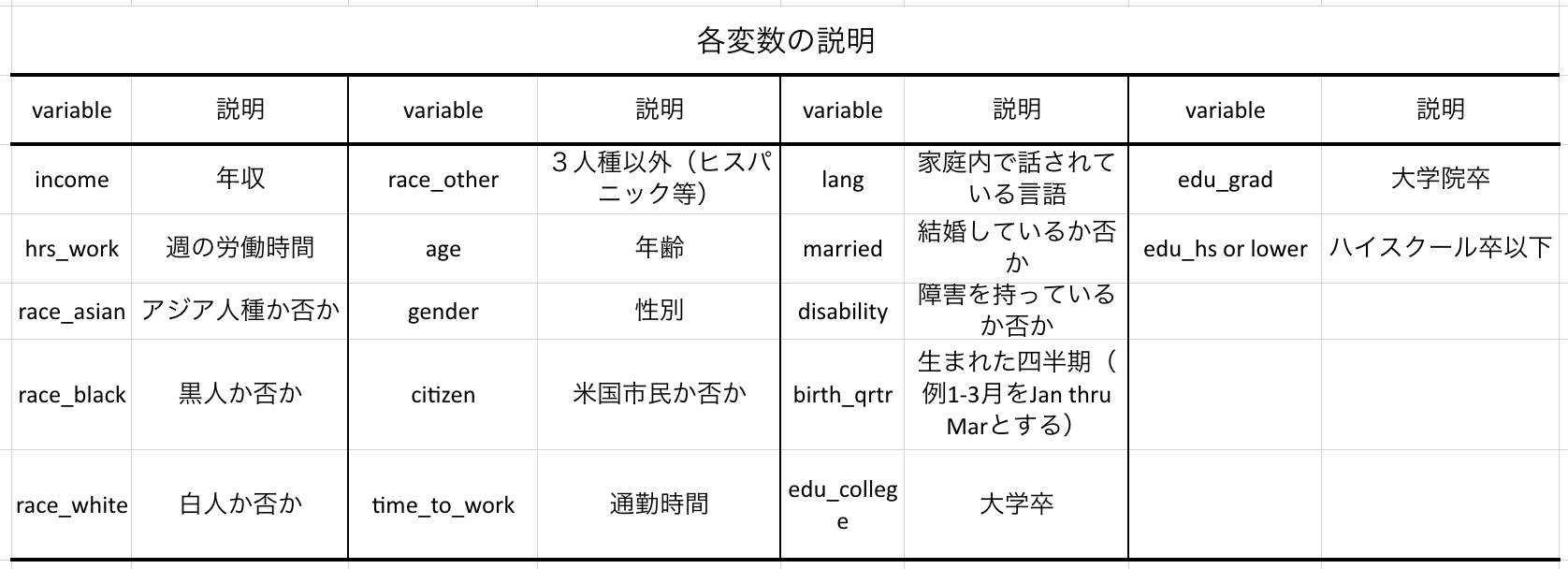
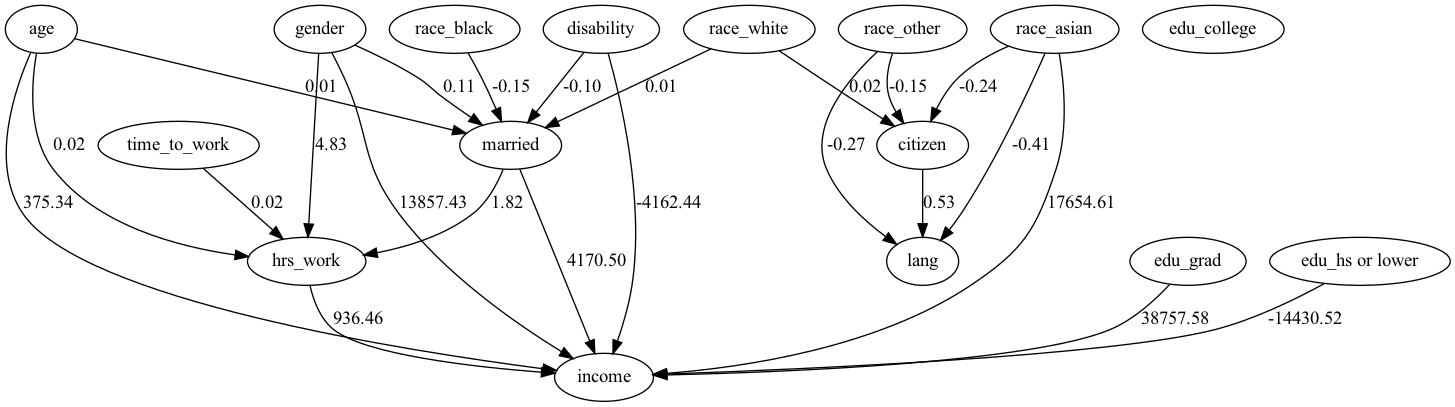
分析に使うデータは下表を確認。行った前処理としてはダミー変数化と欠損値のある行の削除、欠損値の多いカラムの削除。
結果と解釈
概ね先行研究で示された結果が確認できた。
見方を少しだけ確認する
・年齢が１つ上がるごとに平均＋３７５ドルの影響がある。
・週の労働時間が１時間増えると年収が平均＋９３６ドルの影響がある
・男性の方が女性よりも平均＋１.３万ドル稼ぐ
といったことがわかる。
この結果に１点気になる点がある。それはアジア系であることが年収に対して平均＋１.７万ドルの影響があること。このことについて検証する。
アジア人であることが年収に影響を与えるのか〜交差項について検証
先行研究を調べた結果、アジア系であることが年収に正の影響があることに対して、様々な仮説を立てることができる。
仮説１：裕福なアジア系が世界１の国を目指して移住してくるから？
→検証するためには移民の資産や収入等について調査が必要。アジア系２世代の収入の確認も必要。
仮説２：アジア系は学業努力を惜しまない文化・コミュニティを持っており、アジア系は高学歴。Explaining Asian Americans’ academic advantage over whites（Amy Hsin and Yu Xie,2014）
→交互作用を検証すれば、何らかの知見を得られそう。手元データからも実施できる。検証するにはコミュニティや文化が学業努力に与える影響について調査すること。
仮説３：高収入（エンジニア、金融、医者等の専門職）についている傾向がある。
→検証するためには職業についての調査が必要。
仮説４：アジア系は物価の高いところに住みがち？（https://www.washingtonpost.com/news/wonk/wp/2016/12/29/the-asian-american-advantage-that-is-actually-an-illusion/）
結論としてはアジア系であることが直接高収入に繋がるというわけではなさそう。今回、仮説２に関しては手元データから検証できそうなので、実施する。
収入に対する学歴と人種の交互作用を検証
目的はアジア系であることの効果を調べること。
結論は手元のデータから確度の高いことは何も言えない。
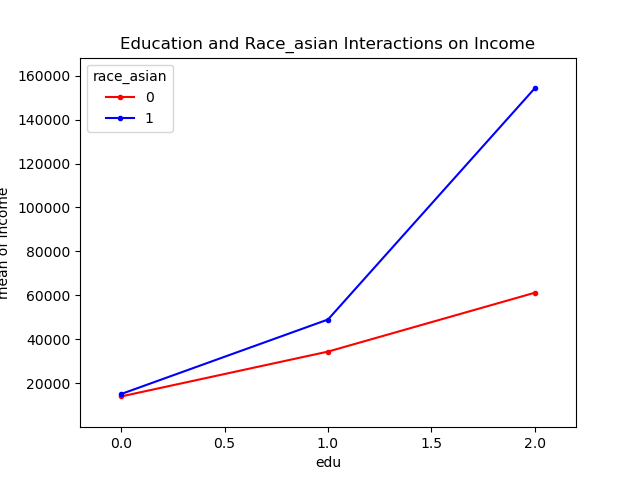
目的を調査するために、アジア系で、かつ高学歴である場合は他の人種よりも稼ぎやすいかどうか交互作用検証し、アジア系であることの特異性を発見する。
検証した結果が下グラフ。下グラフより交互作用があることがわかる。
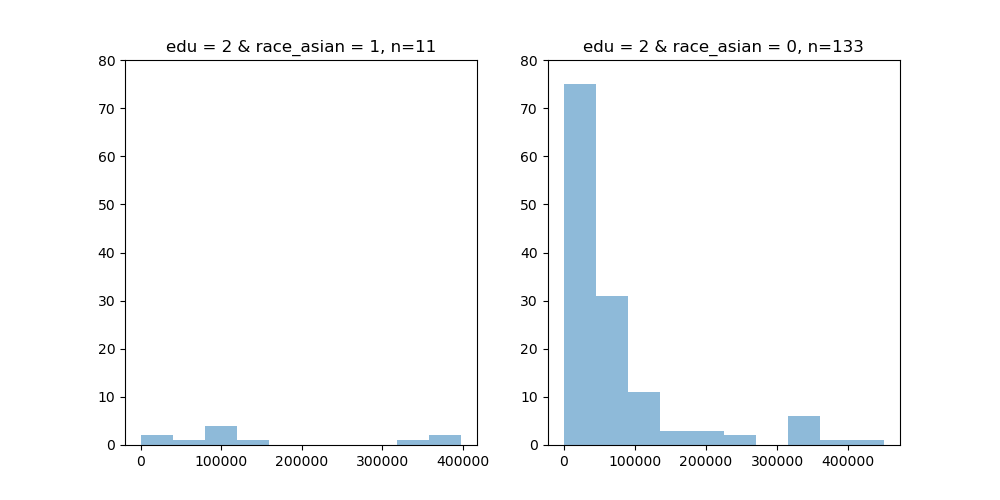
これより、高学歴なアジア系が年収を急激に上げていることがわかるが、念の為、高学歴におけるアジア系か否かの別で見た年収のヒストグラムを確認する。
すると、アジア系である場合のデータ数が１１と少なく、外れ値に影響されやすいことがわかった。結論としては、このデータからでは妥当性のあることは何も言えないことがわかる。
LiNGAMの弱点
今回使用したLiNGAMの弱点を下記
・LiNGAMは未観測共通潜在変数について仮定しないので、今回年収の原因を考えるにあたって当たり前に考えなければならない共変量「能力」や「モチベーション」、「職業」などの交絡変数について考慮していないこと。ただし、BottomUpParceLiNGAMやCAM-UVは考慮している。
・線形和の因果関係を扱うので、交互作用について考慮していない。
・ループが発生するような因果関係についても考慮できない。
あくまで、データさえあれば因果ダイアグラムを数値で客観的に特定できる手法というだけで（未知なデータに対しても実行できるので十分すごい）、因果関係を確実に特定できるものではないことに注意したい。
また、LiNGAMで因果ダイアグラムを特定するには、因果関係があると考えられているデータを観測者が仮定した上で収集する必要がある。
参考文献
つくりながら学ぶ! Pythonによる因果分析 ~因果推論・因果探索の実践入門 (Compass Data Science)