目的
グラフ理論について、なかなか理解できなかったのですが、
つてつちさんのYoutubeの動画がかなりわかりやすかったので、Qiitaでアウトプットしようと思います。
参照
下記のつてつちさんの動画を参照させていただきました。わかりやすい動画を作成していただき、ありがとうございます。
グラフ理論とは?
グラフ理論は、関数や統計グラフなどではなく、下記のような頂点と線の2つで関係性を表したもの。

グラフ理論で嬉しいこと
最適解を求めるものによくグラフ理論は利用されています。
例えば、Google Mapで目的地までの行き方を調べられると思いますが、そういうときにも利用されています。
また、マーケティングなどでお客さんが次に何を購入するかを推測してレコメンドをするためにも利用されています。
意外とグラフ理論の考え方は、身近に使われています。
今回、グラフ理論の中で説明するところ
今回は、グラフ理論の中でも総当り数を求める方法について説明します。
(これ以外にも、アソシエーション分析だったり、マッチングアプリの組み合わせ候補を決めることにもグラフ理論は利用されています。)
総当たり戦の例
「あるサッカーチームが4チームありました。総当たりのリーグ戦をする場合は、全試合は何試合か?」
今回は、グラフ理論でこの問について考えてみることにします。
まず、下記のよう4チームを書きます。この点のことを、グラフ理論では頂点やノードと呼びます。

試合とは、このチーム同士が集まって1試合をすることなので、点どうしをつなげる青い線のことを試合とみなすことができます。
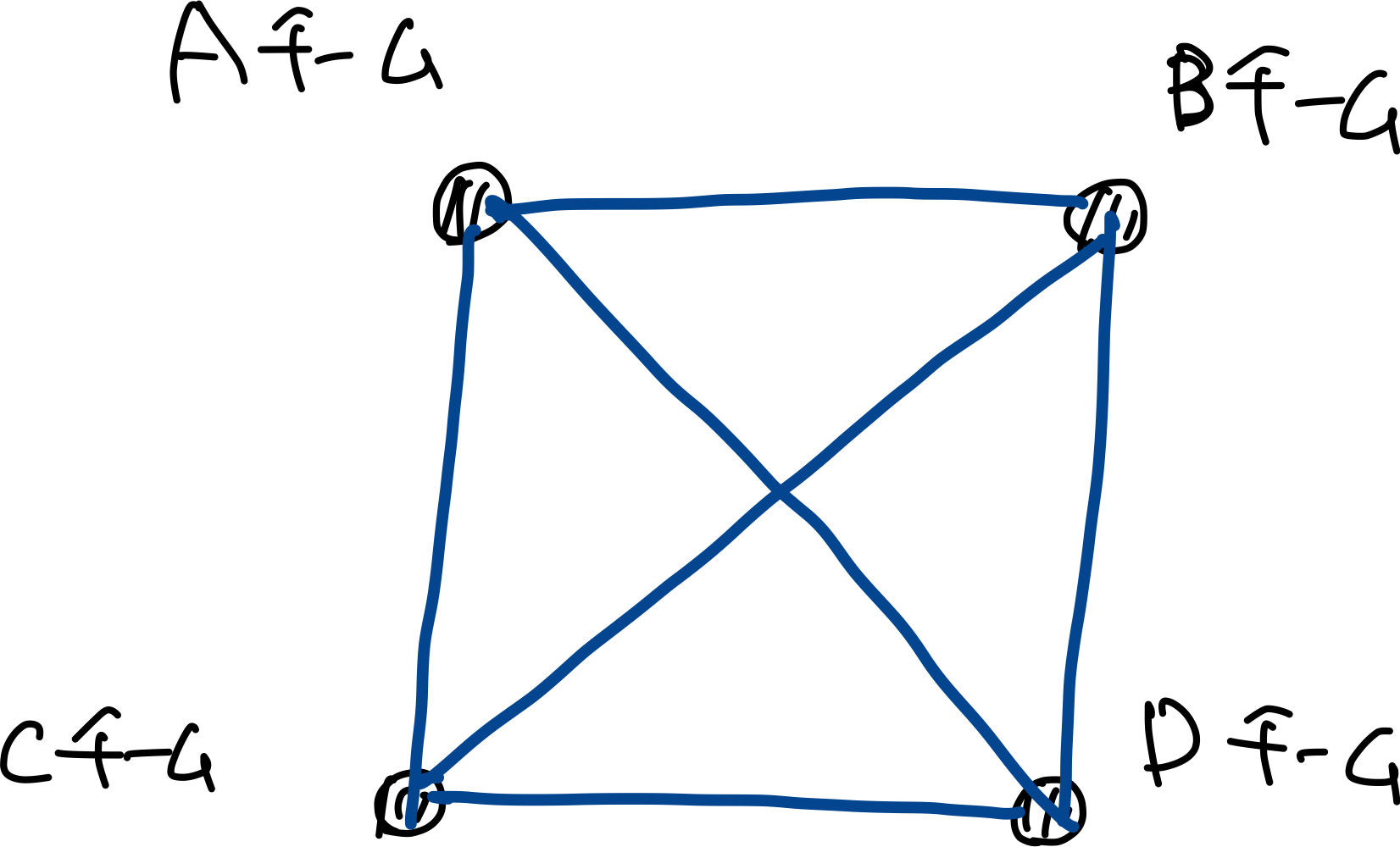
この線のことをグラフ理論では辺やエッジと呼びます。
今回、辺の数は6つになります。
「あるサッカーチームが4チームありました。総当たりのリーグ戦をする場合は、全試合は何試合か?」
よって、この問の答えは6試合となります。
このようにグラフ理論は使われています。
こちらを抽象化した下記のお題にもグラフ理論は適用できます。
「あるチームがnチームありました。総当たりのリーグ戦をする場合は、全試合は何試合か?」
Nチームの場合
一つのチームから出てくる辺の数は、n-1本になります。
チーム数はNチームです。
なので、
合計の試合数= n(n-1) / 2
と表すことができます。(n(n-1)だと、線を2回数えてしまうために、2で割ります。)
最適な日数
グラフ理論を用いることで、こんな問にも答えることができます。
「サッカーチームが5チームあり、総当たりのリーグ戦は最短で何日か?」
これがグラフ理論が最適化に使われている理由になります。
こちらはすでにグラフ理論で証明されており、
nが奇数のときは、 n日
nが偶数のときは、n-1日です。
よって、今回のチーム数は5つなので、5日になります。(詳しくはつてつちさんの動画を見てください。)
まとめ
グラフ理論では、amazonのレコメンドや最短経路を求めるのにもよく利用されているものなので、より深く学んでいこうと思います。(知識が増え次第、更新していきます)