前回に続いて今回は ADALINE アルゴリズムによるデータ分類を行っていきたいと思います。
前回のパーセプトロンアルゴリズムはこちらからご覧ください。
ADALINEとは
まず前回のパーセプトロンがどのようなものだったか、図でわかりやすく説明すると
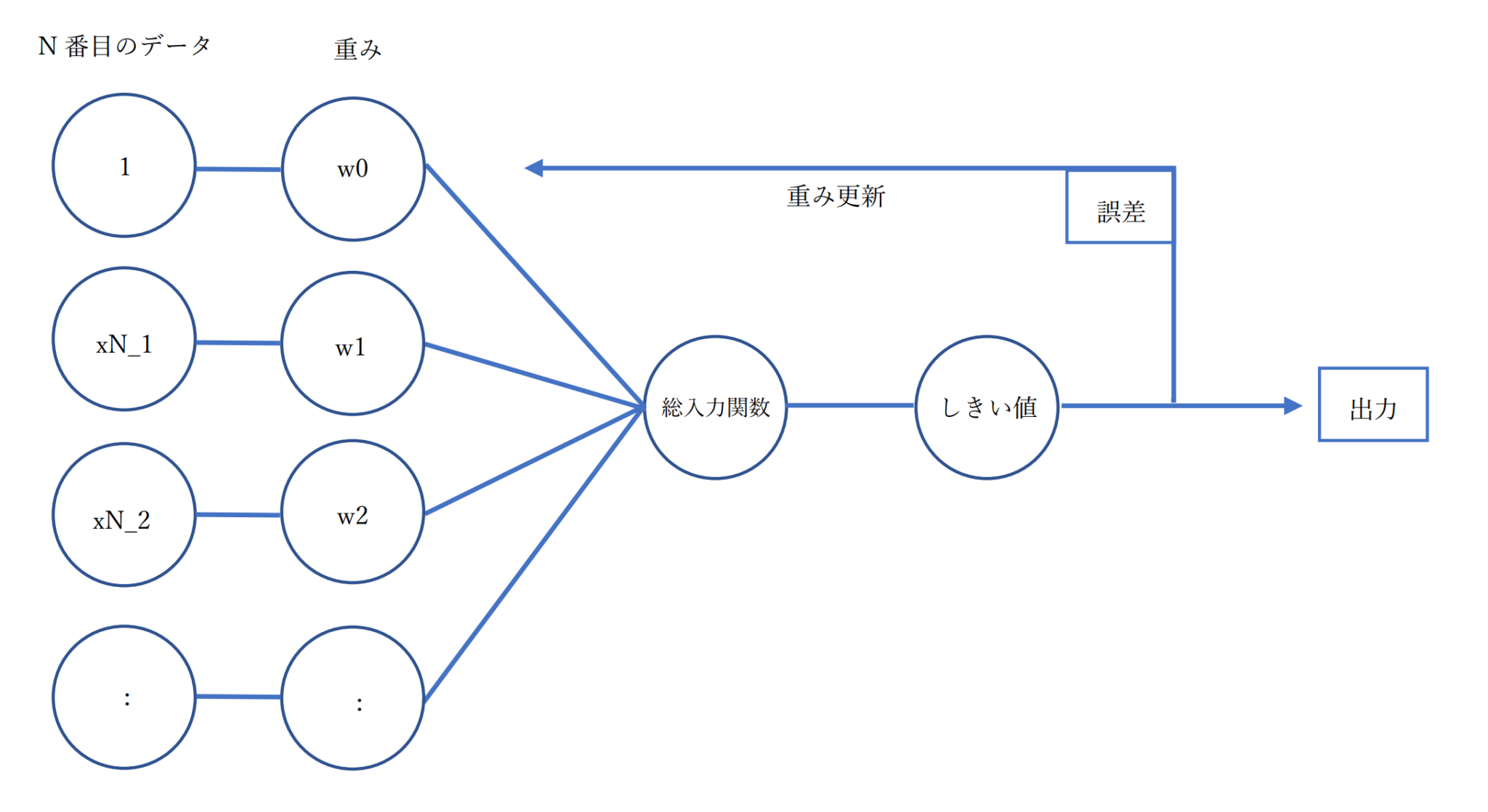
このように、訓練データごとに「(特徴量×重み)の総和」をしきい値に通してクラスラベルを予測しては答え合わせをして、誤差があれば重みを修正するといったものでした。
では結論、ADALINEとは何かというと、パーセプトロンアルゴリズムの改良バージョンです。
なにが改良かというと、重みの更新方法に違いがあります。
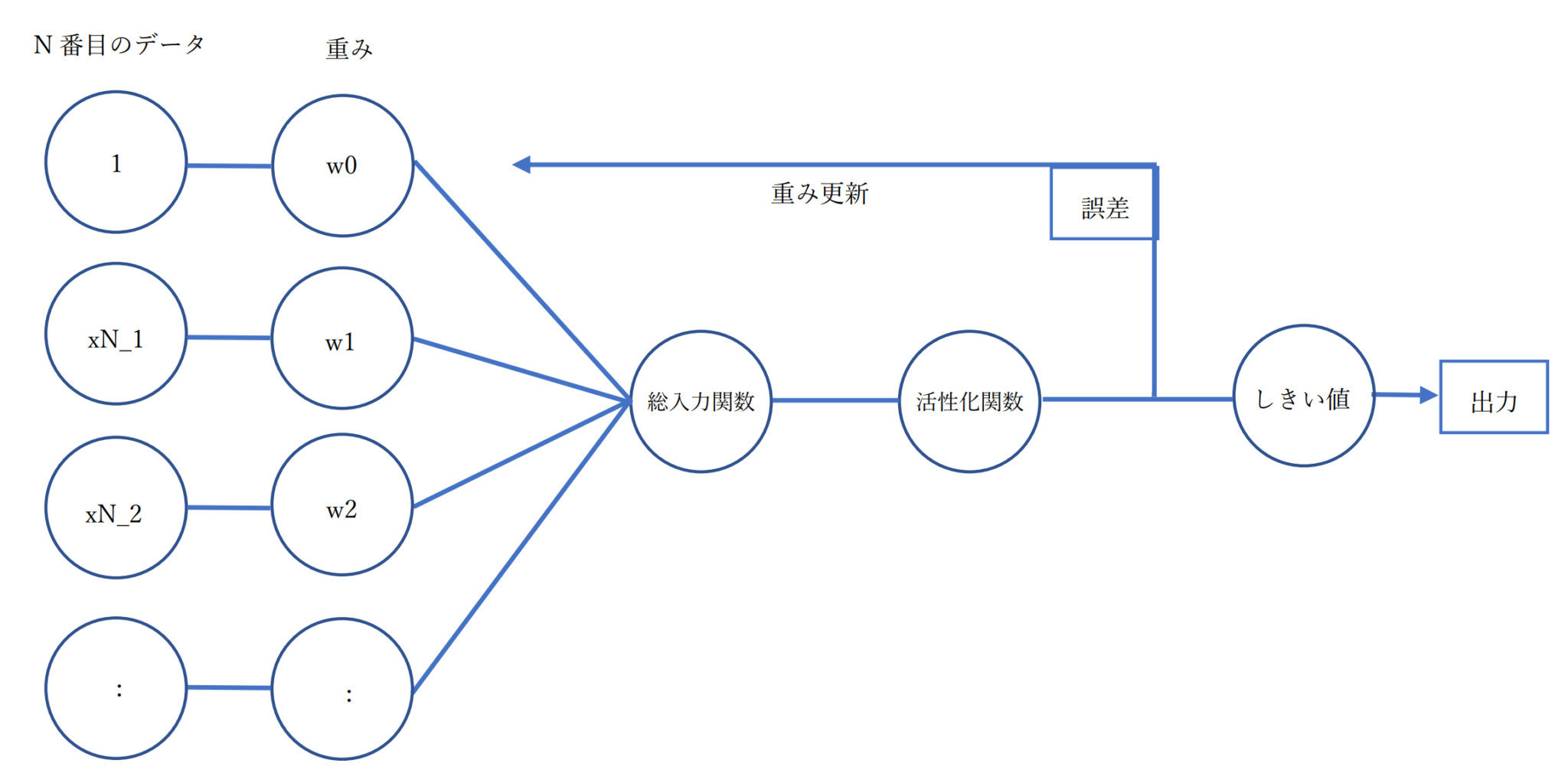
上の図がADALINEアルゴリズムによる分類の流れです。活性化関数は総入力の恒等関数なので、特に何かしているというわけではありません。
注目したいのはしきい値を通す前に誤差を評価しているというところです。
つまり、ADALINEではただしきい値を正しくくぐり抜けて、正しいクラスラベルを予測できればそれでいいというわけではなく、できるだけ真のクラスラベルとの誤差ができるだけ小さくなるように調節してから、最後にしきい値でクラスラベルを予測するのです。
また、パーセプトロンでは各訓練データごとに毎回重みを更新していましたが、ADALINEでは全ての訓練データセットに基づいて更新されます。
コスト関数 ・ 勾配降下法 という考え方
先ほど、ADALINEではできるだけ真のクラスラベルとの誤差ができるだけ小さくなるように調節してから、最後にしきい値でクラスラベルを予測すると述べたのですが、この誤差を計算するのがコスト関数というものです。
ADALINEでは次のような誤差平方和をコスト関数として定義します。
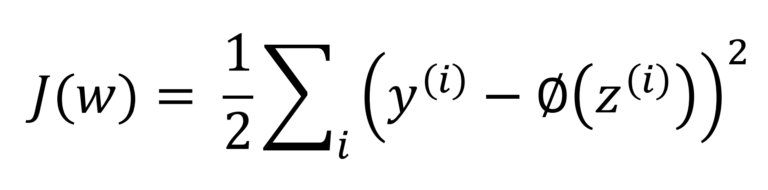
y(i)は真のクラスラベルの値で、Φ(z(i))が入力値(訓練データに重みがかかったもの)です。
1/2はコストの値をコンパクトにするために便宜上追加したものにすぎません。
いきなり式を書いてしまったのでややこしいかもしれませんが、真のクラスラベルとの差の合計を計算していることがわかるかと思います。
またもう一つの特徴として、このコスト関数が凸関数になるということです。そのため、勾配降下法を使ってコストを最小化する重みを見つけることができます。
私が勉強している本(Python機械学習プログラミング(←Amazonリンクはこちら))から図を抜粋させて頂きますと、グラフは下のようになります。
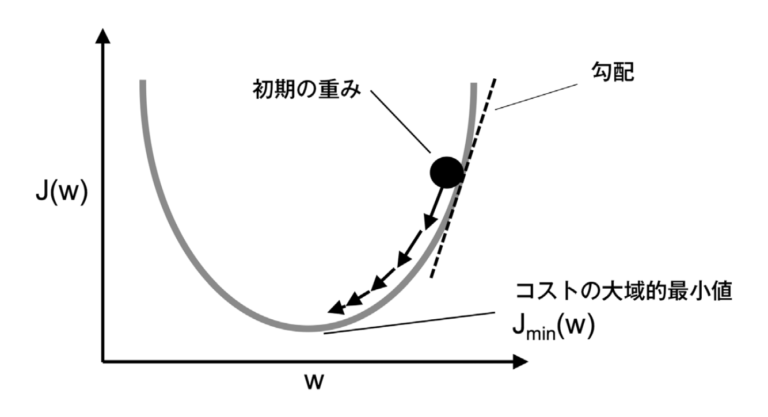
このコスト関数が最小になるまで重みの更新を繰り返すということです。
本書「Python機械学習プログラミング」では、さらに細かい計算式まで掲載されていますのでよかったら読んでみてください。
Pythonで ADALINE を実装
前回同様、筆者は以下のPythonコードをGoogleColaboratoryで実行しました。GoogleColaboratoryは環境構築が必要ないので便利です。
また、訓練データもネットから引っ張ってくるので用意する必要がありません。
今回も、2種類の花合計100枚を機械学習によって種類を区別し、結果を表示させようと思います。
ADALINE の実装
class AdalineGD(object):
"""ADALINE分類器
パラメータ
------------
eta : float
学習率(0.0 < eta <= 1.0)
n_iter : int
訓練データの訓練回数
random_state : int
重みを初期化するための乱数シード
属性
-----------
w_ : 1次元配列
適合後の重み
cost_ : リスト
各エポックでの誤差平方和のコスト関数
(エポックは訓練そのもののこと)
"""
def __init__(self, eta=0.01, n_iter=50, random_state=1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
""" 訓練メソッド
パラメータ
----------
X : {配列のようなデータ構造}, shape = [n_examples, n_features]
訓練データ
n_examplesは訓練データの個数
n_featuresは特徴量の個数
y : array-like, shape = [n_examples]
目的変数
戻り値
-------
self : object
"""
# NumPyの乱数生成器rgenを生成
rgen = np.random.RandomState(self.random_state)
# 重みを標準偏差0.01の正規分布中の小さな乱数で初期化
self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
# コストを格納する変数
self.cost_ = []
# 訓練回数だけ繰り返す
for i in range(self.n_iter):
net_input = self.net_input(X)
# activationメソッドは活性化関数だが、
# 分類においては入力関数の恒等関数特だから意味を持たない
# 後に学習する回帰では意味のある関数を入れることがある
output = self.activation(net_input)
# 真のクラスラベル値との誤差を計算
errors = (y - output)
# 重みw1以降の更新
self.w_[1:] += self.eta * X.T.dot(errors)
# 重みw0の更新
self.w_[0] += self.eta * errors.sum()
# コスト関数(誤差平方和)の計算
cost = (errors**2).sum() / 2.0
# コストを格納
self.cost_.append(cost)
return self
def net_input(self, X):
# 総入力を計算
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, X):
# 活性化関数だが、分類では入力値をそのまま出力
return X
def predict(self, X):
# 1ステップ後のクラスラベルを返す
return np.where(self.activation(self.net_input(X)) >= 0.0, 1, -1)
上のコード中のfor文に注目すると、パーセプトロンとは違ってfor文は一つしかありません。(パーセプトロンではfor文が2重でした。)
これは、個々の訓練データを評価する度に重みを更新するのではなく訓練データセット全体のコストを計算してから重みを更新していることを表しています。
いざ訓練
では続けて以下のコードブロックを追加して訓練を実行します。
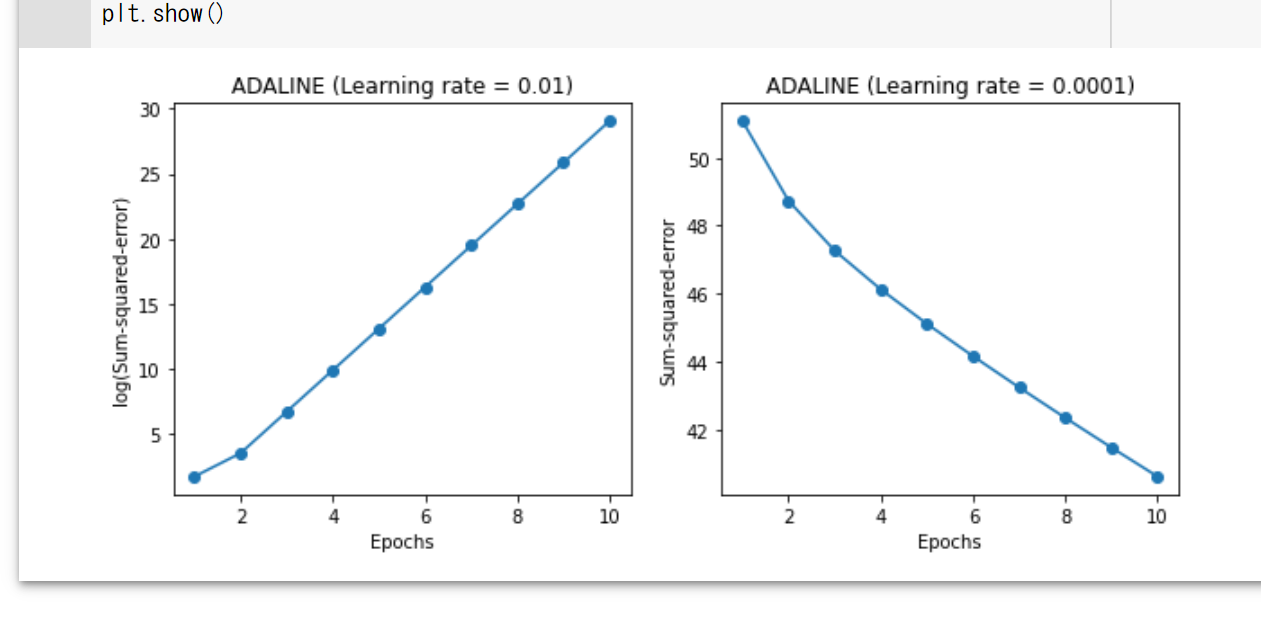
ここで試しに、学習率を0.01と0.0001の2種類で学習を行ってみます。その際、コストの変化も可視化してみます。
# 描画領域を1行2列に分割
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))
# 学習率0.01で勾配降下法によるADALINEの学習を実行
ada1 = AdalineGD(n_iter=10, eta=0.01).fit(X, y)
# エポック数とコストの変化を表すグラフのプロット
ax[0].plot(range(1, len(ada1.cost_) + 1), np.log10(ada1.cost_), marker='o')
# 軸ラベルを設定
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(Sum-squared-error)')
# タイトルの設定
ax[0].set_title('ADALINE (Learning rate = 0.01)')
# 学習率0.0001で勾配降下法によるADALINEの学習を実行
ada2 = AdalineGD(n_iter=10, eta=0.0001).fit(X, y)
# 同様にエポック数とコストの変化を表すグラフを生成
ax[1].plot(range(1, len(ada2.cost_) + 1), ada2.cost_, marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Sum-squared-error')
ax[1].set_title('ADALINE (Learning rate = 0.0001)')
# グラフを表示
plt.show()
見ての通り、コストが最小値に収束していません。
学習率が大きすぎると重みの更新が大胆になりすぎて、コストが最小になる重みを超えてしまい、更新を繰り返す度に重みが暴れるように変化してどんどんコストも大きくなってしまいます。
最適な重みから離れていく図
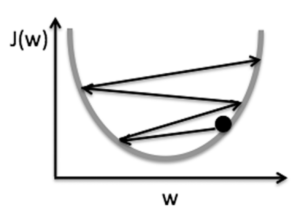
逆に学習率が小さすぎると、コストは小さくなっていっているのですが、収束するまでに日が暮れてしまいます。まあそれは言いすぎですが、効率がよくありません。
スケーリング
では0.0001よりも大きくて0.01よりも小さい学習率でもっかいやってみよう…というのももちろん大事なのですが、勾配降下法をより正確に行うために スケーリング という操作をかまします。
スケーリングにもいくつかありますが、今回は標準化を用います。
標準化は、各特徴量の平均をずらして中心が0になるようにし、各特徴量の標準偏差を1にします。
これによって、もし特徴ごとに特徴量の値が全然違う(例えば花びらの長さとがく片の長さには差がある)ことがあっても平等に扱えるようになることが何となくイメージできるかと思います。
例えばあるデータのj番目の特徴量x_jを標準化するには、訓練データ全体での平均μ_jを全ての訓練データから引いて標準偏差σ_jで割ります。
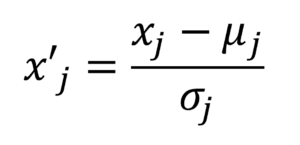
標準化をするコードを以下に記載します。
# データをコピーしてくる
X_std = np.copy(X)
# 各列を標準化
# meanメソッドで平均、stdメソッドで標準偏差を簡単に求められる
X_std[:, 0] = (X[:, 0] - X[:, 0].mean()) / X[:, 0].std()
X_std[:, 1] = (X[:, 1] - X[:, 1].mean()) / X[:, 1].std()
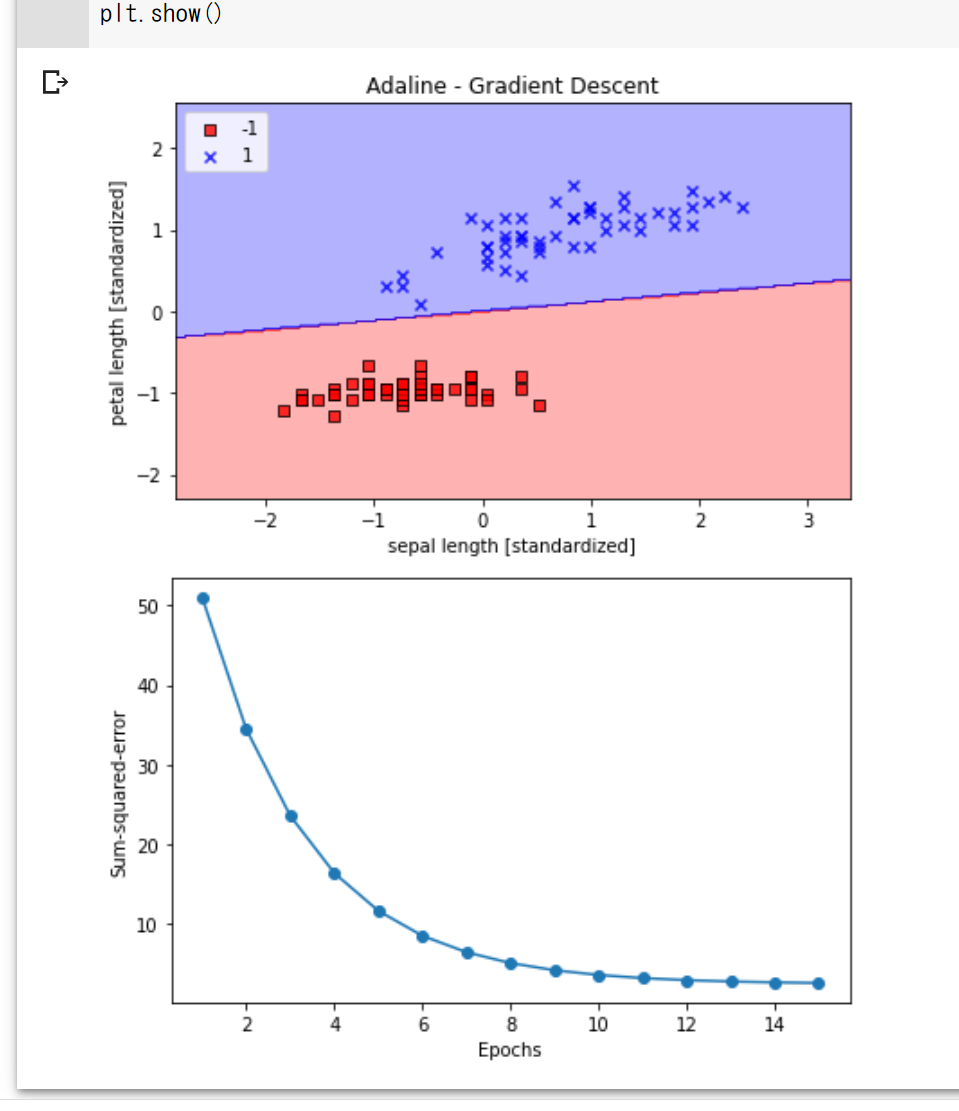
標準化ができたら、今度こそ学習率0.01でADALINEをもう一度訓練させてみます。
# ADALINE分類器をada.gdにセット
ada_gd = AdalineGD(n_iter=15, eta=0.01)
# モデルを適合させて訓練
ada_gd.fit(X_std, y)
# まずデータを分類した図を作成していく
# 境界領域のプロット
plot_decision_regions(X_std, y, classifier=ada_gd)
# タイトルを設定
plt.title('Adaline - Gradient Descent')
# 軸ラベルを設定
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
# 左上に凡例を設定
plt.legend(loc='upper left')
# 図を表示
plt.tight_layout()
plt.show()
# ここからはエポック数とコスト関数の関係を表すグラフを作成していく
plt.plot(range(1, len(ada_gd.cost_) + 1), ada_gd.cost_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Sum-squared-error')
# 図を表示
plt.tight_layout()
plt.show()