STLで季節調整をやってみた話。

目次

1. そもそも季節調整ってなんぞ？
2. 準備
3. とりあえずやってみる
4. 色々な時系列でやってみる
5. まとめ
6. 参考文献

1. そもそも季節調整ってなんぞ？

ある一定の時間間隔で得られたデータの系列（例えば株価や気温の時間変化）のことを、時系列データと呼びます。一部の時系列データ（例えばアイスの売り上げとか）には、１年周期で繰り返す変動（季節変動）が含まれており、時系列データを解釈する際に、この季節変動成分を取り除く作業（＝季節調整）が重要になります。（経済産業省さんのページに丁寧な説明があります。）

今回は局所回帰を用いて季節調整を行うSTL (Seasonal-Trend decomposition procedure based on Loess) (Cleveland et al., 1990) という手法を使って、季節調整をやってみます。ついでに、どんな性質の時系列データになら適用可能か、というのも調べてみました。

個人的なメモなので乱筆ですが、ご容赦ください。

手法の詳細には長くなるので触れません。具体的な手続きが知りたい人は元論文を読んでください。

2. 準備

STLのオリジナルのFORTRAN スクリプトは公開されていますが、私はFortranに馴染みがないので、今回はPythonのstatsmodelsというモジュールを使います。お使いのPython環境にstatsmodelsが入っていない人は、以下のコマンドで追加してください。

conda install statsmodels

初めに、今回使うモジュールをまとめて書いておきます。STLを行う際は、statsmodels内のstatsmodels.tsa.seasonal.STLというクラスを使います。

test_stl.py

import math
import numpy as np
from statsmodels.tsa.seasonal import STL
import matplotlib.pyplot as plt

3. とりあえずやってみる

今回は国土地理院が公開しているGEONET 日々の座標値を模した、日次データを人工的に作成してSTLを適用していきます。

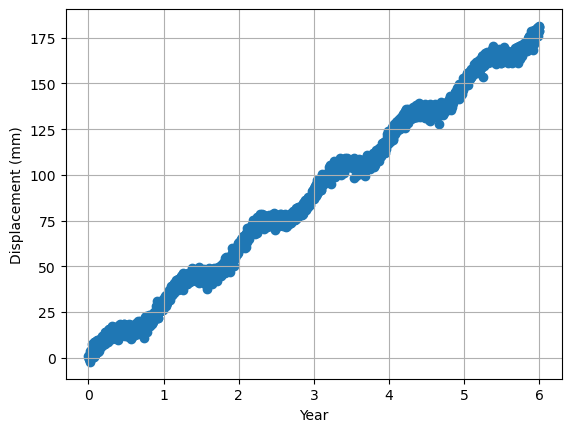
地殻変動観測を目的としたGPSの日座標時系列には、プレート運動などによるトレンド成分と、年周変動成分が含まれています。まずは、トレンド成分を１次関数で、年周変動成分を三角関数で表したデータを作ります。簡単のため、ノイズ成分には標準偏差2 mmの正規分布に従う乱数を使います。データ長は６年分で、閏年は考慮しません。

test_stl.py

# make synthetic dataset
year = 6

t = np.linspace(0,year*365,year*365+1)
trend_syn = 30*t/365
seas_syn = 5*np.sin( 2*np.pi*t/365 )
obs = trend_syn + seas_syn + np.random.normal( 0, 2, len(t) )

plt.scatter(t/365,obs)
plt.xlabel('Year')
plt.ylabel('Displacement (mm)')
plt.grid()
plt.savefig( 'syndata_case1.png', bbox_inches="tight" )

作成した疑似データはこんな感じです。

STLは、与えられた時系列データを、関数形を仮定することなくトレンド成分、季節変動成分、remainder成分に分解します。色々なパラメータを変更することで、推定結果をより良くすることができます。今回は簡単のため、季節変動成分の周期（日次データ＆年周変動なので365）のみ与えて、他のパラメータはデフォルトのものを使います。パラメータの与え方については、公式ページ、もしくは元論文を参照してください。

推定手法の都合上、得られた季節変動成分は時間的に滑らかではありません。今回は適当に、61日の時間窓の移動平均で季節変動を平滑化しています。季節成分の平滑化の方法にも色々あると思うので、手元のデータセットの性質に合わせて選択してください。

test_stl.py

stl = STL( obs, period=365 )
stl_res = stl.fit()
trend_est = stl_res.trend
seas_est0 = stl_res.seasonal
seas_est = np.convolve( seas_est0, np.ones(61)/61, mode="same")

最後に、得られた結果を描画してみます。また、推定結果は二乗平均平方根誤差（プログラム上はRMSと表記しています）を用いて評価しています。

test_stl.py

def plot_stl_result( t, obs, trend_obs, seas_obs, trend_est, seas_est, figname ) :

    # calculate rms
    n = len(t)
    rms_all = np.sqrt( np.sum( ( obs - trend_est - seas_est )**2 )/n )
    rms_trend = np.sqrt( np.sum( ( trend_obs - trend_est )**2 )/n )
    rms_seas = np.sqrt( np.sum( ( seas_obs - seas_est )**2 )/n )
    
    # prepare plotting
    fig = plt.figure(figsize=(12,8))
    xlim = [ np.amin(t)/365-0.5, np.amax(t)/365+0.5 ]
    xticks = np.arange( np.amin(t)/365, 1+np.amax(t)/365, 1 )
    t = t/365
    
    # check data fitting
    ax1 = fig.add_subplot(311)
    ax1.tick_params( which='major', length=7 )
    
    ax1.scatter( t, obs, c='black', label='syn', zorder=1 )
    ax1.plot( t, trend_est + seas_est, linewidth=2, color='red', label='est\nRMS = {0:.2f} mm'.format(rms_all), zorder=2 )
    #ax1.text( 0.8, 0.2, 'RMS = '.format(rms_all), fontsize=15, transform=ax1.transAxes )
    
    ax1.legend(loc='upper left')
    ax1.grid()
    ax1.set_xlim(xlim)
    ax1.set_xticks(xticks)
    ax1.set_xticklabels('')
    ax1.set_ylabel('Displacement (mm)')
    
    # compare trend component
    ax2 = fig.add_subplot(312)
    ax2.tick_params( which='major', length=7, top=True )
    ax2.plot( t, trend_obs, color='black', linewidth=2, label='syn', zorder=1)
    ax2.plot( t, trend_est, color='red', linewidth=2, label='est\nRMS = {0:.2f} mm'.format(rms_trend), zorder=2)
    
    ax2.legend(loc='upper left')
    ax2.grid()
    ax2.set_xlim(xlim)
    ax2.set_xticks(xticks)
    ax2.set_xticklabels('')
    ax2.set_ylabel('Displacement (mm)')
    
    # compare seasonal component
    ax3 = fig.add_subplot(313)
    ax3.tick_params( which='major', length=7, top=True )
    ax3.plot( t, seas_obs, color='black', linewidth=2, label='syn', zorder=1)
    ax3.plot( t, seas_est, color='red', linewidth=2, label='est\nRMS = {0:.2f} mm'.format(rms_seas), zorder=2)
    
    ax3.legend(loc='upper left')
    ax3.grid()
    ax3.set_xlim(xlim)
    ax3.set_xticks(xticks)
    ax3.set_ylabel('Displacement (mm)')
    
    fig.subplots_adjust(hspace=0.1)
    fig.align_ylabels()
    fig.savefig( figname, bbox_inches="tight" )

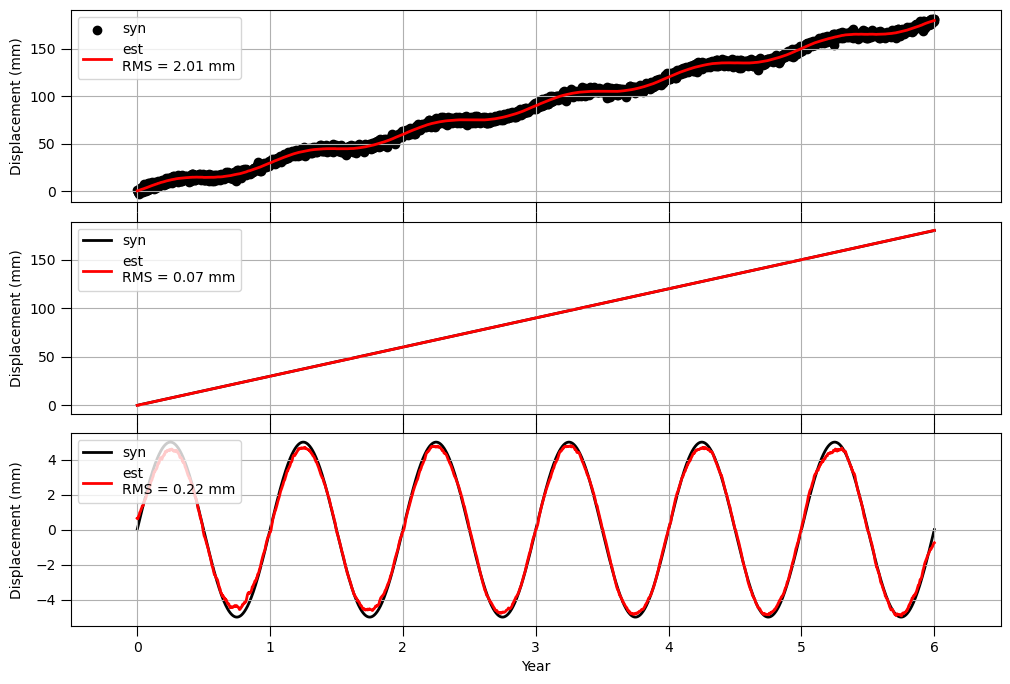
plot_stl_result( t, obs, trend_syn, seas_syn, trend_est, seas_est, 'stlreslts_case1.png' )

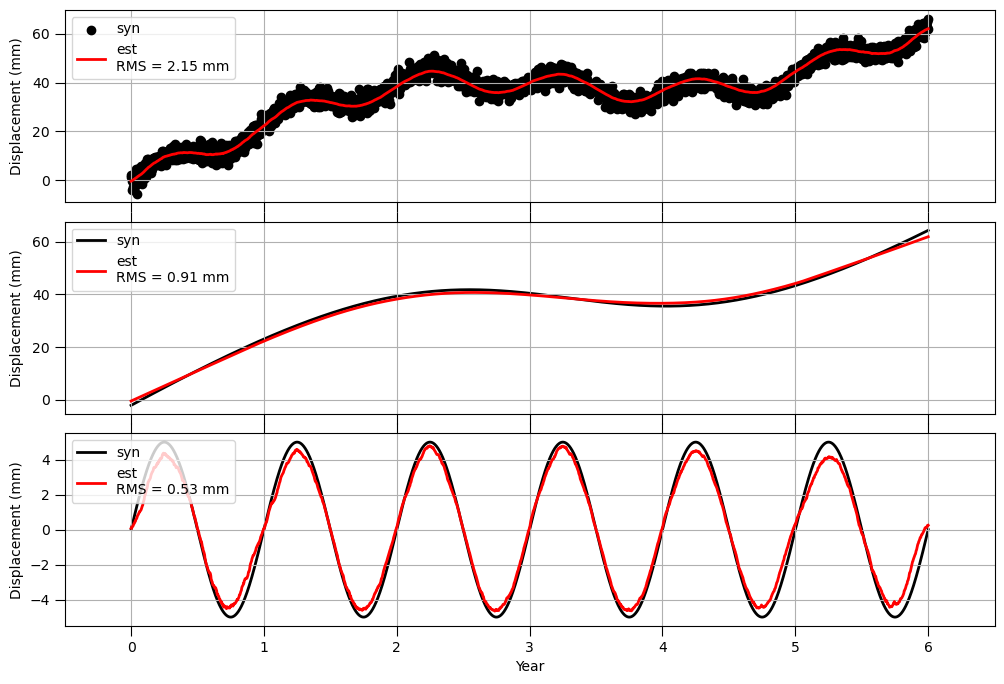
上段は与えたデータと推定値の比較、中段は仮定したトレンド成分と推定値の比較、下段が仮定した季節変動成分と推定値の比較になります。黒線と赤線を比較すると、トレンド・季節変動ともに上手く推定できていることが分かります。

4. 色々な時系列でやってみる

最初の例は、ぶっちゃけ最小二乗法でも同じような季節調整を行うことができる、とても簡単な問題です。しかしSTLの真骨頂は、関数形を仮定することなく、トレンド成分と季節変動成分を柔軟に推定できることにあります。そこでここからは、複雑な季節変動成分とトレンド成分を与えて、季節調整を行っていきます。

季節変動の振幅が時間変化する場合

まずは、季節変動成分の振幅が、時間とともに大きくなる例を考えます。

# make synthetic dataset
year = 6

t = np.linspace(0,year*365,year*365+1)
trend_syn = 30*t/365
seas_syn = (10 + 2*t/365 )*np.sin( 2*np.pi*t/365 )
obs = trend_syn + seas_syn + np.random.normal( 0, 2, len(t) )

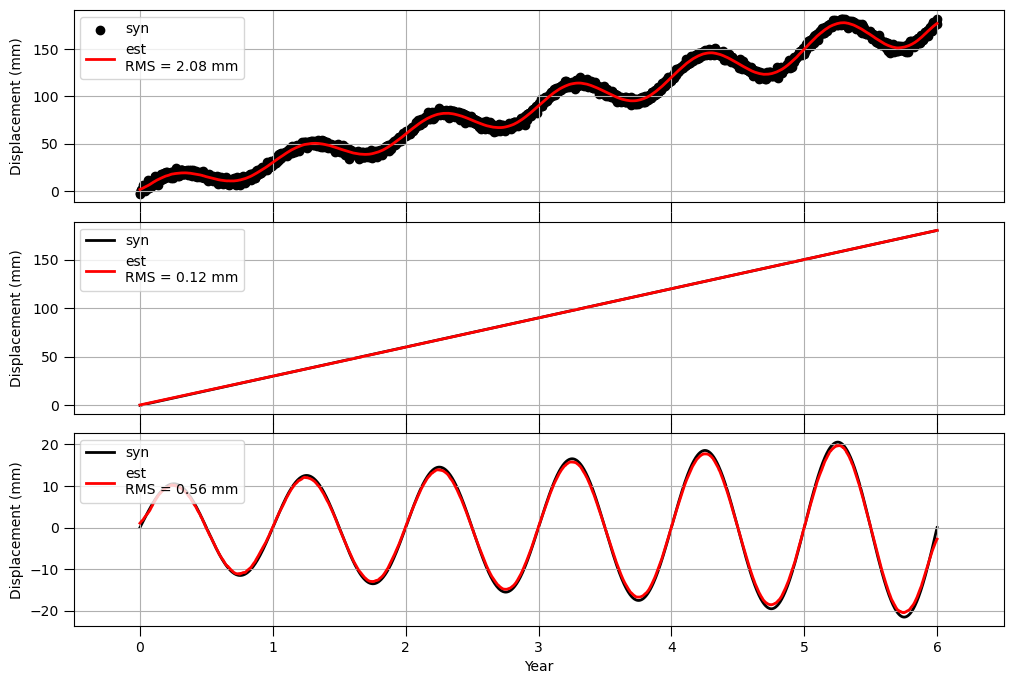
STLの際に与えたパラメータは共通なので、結果の絵のみ掲載します。

綺麗に季節変動を推定できていますね、素晴らしい。

季節変動成分がガウス関数に従う場合

ここまでは季節変動成分を三角関数で与えてきましたが、今回はガウス関数で与えます。

# make synthetic dataset
year = 6

t = np.linspace(0,year*365,year*365+1)
trend_syn = 30*t/365
seas_syn = np.zeros(len(t))

for i in np.arange(year) :

    # set average & standard deviation
    myu = 45 + i*365
    sigma = 30
    seas_syn += -20*np.exp( ( t - myu )**2/( -2*sigma**2 ) )
    
obs = trend_syn + seas_syn + np.random.normal( 0, 2, len(t) )

仮定した季節変動（下段黒線）と推定結果（下段赤線）を比較すると、若干系統的にずれてはいますが、パターンは上手く再現できています。

トレンド成分が滑らかに変化する場合

year = 6

t = np.linspace(0,year*365,year*365+1)
trend_syn = 30*t/365 - 120/( 1 + np.exp(-1*(t - 1200)/300 ) )
seas_syn = 5*np.sin( 2*np.pi*t/365 )
obs = trend_syn + seas_syn + np.random.normal( 0, 2, len(t) )

トレンド成分が滑らかに変化する場合でも、これまでの例と同じく、季節変動を上手く推定できています。

トレンド成分にステップが含まれる場合

year = 6モジュール
amp = 1000

t = np.linspace(0,year*365,year*365+1)
trend_syn = 30*t/365 - amp*np.where( t >= 1000, 1, 0 )
seas_syn = 5*np.sin( 2*np.pi*t/365 )
obs = trend_syn + seas_syn + np.random.normal( 0, 2, len(t) )

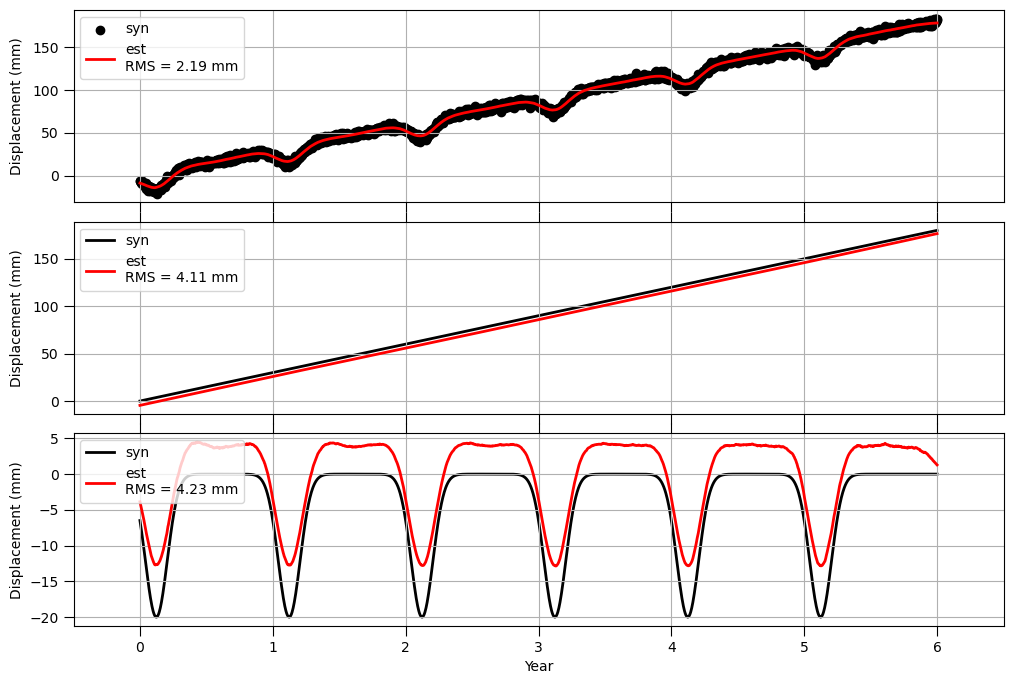
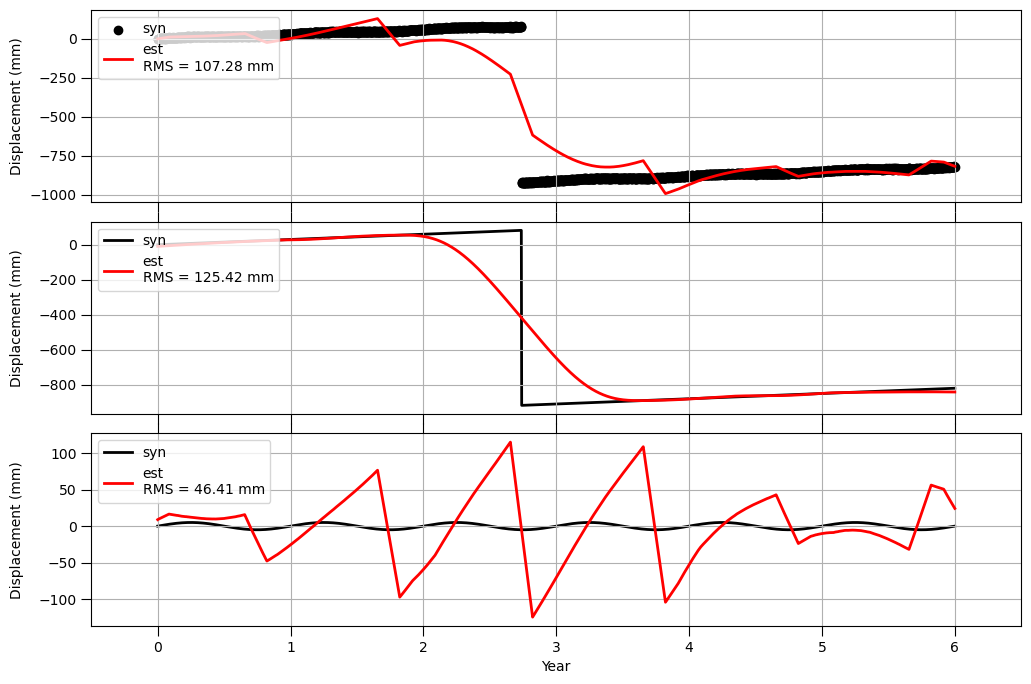
推定値は仮定した時系列をろくに説明できていません。中段のトレンド成分の推定結果をみると、ステップとの処理が離れている期間（2年目以前と4年目以降）については、仮定した時系列を上手く説明できていますが、ステップを仮定した日の前後で大きな乖離が見られます。同様に、季節変動成分の推定結果（下段）も全体的にぐちゃぐちゃになっています。

トレンド成分が急激に変化する場合

year = 6
amp = 50

t = np.linspace(0,year*365,year*365+1)
trend_syn = 30*t/365 + amp*np.where( t >= 1000, 1, 0 )*np.nan_to_num(np.log( 1 + (t - 1000 )/20 )) 
seas_syn = 5*np.sin( 2*np.pi*t/365 )
obs = trend_syn + seas_syn + np.random.normal( 0, 2, len(t) )

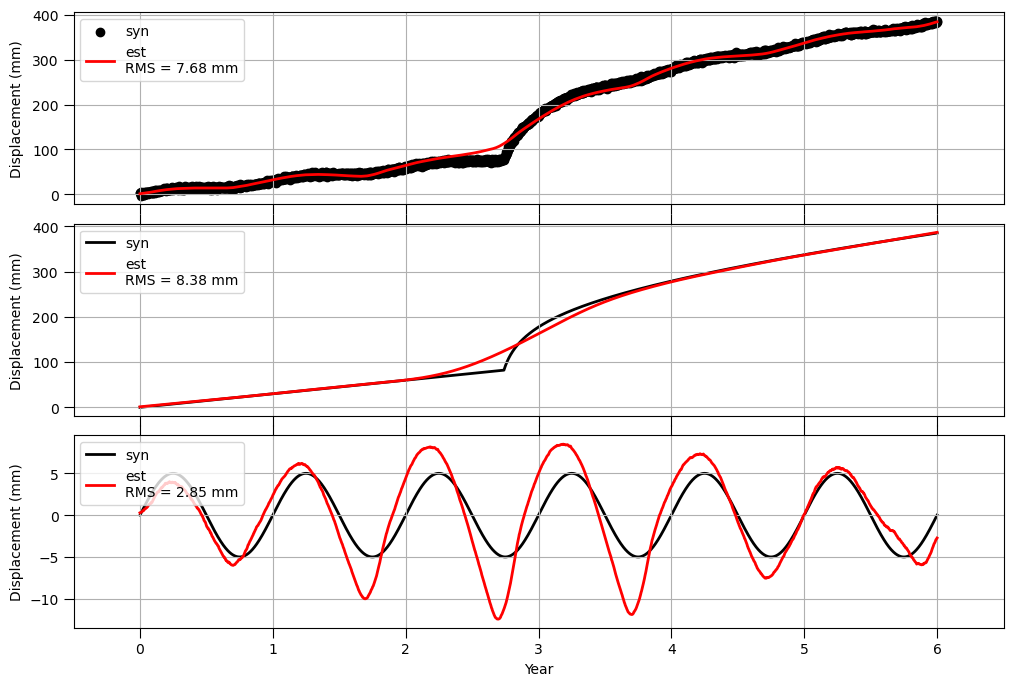
先ほどのケースと比べるとマシですが、トレンド成分の推定値と仮定した時系列の乖離＆季節変動成分の推定精度の悪化が見られます。

5. まとめ

本投稿では、Pythonのモジュールstatsmodelsを使って、STLという季節調整の手法を試してみました。その結果、次の３つのことが分かりました。

• 季節調整を行うこと自体は比較的簡単。
• 滑らかなトレンド変化＆複雑な季節変動成分が含まれている時系列には、STLは絶大な威力を発揮する。
• 時系列データに急激なトレンド変化が含まれている場合、推定結果に悪影響を与える。

6. 参考文献

• 経済産業省 季節調整とは何か？；経済統計の周期性を考える
• Cleveland, R. B., Cleveland, W. S., McRae, J. E., & Terpenning, I. (1990). STL: A seasonal-trend decomposition procedure based on loess. Journal of Official Statistics, 6(1), 3–73. (全文PDFはこちら)
• statsmodels 公式
• statsmodels 公式ページ内のSTLの使い方説明（こちらとこちら）