ナイーブベイズモデル

文書分類やスパムメールフィルタについてよく使われている、ナイーブベイズ(Naive Bays)モデルについてまとめる。
集中講義でナイーブベイズモデルについて考える機会があったので、以下の本を参考にしてナイーブベイズを勉強した。
何か、間違っている点がございましたら、何卒ご指摘ください。

###条件付き独立

ナイーブベイズモデルは最大事後確率識別規則
$$
識別クラス = \mathop{\rm arg\,max}\limits_{k} \ P\left(C = k | \boldsymbol{x} \right)
$$
に従って識別するモデルである。ここでベイズの定理より、
$$
P(C = k | \boldsymbol{x}) \propto P(\boldsymbol{x} | C = k) P(C = k)
$$
なので、識別規則を以下のように書き直せる。
$$
識別クラス = \mathop{\rm arg\,max}\limits_{k} \ P(\boldsymbol{x} | C = k) P(C = k)
$$
$P(C = k)$は事前確率で$P(C=k) = \frac{N_k}{N}$ で計算できる。ここで$N_k$はクラス$C_k$に属するデータの個数である。しかし、尤度$P(\boldsymbol{x} | C = k)$が問題になってくる。単純に推定できないからである。はじパタのベイズの識別規則((詳しくはP21~を参照))では尤度をガウス分布でモデル化し、そのパラメータを最尤推定で求めてやった。ここで、ナイーブベイズは$\boldsymbol{x} = (x_1, x_2, \dots, x_D)$の$D$次元ベクトルの時、それぞれの特徴はクラス$C_k$が与えられたときに独立と仮定する．すなわち条件付き独立である．
条件独立の性質より以下のことが成り立つ。
$$
P(\boldsymbol{x}| C=k) = \prod_{ d = 1 }^D P(x_d | C=k)
$$

よって、識別規則は以下の通りになる。
$$
識別クラス = \mathop{\rm arg\,max}\limits_{k} \ \left(\prod_{ d = 1 }^D P(x_d | C = k) \right) P(C = k)
$$
あとは、特徴一つ一つについて$P(x_d | C = k)$をモデル化してやって、そのモデルのパラメータを最尤推定によって求めてやれば良い。
###最尤推定

ガウス分布

ここでは、$P(x_d | C = k)$をガウス分布によってモデル化した時の最尤推定を求める。つまり、対数尤度$\mathcal{L}$は学習データ数を$N$とすると
$$
\begin{eqnarray}
P(x_d | C = k) = \frac{1}{\sqrt{2\pi \sigma_d^2}} \exp{\left\{ - \frac{(x-\mu_d)^2}{2\sigma_d^2}\right\} }
\end{eqnarray}
$$

$$
\begin{align}
\mathcal{L}(\mu_d, \sigma_d^2)&= \log\prod_{ n = 1 }^N P(x_{nd} | C = k)\
&=\sum_{ n = 1 }^N \log\frac{1}{\sqrt{2\pi \sigma_d^2}} \exp{\left\{ -
\frac{(x_{nd}-\mu_d)^2}{2\sigma_d^2}\right\} } \
&= -\frac{N}{2} \log{(2 \pi)} - \frac{N}{2} \log{\sigma_d^2} - \frac{1}{2\sigma_d^2} \sum_{n=1}^N (x_{nd}-\mu_d)^2
\end{align}
$$

そうすると、以下が得られる。

$$
\begin{align}
\mu_{d} &= \frac{1}{N}\sum_{n=1}^N x_{nd} \tag{1}　\
\sigma_{d} &= \frac{1}{N} \sum_{n=1}^{N} x_{nd} \tag{2}
\end{align}
$$

式$(1), (2)$は直感として得られるものになっている。ここで、はじパタではナイーブ（条件付き独立）は取らず、$P(C=k| \boldsymbol{x})$ を多次元正規分布でモデル化する手法をとっている。つまり、共分散行列

$$
\begin{align}
\varSigma = \frac{1}{N} \sum_{n=1}^N (\boldsymbol{x}_n - \boldsymbol{\mu})(\boldsymbol{x}_n - \boldsymbol{\mu})^T
\end{align}
$$

の対角成分が$0$と仮定していない。特徴同士に相関がある（条件付き独立ではない）としている。scikit-learnのGaussianNBを使うときには，データが無相関ということを仮定していることを意識しなければならない。

以下、尤度$P(\boldsymbol{x} | C = k)$を多次元正規分布でモデル化したときに特徴間に相関がないとすると、ナイーブベイズと同じことをしているということを証明する。

$$
\begin{align}
P(\boldsymbol{x} | C = k \ ; \boldsymbol{\mu}, \varSigma) = \frac{1}{(2\pi)^{\frac{D}{2}}\left|\varSigma\right|^{\frac{1}{2}}} \exp{\left(-\frac{1}{2}(\boldsymbol{x}- \boldsymbol{\mu})^T \varSigma^{-1} (\boldsymbol{x}- \boldsymbol{\mu})\right)}
\end{align}
$$


ここで簡単のため$D = 2$ のときを考えると
$$
\varSigma =
\begin{pmatrix} \sigma_1 & 0 \\ 0 & \sigma_2 \end{pmatrix}
$$
となり

$$
\begin{align}
|\varSigma| = \sigma_1^2 \sigma_2^2
\end{align}
$$

$$
\begin{align}
\varSigma^{-1} = \begin{pmatrix} \frac{1}{\sigma_1^2} & 0 \\ 0 & \frac{1}{\sigma_2^2} \end{pmatrix}
\end{align}
$$
である。また、
$$
\boldsymbol{x} - \boldsymbol{\mu} = (x_1 - \mu_1, x_2 - \mu_2)^T
$$
なので, ガウス分布の指数部は以下の通りになる。
$$
\begin{align}
-\frac{1}{2}(\boldsymbol{x}- \boldsymbol{\mu})^T \varSigma^{-1} (\boldsymbol{x}- \boldsymbol{\mu}) = \frac{1}{2} \left\{ \frac{(x_1 - \mu_1)^2}{\sigma_1^2} + \frac{(x_1 - \mu_2)^2}{\sigma_2^2} \right\}
\end{align}
$$
このとき、
$$
\begin{align}
P(\boldsymbol{x} | C = k\ ; \mu, \varSigma) &= \frac{1}{(2\pi)^{\frac{D}{2}}\sqrt{\sigma_1^2 \sigma_2^2}} \exp{\left\{ - \frac{(x_1 - \mu_1)^2}{\sigma_1^2} - \frac{(x_1 - \mu_2)^2}{\sigma_2^2} \right\}} \notag
\\ &= \left( \frac{1}{\sqrt{2\pi \sigma_d^2}} \exp{\left\{ -
\frac{(x_{nd}-\mu_d)^2}{2\sigma_d^2}\right\} } \right) \times \left(\frac{1}{\sqrt{2\pi \sigma_d^2}} \exp{\left\{ -
\frac{(x_{nd}-\mu_d)^2}{2\sigma_d^2}\right\} }\right) \notag
\end{align}
$$

よって、
$$
\begin{align}
P(\boldsymbol{x} | C = k\ ; \boldsymbol{\mu}, \varSigma) = P(x_1 | C = k\ ; \mu_1, \sigma_1^2) \times P(x_2 | C = k\ ; \mu_2, \sigma_2^2)
\end{align}
$$
となり、確かに相関を無視するとナイーブベイズを行なっていることに相当することがわかる。
####多変数ベルヌーイモデル
尤度をモデル化するときにおいてガウス分布だけでなく多変数ベルヌーイに尤度が従うとモデル化するものもあるらしい。しかし、これは自然言語処理の分野において使われるみたいなので今回は省略。またいずれ、やろうと思う。

####多項モデル

多変数ベルヌーイモデルと同様。

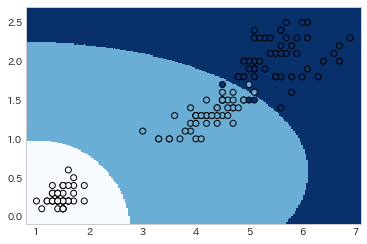
実行例

import numpy as np
import matplotlib.pyplot as plt

# %%
def plotBoundary(clf, X, Y, boundary=True, contour=False):
    """
    識別器の境界をかく
    """
    x_min = X[:, 0].min()
    x_max = X[:, 0].max()
    y_min = X[:, 1].min()
    y_max = X[:, 1].max()

    XX, YY = np.mgrid[x_min: x_max: 200j, y_min: y_max: 200j]
    Z = clf.predict(np.c_[XX.ravel(), YY.ravel()])
    Z = Z.reshape(XX.shape)

    plt.scatter(X[:,0], X[:, 1], c=Y, cmap='Blues', edgecolor='k')
    if boundary:
        plt.pcolormesh(XX, YY, Z, cmap='Blues', zorder=-10)
    if contour:
        Z = clf.predict_proba(np.c_[XX.ravel(), YY.ravel()])[:,1]
        Z = Z.reshape(XX.shape)
        plt.contour(XX, YY, Z)
    plt.xlim(x_min, x_max)
    plt.ylim(y_min, y_max)

if __name__ == '__main__':

    from sklearn.naive_bayes import GaussianNB
    from sklearn.datasets import load_iris
    import pandas as pd

    iris = load_iris()

    X = pd.DataFrame(iris.data, columns=iris.feature_names)
    y = pd.Series(iris.target, name='class')
    Data = pd.concat([X, y], axis=1)
    dic = {i: c for i, c in enumerate(iris.target_names)}
    Data.iloc[:, 4] = Data.iloc[:, 4].map(dic)

    clf = GaussianNB()
    clf.fit(X.iloc[:, 2:4].values, y)
    plotBoundary(clf, X.iloc[:, 2:4].values, y)
    print('score: {:.2%}'.format(clf.score(X.iloc[:, 2:4].values, y)))

結果
score = 96.00%

def plotBoundary(clf, X, Y, boundary=True, contour=False):
    """
    識別器の境界をかく
    """
    x_min = X[:, 0].min()-0.2
    x_max = X[:, 0].max() + 0.2
    y_min = X[:, 1].min() - 0.2
    y_max = X[:, 1].max() + 0.2

    XX, YY = np.mgrid[x_min: x_max: 200j, y_min: y_max: 200j]
        
    Z = clf.predict_proba(np.c_[XX.ravel(), YY.ravel()])[:,1]
    Z = Z.reshape(XX.shape)
    
    plt.scatter(X[:,0], X[:, 1], c=Y, cmap='Blues', edgecolor='k')
    if boundary:
        plt.pcolormesh(XX, YY, Z, cmap='Blues', zorder=-10)
        plt.colorbar()
    if contour:
        plt.contour(XX, YY, Z, cmap='Reds')
        plt.colorbar()
    plt.xlim(x_min, x_max)
    plt.ylim(y_min, y_max)

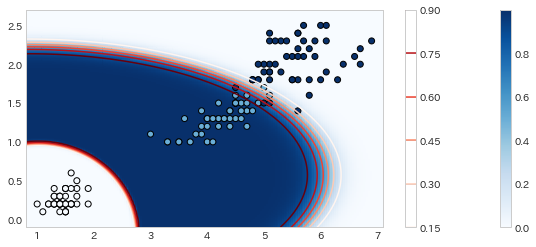
としたときの結果