以下の本を参考にラグランジュ未定乗数法の式の意味を再確認したのでまとめる。
以下のサイトも参考にした。
ラグランジュの未定乗数法の解説と直感的な証明
##ラグランジュの未定乗数法
等式制約条件$g(x, y) = 0$のもと、ある関数$f(x, y)$を最大化または最小化にする際に用いるのがラグランジュの未定乗数法(Lagrange Multipliers)である。
ここで以下の問題を考える。
$$
a
$$
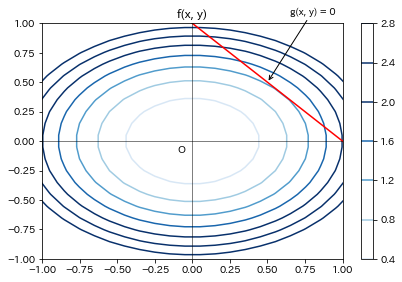
図で表すと以下のようになる。
$x_1 = x, x_2 = y$と書き直すと
これを満たす最適解は
$$
F (x_1,x_2) = f(x_1, x_2) - \lambda g(x_1, x_2)
$$
とおくと、次の式を満たす。
$$
\frac{\partial F}{\partial x_d}=0 \ (d= 0, 1), \ \quad \frac{\partial F}{\partial \lambda} = 0
$$
$\lambda$はラグランジュ乗数と呼ぶ。
$\frac{\partial F}{\partial x_d}=0 \ (d= 0, 1)$ はつまり$\nabla f = \lambda \nabla g$ を意味している。この式は、等高線$f(x, y)$と曲線$g(x, y)=0$の法線ベクトルは平行ということを示している。何故これを満たさなければならないかというと、曲線上で関数$f(x, y)$が極値（最大、最小）を取る点では、その点を通る$f(x, y)$の等高線が曲線に接しているからであり、このことは等高線$f(x, y)$と曲線$g(x, y)=0$の法線ベクトルは平行ということである。
また、
$$
\frac{\partial F}{\partial \lambda} = 0 \
g(x, y) = 0
$$
となり、$\frac{\partial F}{\partial \lambda} = 0$は制約条件そのものを示している。
ラグランジュの未定乗数は、多次元で等式制約が複数個ある時も成り立つ。((詳しくは、これならわかる最適化数学 P76~ 参照))