はじめに
OpenCVを利用して二値化を行う際, 「とりあえずcv2.THRESH_OTSUやっとけばええやろ, ぽいー」って感じでテキトーに二値化してました.
「とりあえずいい感じに動く」って認識だったので, きちんと(?)理解自分なりにここにまとめていきたいと思います.
初心者なので間違いなどあれば教えていただけるとありがたいです.
概要 - OpenCVさんの説明
OpenCVのチュートリアルを見ると
大津のアルゴリズムは以下の式によって定義される重み付けされたクラス内分散を最小にするようなしきい値(t)を探します.
$\sigma_{\omega}^2(t) = q_1(t)\sigma_1^2(t) + q_2(t)\sigma_2^2(t)$
(各変数の定義は本家を見てください)
のように書いてありました.
詳しくはわからなかったけど, いい感じのしきい値(t)を探してくるってことだけわかりました.
概要 - 自分なりの説明
簡単に言うと
ある閾値$t$を境にクラス0とクラス1に分けたとき,
- クラス0とクラス1が離れている
- それぞれのクラス内のデータ群がまとまっている
ような$t$を見つけ出すようになっている.
という感じかなと思いました.
言葉だと少しわかりづらいので, このことをグラフを使って説明していきます.
閾値tを境にクラス0とクラス1に分ける
二値化を適用するのは輝度だけを残したグレースケール画像です.
そのため各画素は$0\sim 255$の値を取ることになります.
ここである閾値$t$を考えると, 下のヒストグラムのように各画素が2つに分断されます.
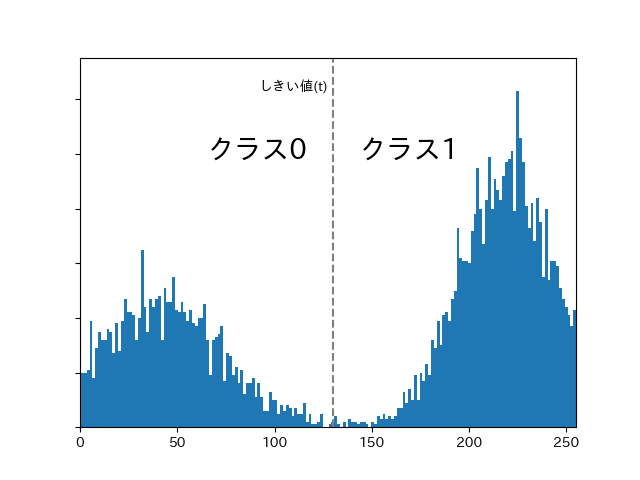
ここで仮に閾値より低い輝度の画素たちをクラス0, 閾値以上の輝度を持つ画素たちをクラス1と呼びます.
クラス0とクラス1が離れている
クラス0の平均とクラス1の平均を出し, それらをうまいぐらいに利用してクラス0とクラス1がどのくらい離れているかを求めます.
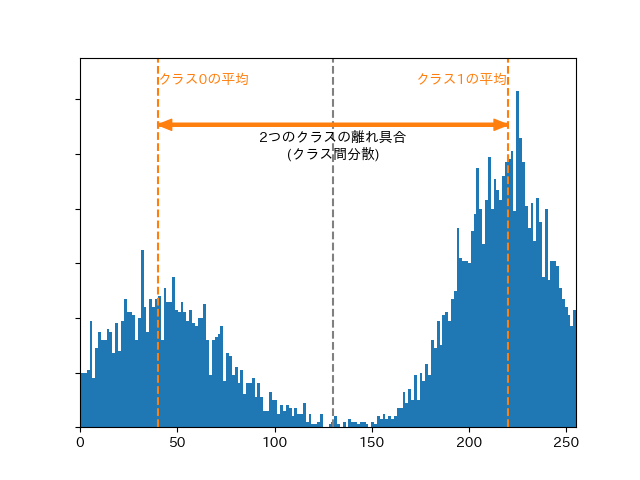
(わかりづらいですが, 離れ具合は「二つのクラスの平均の差」ではないです)
ある閾値$t$で二値化することを考えると, 分断されてできた2つのクラスはなるべく離れていた方がより良さそうです.
それぞれのクラス内のデータ群がまとまっている
各クラスのデータが総合的に見てまとまっているかどうかを, 各クラス内での分散を用いて算出します.
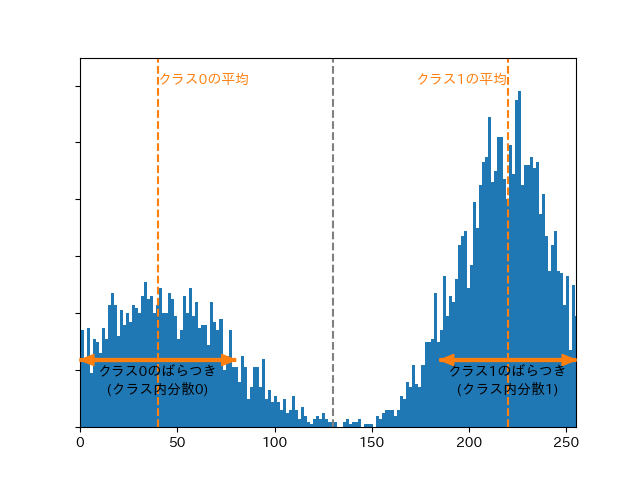
ある閾値$t$において, クラス0のデータ群がまとまって(=分散が小さい)おり, クラス1もまたデータ群がまとまっていると良さそうな感じがしますね.
詳細 - 大津の二値化アルゴリズムの中身
全体の画素数$P_{all}$, クラス0に含まれる画素数$P_{0}$, クラス1に含まれる画素数$P_{1}$とすると,
全体におけるクラス0の割合$R_0$, 全体におけるクラス1の割合$R_1$は
R_{0}=\frac{P_0}{P_{all}} ~~ , ~~ R_{1}=\frac{P_1}{P_{all}}
になります.
全ての画素の輝度($0\sim 255$)の平均を$M_{all}$, クラス0内の平均を$M_{0}$, クラス1内の平均を$M_{1}$とした時,
クラス0とクラス1の離れ具合である**クラス間分散$S_{b}^2$**は以下のように定義されています.
\begin{array}{ccl}
S_b^2 &=& R_0\times (M_0 - M_{all})^2 ~ + ~ R_1\times (M_1 - M_{all})^2 \\
&=& R_0 \times R_1 \times (M_0 - M_1)^2
\end{array}
またクラス0内の分散を$S_0^2$, クラス1の分散を$S_1^2$とすると,
各クラスごとの分散を総合的に評価した**クラス内分散$S_{in}^2$**は以下のように定義されています.
S_{in}^2 = R_0 \times S_0^2 ~ + ~ R_1 \times S_1^2
ここで先ほどの話を持ってきましょう.
ある閾値$t$があったとき, 以下の条件を満たすとき, より好ましいと言えました.
- クラス0とクラス1がより離れている
- クラス毎にまとまっていたほうがよい
条件1はクラス間分散$S_b^2$が大きければ満たせそうです.
また条件2はクラス内分散$S_{in}^2$が小さければ満たせそうです.
つまりクラス間分散を分子に, クラス内分散を分母に持ってきて,
\frac{S_b^2}{S_{in}^2}
が大きくなればよりよい閾値$t$と言えそうです
この式を**分離度$X$**とします.
分離度$X$を最大化するにはどうすればよいでしょうか.
ここで全体の分散$S_{all}=S_b^2 + S_{in}^2$を考えると,
全体の分散は閾値$t$に依らない値なので, ここでは定数と考えることができます.
なので分離度$X$を変形して,
X=\frac{S_b^2}{S_{in}^2}=\frac{S_b^2}{S^2 - S_b^2}
とすると, 分離度$X$を最大化するには, 全体の分散$S$は定数なので「$S_b^2$を大きくすれば良い」ということが分かります.
つまり最適な閾値$t$は
S_b^2 = R_0 \times R_1 \times (M0 - M1)^2
が最も大きくなるようなものである.
と結論付けられます.
なので大津の二値化では$0\sim 255$のすべてを閾値に選んだ時, 最も$S_b^2$が大きくなる数値を適切な閾値として選択するようになっています.
グラフはこちら
要らないと思いますけど, グラフを作ったソースコードを置いておきます.
https://github.com/haru1843/qiita_thresh_otsu