GANがデータの生成分布を獲得していくのをGaussian Mixture 分布を用いたToy Problemに適用することで可視化しました.
実装時の条件は以下の通りです.
Python: 3.6.4
Chainer: 4.1.0
Matplotlib: 2.2.2
Seaborn: 0.8.1
Numpy: 1.14.3
前置き
最近,色々と騒がれているGANですが,
Progressive Growing of GANs for Improved Quality, Stability, and Variation

を昨年末に見て,こりゃスゲーなーと思い,研究テーマにGANを選びました.この解像度レベルでStackGANをやってみたいなぁと思っています.
GANの基本構造については以下が,Kerasのサンプルコードもついており,大変参考になります.バージョンが少し古いですが...
僕はまず,GANの基本的な論文を読み,
論文の再現,真似ごとから初めたのですが,Mode Collapseと呼ばれる現象に悩まされました.
これはGeneratorがほぼ同一のデータしか出力しなくなる現象のことです.

この画像は,自分で Labeled Faces in the Wild のデータを用いて学習させ,300epoch後の同一コード($\boldsymbol{z}$のこと)での生成画像です.1行目2,3列, 5行目3,4列の顔がほぼ同じのように見えます.ひどい時は全生成画像が同じ顔になってしまいます.
これを少し小難しく?説明するとここより,
In the real world, distributions are complicated and multimodal, for example, the probability distribution which describes data may have multiple “peaks” where different sub-groups of samples are concentrated. In such a case a generator can learn to yield images only from one of the sub-groups, causing mode collapse. This happened in my research and I was getting the same output for different input noises.
だそうです笑
GANは実際にどのようにしてデータの生成分布を近似していくのかが複雑でとっつきにくいです.なのでこの学習過程を可視化したいなぁと思いました.
そこでUnrolled Generative Adversarial Networksの Figure 2 を真似ることに決めました.

これは簡単なToy ProblemでGANの学習を可視化した図です.
今回僕が使った実装はここにあります.Toy Problem となるデータの生成法は
を勝手に真似ました.ありがとうございます.
Toy Problemのデータ概要
GANには学習データとして,見本となるデータ(生成したデータ)が必要でした.Mode Collapseが起きやすいように,8つのピークを持つ Gaussian Mixture 分布をGANが近似したいデータの生成分布とし,そこからサンプリングされたデータを学習データとしました.
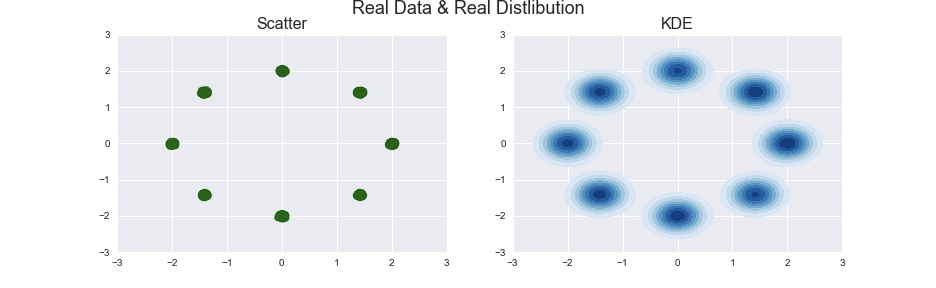
右は,実際に使った学習データ10000個,左はデータからカーネル密度推定により近似したデータの生成分布です.
カーネル密度推定は杉山先生のこの資料で概要を勉強したくらいです...
バンド幅の決め方は Seaborn の seaborn.kdeplot() でのデフォルト引数だった scottを使いました.
GANの学習がうまくいけば,Generatorが生成する2次元データのカーネル密度推定は右図のようになるはずです.
実験条件
Model
モデルは以下のように指定しました.少しわかりにくいですが...もっと良い書き方があれば教えて欲しいです.
- Generator
| 層 | パラメータ | 出力時のshape |
|---|---|---|
| 1層目(入力層) $z$ | dim=100 | (N, 100) |
| 2層目 | Linear (out_size=128, activation=ReLU) | (N, 128) |
| 3層目 | Linear (out_size=128, activation=ReLU) | (N, 128) |
| 4層目(出力層) | Linear (out_size=128, activation=None) | (N, 2) |
- Discriminator
| 層 | パラメータ | 出力時のshape |
|---|---|---|
| 1層目(入力層) | (N, 2) | |
| 2層目 | Linear (out_size=128, activation=ReLU) | (N, 128) |
| 3層目(出力層) | Linear (out_size=128, activation=None) | (N, 1) |
その他の実験条件
- データ数: 10000
- データは-1~1の間に正規化した.
- コード $z$ の次元数: 100
- バッチサイズ: 128
- エポック: 200
- seed: 0, 1, 2 の3つ1.
- OptimizerはGenerator, Discriminator共にAdamを使用しました.また,共に以下のようにハイパーパラメータを指定しました.
| パラメータ | 値 |
|---|---|
| alpha | 1e-4 |
| beta1 | 0.5 |
| beta2 | 0.999 |
| epsilon | 1e-8 |
実験結果
実験条件で示したモデルで学習していきます.
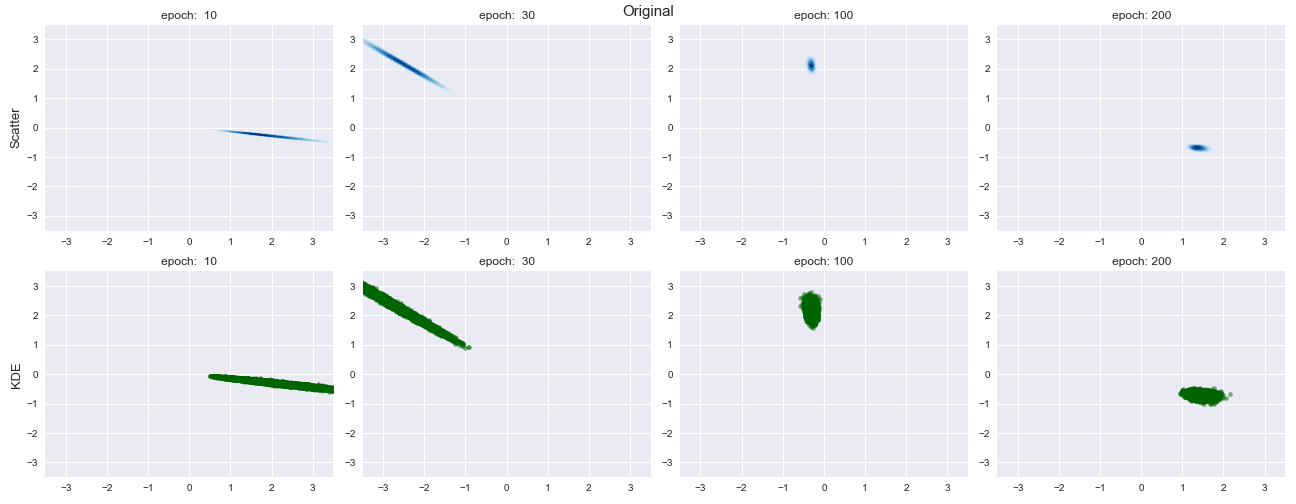
結果は以下のようになりました.
データ分布のある一点のみを近似しており,生成データの多様性がなくなっていることがわかります.
これがいわゆる Mode Collapseです.
Feature Matching
ここで,Improved Techniques for Training GANsよりMode Collapseの対応策として有名な Minibatch Discriminationと Feature Matchingを適用したいと思います.
まず,Feature Matchingを行います.これはかなり簡単で,
Feature Matchingはその時の Discriminatorに関しての Overtrainingを防ぐ新しい目的関数を作ることで,GANの不安定さに対処します.具体的には,GeneratorがDicriminatorの中間層の特徴量の期待値にマッチするように学習させる手法であり,以下のようにGeneratorの目的関数を定義します.
\begin{align}
\min_G \; \left\| \mathbb{E}_{\boldsymbol{x} \sim p_{data}} \boldsymbol{f}(\boldsymbol{x}) - \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})} \boldsymbol{f} (G(\boldsymbol{z})) \right\|_2^2
\end{align}
ただし,$f(\boldsymbol{x})$は Discriminatorの中間層の出力を表します.
実際にはMinibatch上でLossを測るので,プログラムでは以下の関数を最小化するように最適化していきます.
\begin{equation*}
\min_G \; \left\| \frac{1}{N}\sum_n \boldsymbol{f}(\boldsymbol{x_n}) - \frac{1}{N}\sum_n \boldsymbol{f} (G(\boldsymbol{z_n})) \right\|_2^2 \tag{1}
\end{equation*}
Discriminatorはトレーニングによって,本物か生成されたものかを最も判別可能な特徴量を見つけようとするので,この手法は自然な選択であると言えます.オリジナルのGANのLossでは,データ分布と全く同じになる最適解が存在しましたが, Feature matching はGeneratorの損失関数に手を加えてしまうため,この最適解に達するかの保証はないです.しかし,論文ではオリジナルでは不安定だったシチュエーションにおいて実験的に Feature matching は効果的であったと言っています.
- GeneratorのLossを式(1)にするとともに,Discriminatorを以下のように変更しました.表中の注釈に主な変更点を書いています.
| 層 | パラメータ | 出力時のshape |
|---|---|---|
| 1層目(入力層) | (N, 2) | |
| 2層目 | Linear (out_size=128, activation=ReLU)2 | (N, 128) |
| 3層目(出力層) | Linear (out_size=128, activation=None) | (N, 2) |
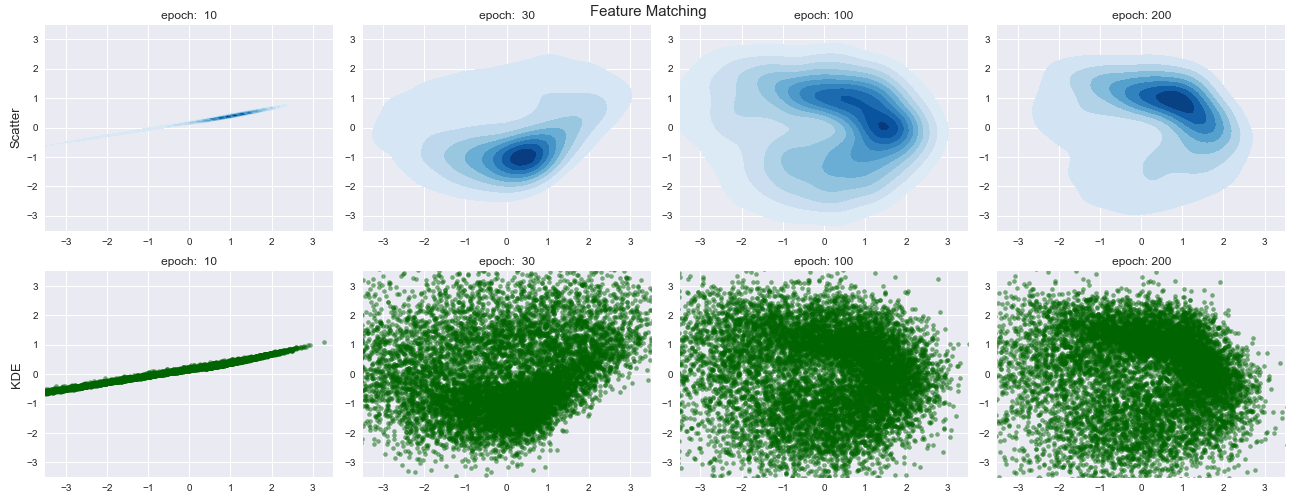
Feature Matchingを Toy Problemに適応した結果が以下の通りです.
確かに生成データが固まらず,広がってくれていますが正確なデータ生成分布に収束することはありませんでした.
ネット上でFeature Matchingを調べると,Feature MatchingのLossを 式(1)にオリジナルのLossを加えた以下のように定義しているものもありました.
\frac{1}{N}\sum_{n=1}^N \log\left( D\left( G(\boldsymbol{z}) \right)\right) + \lambda \times \left\| \frac{1}{N}\sum_n \boldsymbol{f}(\boldsymbol{x_n}) - \frac{1}{N}\sum_n \boldsymbol{f} (G(\boldsymbol{z_n})) \right\|_2^2
この関数を評価関数とし,$\lambda=10$とした結果が以下の通りです.
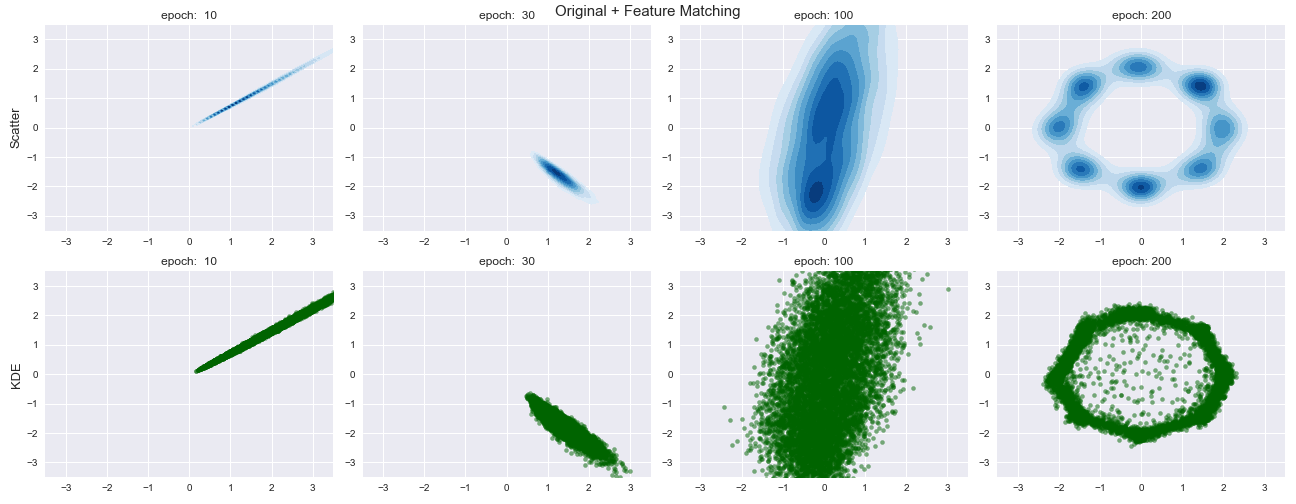
最終的な結果はかなり正確にデータの生成分布を近似できていることがわかります.
最初は$\lambda=1$で試したのですが,Feature MatchingのLossが元々小さいので意味がありませんでした.また,$\lambda=30$とした場合では,$\lambda=10$とあまり変化はありませんでした.
Feature Matchingは簡単なのですが,Feature Matching を適用するときはどの層の出力後に適用すべきなのかがよくわかりません.実装例を見てみると,出力層前のConv Layerに適用するのが一般的?と思いました.なので今回もそのように実装しました.
Minibatch Discrimination
次はMinibatch Discriminationです. Mode CollapseはDiscriinatorが各データを独立に処理し,Generatorの出力が各データと,より異なるようにというメカニズムがないために引きおこされる問題であるということができます.Minibatch DiscriminationはDiscriminatorにミニバッチ内のデータ全体を見て処理する機能を与える手法です.Minibatch Discriminationは,ミニバッチ内のデータの多様性を,ミニバッチのデータ間の距離から測ります.ザクっとした説明は以下の通りです.
ミニバッチを $\boldsymbol{X} \in \mathbb{R}^{N \times D}$ としたとき,ミニバッチの $n$ 番目のサンプル $\boldsymbol{x}_n$ を入れた時の,Discriminatorのある中間層の特徴ベクトルを $\boldsymbol{f}(\boldsymbol{x_n}) \in \mathbb{R}^{A}$ とします.
そして, $\boldsymbol{f}(\boldsymbol{x_n})$ にテンソル $T \in \mathbb{R}^{A \times B \times C}$をかけ, $M_n \in \mathbb{R}^{B \times C}$ を得ます3. $M_n$ をc次元行ベクトルがB個並んだものと考え,行ごとに $n \in [N]$ との $L_1$-distance をとります.さらに,負の指数をとり,以下を得ます.この時,$B, C$はハイパーパラメーターです.
\begin{equation}
c_b(\boldsymbol{x}_i, \boldsymbol{x}_j) = \exp\left(- \| M_{i, b} - M_{j, b} \|_{L_1} \right)
\end{equation}
ここで,$b \in [B], i, j \in [N]$です.minibatch discrimination layerの$\boldsymbol{x}_n$についての出力$o(\boldsymbol{x}_n)$は他のミニバッチ内のデータ全てとの和で定義されます.
\begin{align}
o(\boldsymbol{x}_n)_b &= \sum_{j=1}^N c_b(\boldsymbol{x}_i, \boldsymbol{x}_j) \in \mathbb{R} \\
o(\boldsymbol{x}_n) &= \left[ o(\boldsymbol{x}_n)_1, o(\boldsymbol{x}_n)_2, \dots, o(\boldsymbol{x_n})_B \right] \in \mathbb{R}^{B} \\[6pt]
o(\boldsymbol{X}) &= \begin{pmatrix}
o(\boldsymbol{x}_1) \\[2pt]
o(\boldsymbol{x}_2) \\[2pt]
\vdots \\[2pt]
o(\boldsymbol{x}_N)
\end{pmatrix}\in \mathbb{R}^{N \times B}
\end{align}
最後に,minibatch discrimination layerの出力 $o(\boldsymbol{X})$ と中間層の特徴ベクトル
$\boldsymbol{f}(\boldsymbol{X})$ とを結合し,結果を次の層の入力として与える.この計算をGeneratorからのサンプルのミニバッチ内と学習データからのサンプルのミニバッチ内でそれぞれ別々に行います.従来のように,Discriinatorは各データに対して,そのデータが本物である確率を表す数字を出力するようにします.Discriminatorのタスクは実質的に,そのデータが本物かどうかを識別することです.しかし,今ではサイド情報として,ミニバッチ内の他のサンプルを使うことができます.また, Minibatch Discrimination は視覚的に魅力的なサンプルを素早く生成させることを可能にさせると論文に書いてありました.
Minibatch Discriminationの結果は以下のようになりました.
ハイパーパラメータである$B, C$はそれぞれ$32, 8$としました.
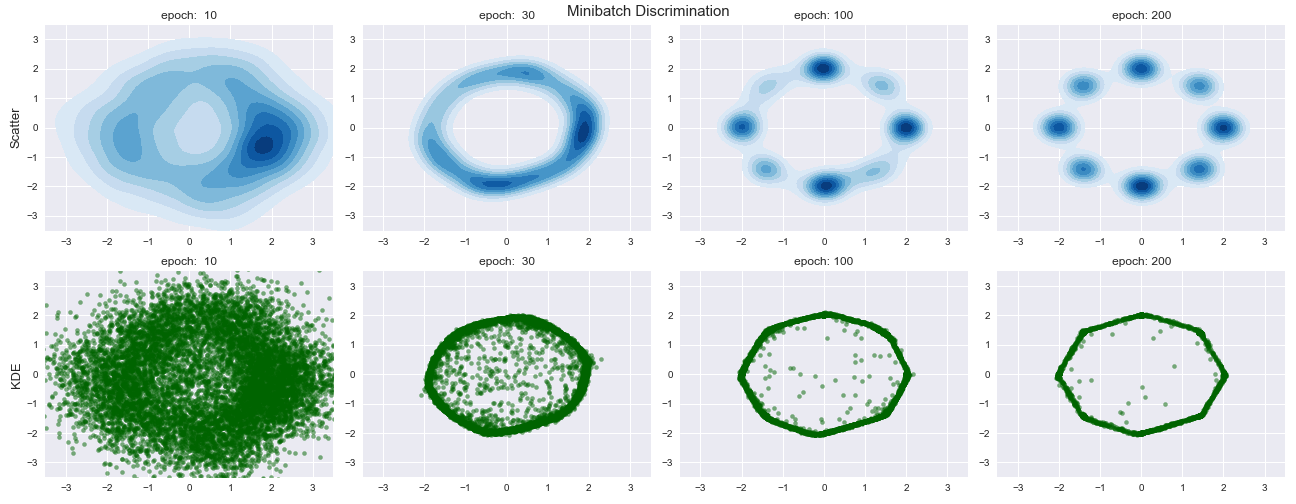
Feature Matchingよりも正確に生成分布を近似することができています.また,かなり早い段階でデータの生成分布を捉えていることが図よりわかります.
しかし,Minibatch Discriminationではハイパーパラメータ$B, C$をどの値に設定すればいいのか,またFeature Matchingと同様にどの層に適用すればいいのか4などの問題があります.
終わりに
今回はMode Collapseとはどんなものなのかを,その対応策とともに可視化しました.
GANは学習過程が複雑なのでこのような単純な問題を考えるとGANが親やすくなりますね 笑
次はWGANについて勉強して,簡単な問題で実験したいと思います.その前にWGANが理解できるのかが気になりますが...
間違い,ご意見などがありましたら,是非ともおっしゃって下さい.
-
実際にはGPUを用いており,正確には再現性がないかも?cuDNNを使用していない気もするが... ↩
-
ここの活性をGeneratorの式(1)のLossに使用.ただし,活性化関数を通す前の値を使用. ↩
-
実際にはテンソルではなく,行列 $T \in \mathbb{R}^{A \times (B \times C)}$をかけ,
reshapeすることで $M_n \in \mathbb{R}^{B \times C}$ を作ります. ↩ -
DiscriminatorがLossを構成するときに,ミニバッチ内の多様度(つまり,Minibatch Discriminatorの出力)を使いたいので,出力層の1つ手前でいいのではないかと思っています.今回の実験でもそうしました. ↩