0.概要
機械学習の分野では変分ベイズもとい変分推論が多く取り扱われるようになってきている。変分推論の「変分」は、変分法からきており、これを理解しないことには変分推論の式展開も容易に行うことはできない。そこで、まずは変分法から入門していきたい。
1. 変分法
変分法について説明する。
微分法
微分法は、一般的に関数$f(x)$の最適化問題を考える際に、その関数を最小化・最大化するような$x$を求める。これは関数$f(x)$を微分し、導関数$\dfrac{df(x)}{dx}$を0にするような値を探すことである。
\dfrac{df(x)}{dx}=0
変分法
変分法は、ある関数$y(x)$によって決定される関数$I$の最適化問題を考える際に、その関数$I$を最小化・最大化するような$y(x)$を求めることである。これは関数$I$、すなわち汎関数の微小変化を0にする関数$y(x)$を探すことである。
\delta I=0
微分法では変数$x$を微小変化させると変数$y$にどれくらいの感度があるのかを見ていたが、変分法では関数の変化量を見るため、関数そのものが対象である。すなわち、微分法は1つのグラフの線状を見るが、変分法では関数そのものの形がどのように変化したのかを見る。
汎関数
関数$I$、すなわち汎関数は関数の関数を指す。例えば、$y=f(x)$という関数の$x=0$から$x=1$までの長さを$L(f)$とおいたとき、この関数の線積分、すなわち曲線の長さは以下で与えられる。
L(f) = \int^{x=1}_{x=0} \sqrt {1+f'\left( x\right) ^{2}}dx
この時、関数$L$は関数$f$によって決定される。すなわち、$L$は関数$y=f(x)=y(x)$の関数といえる。汎関数は関数そのものの変化率を示すため、対象とする関数$y(x)$を積分することによって得られる。
ここで汎関数$I$を以下のように定義する
I(y) \equiv \int^{b}_{a} f(x, y, z) dx \\
\equiv \int^{b}_{a} f(x, y(x), y' (x)) dx
ここで$f$を被積分関数、$x$は入力、$y(x)$は出力、$y'(x)$は$\dfrac{dy}{dx}$で変化量を表す。
また、常に中身を全て書くと面倒なので、以下のように省略されることもある。
I(y) \equiv \int^{b}_{a} f(x, y, z) dx \equiv \int^{b}_{a} f(x, y(x), y'(x)) dx
\equiv f[y(x)]
変分問題(イメージ)
変分問題とは、$\int^{b}_{a} f(x, y(x), y') dx $の$y(x)$を求めることである。単純な問題として以下の最小化問題が与えられたとする。
I(y) = \int^{2}_{1} \{1 + y(x)\}^2 dx
ここで$I(y)$を最も0に近づける関数$y(x)$を考える。これが変分問題である。
例えば、以下のように関数$y(x)$を定義したとする。
y(x) = -1
その場合、全ての$x$において以下のようになり、最小値を取ることとなる。
I(y) = \int^{2}_{1} \{1 - 1\}^2 dx \\
ここで$y(x)=x^3$等を定義した場合、$x=-1$等の限られた場合にしか最小値を取り得ない。
次に$y(1)=-3$及び$y(2)=-6$といった制約が与えられたとき$y(x)$は、
y(x) = -3x
と定義できる。よって、
I(y) = \int^{2}_{1} \{1 - 3x\}^2 dx \\
= \int^{2}_{1} [3x^3 - 3x^2 + x + c]^{2}_{1}
= [14] - [1] = 13
$y(x) = -3x$が制約を満たす最小の関数となる。
汎関数の方向微分(ガトー微分)
微分法でいうところの方向微分を関数で行う。これをガトー微分という。
ある関数をある方向$v$に向けて微小変化$\varepsilon$させたものを以下のように定義する。
y(x+\varepsilon v)
次に、ある関数と、ある関数をある方方向に向けて微小変化させた変化量を以下のように定義する。
I(y+\varepsilon v) - I(y)
平均変化率の求め方は、微分法でいう数値微分に方向を付けるだけである。
よって、
\dfrac{I(y + \varepsilon v) - I(y)}{ \varepsilon}
となる。
公式として、汎関数が以下のように与えられたとき、
I(y) \equiv \int^{b}_{a} f(x, y, z) dx \equiv \int^{b}_{a} f(x, y(x), y'(x)) dx
ガトー微分は
DI(y) \equiv \int^{b}_{a} \{f_y[y(x)]v(x)+f_z[y(x)]v'(x)\} dx
と表せる。ここで、$f_y$は$y(x)$、$f_z$は$y'(x)$に関する偏微分である。
ガトー微分の例
例えば汎関数が以下の場合、
I(y) = \int^{1}_{0} y(x) + \dfrac{1}{2}y'(x)^2 dx
被積分関数は$I(y)=f(x, y, z) = y+\dfrac{1}{2}z^2$で、$f_y = y(x) = 1$で、$f_z = z$なので、
DF(y)(v)=\int^{1}_{0} 1 \cdot v(x) + y'(x)v'(x) dx
となる。
Euler-Lagrange方程式
関数$I$が最適化(最大・最小)されるように関数$f$を求めるのが変分問題である。
I(y) \equiv \int^{b}_{a} f(x, y, z) dx \equiv \int^{b}_{a} f(x, y(x), y'(x)) dx
\equiv f[y(x)]
停留値の付近では関数を微小変化させたときの汎関数の変化$\delta I$が非常に小さいことに着目する。$\delta I$を第一変分という。
$y(x)$の初期状態$y_{0}(x)$を、任意関数$\eta$と微小量$\varepsilon$を用いて変化させる。
y(x) = y_0(x)+\varepsilon \eta(x)
もし$\varepsilon = 0$のとき、変分問題の解$I(y)$が停留値を示すのであれば以下が成り立つ
\dfrac{dI(y)}{d \varepsilon} |_{\varepsilon=0} = 0
汎関数が微小変化しない停留点、すなわち最適化された状態を示している。
因みに$\delta I = 0$のことを臨界点、停留点と呼ぶ。
では、実際に汎関数を微分していく。まず汎関数を埋め込む。
\dfrac{dI(y)}{d \varepsilon} |_{\varepsilon=0} = \dfrac{d}{d \varepsilon} \int^{b}_{a} f(x, y(x), y'(x)) dx |_{\varepsilon=0}
次にこれを展開していき
=\int^{b}_{a} {\dfrac{\partial f}{\partial y (x)} \cdot \dfrac{\partial y (x)}{\partial \varepsilon} + \dfrac{\partial f}{\partial y'(x)} \cdot \dfrac{\partial y'(x)}{\partial \varepsilon} } dx
$y(x) = y_0(x)+\varepsilon \eta(x)$を$\varepsilon$偏微分したら$\eta$が出てくることを用いて整理し、
= \int^{b}_{a} {\dfrac{\partial f}{\partial y (x)} \eta(x) + \dfrac{\partial f}{\partial y'(x)} \eta'(x)} dx
第二項を部分積分すると以下のようになる。
=[\dfrac{\partial f}{\partial y' (x)} \eta(x)]^{b}_{a} + \int^{b}_{a} \eta(x) \left\{ \dfrac{\partial f}{\partial y(x)}-\dfrac{d}{dx}(\dfrac{\partial f}{\partial y'(x)}) \right\} dx
なお、$\eta$は元のグラフの両端では変化がないように制約を与えるため$\eta (a) = \eta (b) = 0$となり、
この境界条件により、前に出した部分積分は0になり、消える。
よって、
\dfrac{dI(y)}{d \varepsilon} |_{\varepsilon=0} = \int^{b}_{a} \eta(x) \left\{ \dfrac{\partial f}{\partial y(x)}-\dfrac{d}{dx}(\dfrac{\partial f}{\partial y'(x)}) \right\} dx
と整理することができる。$\eta$は任意の関数のため、0になるためには右辺を0にする必要がある。
\dfrac{\partial f}{\partial y(x)}-\dfrac{d}{dx}(\dfrac{\partial f}{\partial y'(x)}) = 0
これがEuler-Lagrangeの方程式である。
Euler-Lagrangeの方程式を用いた変分法
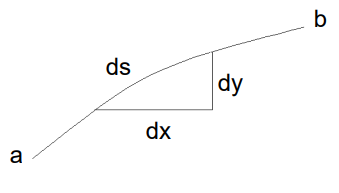
この時、距離$l$は直線の微小量の積算なので以下で与えられる
l(c) = y(x) = \int ds = \sqrt{dx^2 + dy^2}
よって、汎関数は$f(t, c, c') = l$である。
この時、$c$は2次で与えられるためEuler-Lagrangeの方程式は2次元連立微分方程式となる。
\dfrac{\partial f}{\partial x(t)}-\dfrac{d}{dt}(\dfrac{\partial f}{\partial x'(t)}) = 0 \\
\dfrac{\partial f}{\partial y(t)}-\dfrac{d}{dt}(\dfrac{\partial f}{\partial y'(t)}) = 0
次に、E-L方程式の$\dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial x'}, \dfrac{\partial f}{\partial y}, \dfrac{\partial f}{\partial y'}$を求める
\dfrac{\partial f}{\partial x(t)'} = \dfrac{dx(t)}{\sqrt{dx(t)^2 + dy(t)^2}}\\
\dfrac{\partial f}{\partial y(t)'} = \dfrac{dy(t)}{\sqrt{dx(t)^2 + dy(t)^2}}\\
\dfrac{\partial f}{\partial x} = 0 \\
\dfrac{\partial f}{\partial y} = 0
これより、E-L方程式を以下のように整理できる。
\dfrac{d}{dt}\dfrac{\partial f}{\partial x(t)'} = \dfrac{dx(t)}{\sqrt{dx(t)^2 + dy(t)^2}} = 0\\
\dfrac{d}{dt}\dfrac{\partial f}{\partial x(t)'} = \dfrac{dy(t)}{\sqrt{dx(t)^2 + dy(t)^2}} = 0\\
よって、以下の2つの連立方程式を解けばよいということになる。
\dfrac{dx(t)}{\sqrt{dx(t)^2 + dy(t)^2}} = A, \dfrac{dy(t)}{\sqrt{dx(t)^2 + dy(t)^2}} = B\\
連立方程式を解くと以下になる。
\begin{cases}
\dfrac{dx(t)}{y(t)} = A
\\
\dfrac{dy(t)}{y(t)} = B
\end{cases}
\\
=\begin{cases}
dx(t) = Ay(t)
\\
dy(t) = By(t)
\end{cases}
次に、変化率を求めるため辺々の比を取る
\begin{cases}
dx(t) = Ay(t)
\\
dy(t) = By(t)
\end{cases}
\\
=\dfrac{dx(t)}{dy(t)}=\dfrac{Ay(t)}{By(t)}
\\
=\dfrac{dx(t)}{dy(t)}=\dfrac{A}{B}
よって、
B \cdot dx(t) = A \cdot dy(t)
最後に両辺を$t$で積分すると
Ay = Bx + c
となり、直線の方程式になる。なお、$A, B, C$は定数である。