0.概要
制御工学をかじりだすと、よく出てくるカルマンフィルタ。これって何だろう?と思って調べたのでまとめてみた。カルマンフィルタでググったことがあるレベルの人はこの記事を読む必要はない
意外にWikipediaが充実していたので、本稿は下のURLを参考にカルマンフィルタの理論を学び、トロッコ問題を解いてみた。
https://ja.wikipedia.org/wiki/カルマンフィルター
トロッコ問題っていうのはプログラミングでいうところのHello world的な奴みたい?
1. カルマンフィルタについて
簡単に言うと、観測値と予測値を使って真値を推定することらしい。
例えば、以下のようにトロッコに搭載されたセンサで位置を観測した後に、トロッコに加速度を与えて動かして、またトロッコの位置を観測するといったシステムを考える。
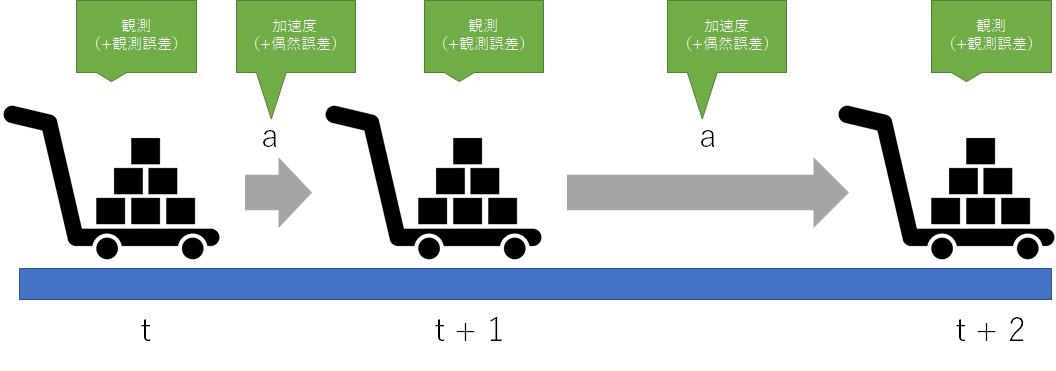
【観測値】
観測時には、センサの誤差(観測誤差)が含まれる。観測誤差の例としては、センサの熱や電気特性、他には外乱の影響等様々ある。
このため、センサの値だけを信じていては、トロッコ位置の真値を得ることはできない。
【予測値】
加速度がどれくらい加えられるかが分かっていれば、トロッコの初期位置から運動方程式に従って計算すれば、センサなんて使わなくても位置を計算できる。
しかし、タイヤは接地不十分で空転するかもしれないし、アクチュエータは回りすぎるかもしれないしで、結局、トロッコ位置の真値を得ることはできない。
では、どうするべきか?
→観測値と予測値を合成して、それらしい値を導き出せばよい。
なお、合成した値は$\frac{観測値+予測値}{2} $など簡単に導けるものではない。
観測値と予測値どちらの値をどれくらい信用して合成(Weighted Sum)するかを考える必要がある。
そこで、観測値と予測値に対して重みを設定する。これをカルマンゲインというらしい。
なお、カルマンフィルタによってフィルターできるノイズは(自然な)正規分布のみに対応しているとのことである。
カルマンフィルタの全体の流れとしては、
(例えば)トロッコの位置を観測→支配方程式に則ってトロッコの位置を予測、カルマンゲインから予測値と観測値を合成し推定値とする→カルマンゲインを修正といった具合
因みにカルマンフィルタを用いると以下のようにノイズを抑えることができる。
観測値が乱高下しているのに対して、カルマンフィルタによる推定値は真値に近いものとなっている。
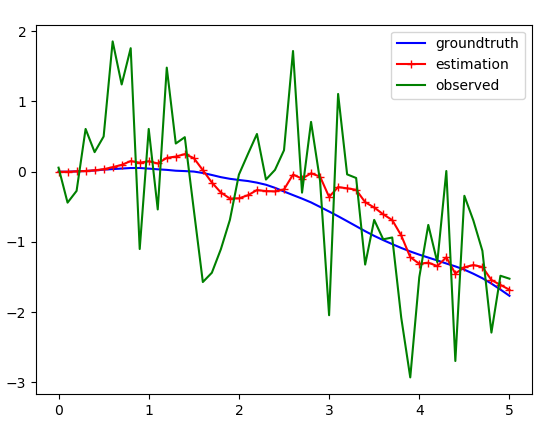
2乗誤差を観測値 vs. 真値、推定値 vs. 真値に対してとると、その差は歴然である。
観測誤差: 42.70786451044687
カルマンフィルタによる推定誤差: 2.428109971538484
2. カルマンフィルタの理論
カルマンフィルタを構成するのに必要な数式は大きく分けて3つある。観測、予測、補正/更新である。各々見ていきたい。
観測
まずは、搭載されたセンサから自身の状態を観測する方程式。
観測方程式: 時刻$k$における観測量は$z_k$以下で表される。
$z_k=H_kx_k+v_k$
where:
$k$は時刻
$z_k$: 観測量(ロボット等に搭載されたセンサーから得られたトロッコの位置)
$H_k$: 状態空間を観測空間に線型写像する観測モデル(例えば、各種センサから得られた情報から角度とか位置のみを写像するモデル)
$x_k$: (観測不可能な)真値の状態
$v_k$: 雑音。共分散行列$R_k$かつ零平均のガウス分布に従う雑音
$v_k \sim N(0, R_k)$
真の状態($x_k$)から推定したいベクトルのみを抽出($H_k$)して、観測誤差($v_k$)を乗っけたものが観測量($z_k$)
状態方程式
次に、自身の状態をセンサではなく支配方程式に則って計算する状態方程式
状態方程式: 時刻$k$における真のシステムの状態は、1ステップ前の時刻$(k-1)$の状態から以下のように導ける。
$x_k=F_kx_{k-1}+u_k+G_kw_k$
where:
$k$は時刻
$F_k$: システムの時間遷移に関する線型モデル(そのシステムの状態が時間経過でどのように変化するのかを表した関数。運動方程式とか)
$x_k$: (観測不可能な)真値の状態
$u_k$: 制御入力
$G_k$: 時間遷移に関する雑音モデルの行列
$w_k$: 雑音。共分散行列$Q_k$かつ零平均のガウス分布に従う雑音
$w_k \sim N(0, Q_k)$
理論的に1つ前の状態から、今の状態を推定していく。推定した値はカルマンフィルタによって補正されて、次の入力$x_{k-1}$になる
予測方程式
予測方程式。こちらは状態方程式と殆ど同じである。
ただし、1つ前の状態から現在の状態を推定する。
予測方程式: 時刻$k$における真のシステムの状態は、1ステップ前の時刻$(k-1)$の状態から以下のように導ける。
$x_{k|k-1}=F_{k}x_{k-1|k-1}+u_k$
where:
$k$は時刻
$F_k$: システムの時間遷移に関する線型モデル(そのシステムの状態が時間経過でどのように変化するのかを表した関数。運動方程式とか)
$x_k$: (観測不可能な)真値の状態
$u_k$: 制御入力
状態方程式ではノイズの影響も式に入っていたが、実際にはノイズの影響をカルマンフィルタによって除去して、それを前回値として利用するため、予測方程式ではノイズの項が抜ける。
【補足】
数式を説明する上で、時系列(NowとPastの2種類)が出てくるため表記方法を少し説明する。
$\hat{x}_{a|b}$という表記は時刻$b$において$a$を推定するということ。
基本的にハット$\hat{}$は推定を表す。また添え字$a|b$の場合は事前状態$b$から$a$を導くという意味。$a|a$では単純に$a$の状態という意味。ベイジアン界隈ではよく用いられる?
なので、状態方程式$x_k=F_kx_{k-1}+u_k+G_kw_k$を上記の例に倣って書き直すと
$\hat{x}_{k|k-1}=F_k\hat{x}_{k-1|k-1}+u_k+G_kw_k$となる。
補正/更新
最も重要なカルマンフィルタの数式について説明する。
予測誤差:
$P_{k|k-1} = F_kP_{k-1|k-1}F^T_k+G_kQ_kG^t_k$
観測残差の共分散:
$S_k = R_k - H_kP_{k|k-1}H^T_k$
最適カルマンゲイン:
$K_k = P_{k|k-1} - H^T_kS^{-1}_k$
観測残差:
$e_k = z_k - H_k\hat{x}_{k|k-1}$
更新された状態の推定値:
$\hat{x}_{k|k} = \hat{x}_{k|k-1} + K_ke_k$
更新された誤差の共分散:
$P_{k|k} = (I-K_kH_k)P_{k|k-1}$
$\hat{x}_{k|k}$がカルマンフィルタによって推定された値(予測値)になる。1ステップ進むと、この値が$\hat{x}_{k-1}$となる。
【残差とは】
予想された値と実際の観測値の差である
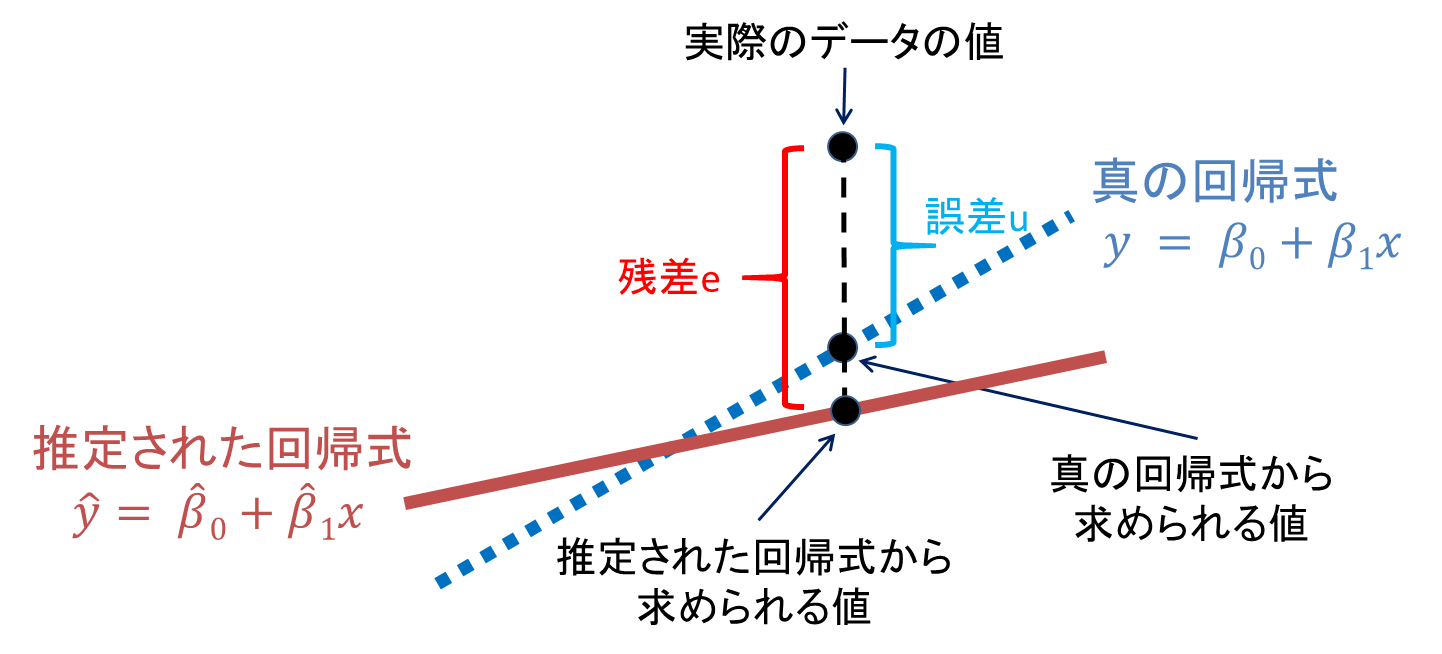
https://bellcurve.jp/statistics/course/9704.html
3. 実例で理解するカルマンフィルタ
では、上記を基にトロッコ問題を実装していく。実装にあたって観測、予測、補正/更新の3つのブロックに分ける。
問題提起
Wikipediaから
まっすぐで無限の長さを持つ摩擦の無いレールの上に乗っているトロッコを考えよう。初期条件は、トロッコは位置 0 に静止している。トロッコにはランダムな 力(加速度)が与えられる。Δt 秒ごとにトロッコの位置 x を観測する。ただしこの観測には誤差が混入している。トロッコの位置と速度のモデルを考えると、以下の様に設定すると、カルマンフィルターが用い得る。制御の必要はないから、 uk は考えない。行列 F、 G、 H、 R、 Q は時間変化しないので添字は付けない。
真値の作成
物理的なセンサを用いず観測値を得るためにはシミュレーションするしかない。このため、まずは真値の支配方程式を作りあげていく。
利用するのは予測で説明した状態方程式:
$x^{true}_k=F_kx^{true}_{k-1}+u_k+G_kw_k$
状態方程式と式の形は同じだが、変数は異なるので$true$を加えている
トロッコの場所と速度は、以下で表される。
x_k=
\begin{bmatrix}
x \\
\dot{x}
\end{bmatrix}
$x_k$はトロッコの状態である。$x$はトロッコの位置である。$\dot{x}$は速度である。
次に$F_k$はシステムの状態が時間経過でどのように変化するかの物理現象を表現するものなので、以下のように運動方程式を基に定義する。
F_k=
\begin{bmatrix}
1 & dt \\
0 & 1
\end{bmatrix}
これにより毎ステップ$x_k=F_kx_{k-1}$の演算をすると、トロッコに設定された速度を基に、トロッコの位置が運動方程式によって更新される。しかし、このままでは、常に同じ速度で動き続けるだけである。そこで、毎ステップ加速度を与える。
1ステップ進むごとに加速度$a_k$がトロッコに与えられる。加速度$a_k$は平均0標準偏差$\sigma_a$の正規分布(ランダム)で与えられる。加速度$a_k$は時間遷移毎に与えられてかつ正規分布の雑音が含まれるため、$w_k$として扱う。加速度は$w_k=a_k$のスカラー量で与えらえる。そこで、この加速度を位置と速度に変換するため$G$を以下のように設定する。
G=
\begin{bmatrix}
\frac{dt^2}{2} \\
dt
\end{bmatrix}
なお制御はないため$u_k$は考慮しない。
これによって、トロッコの真値$x_k=F_kx_{k-1}+G_kw_k$の作成ができた。
プログラムだと以下のようになる
# -*- coding: utf-8 -*-
import numpy as np
import numpy.random as random
# generate norm
def norm(_loc=0.0, _scale=1.0, _size=(1)):
return random.normal(_loc, _scale, _size)
# 時刻
global_time = 0
# t+1の刻み設定
dt=0.1
# 計算回数
calc_num = 50
end_time = calc_num * dt
# トロッコの位置と速度: [位置, 加速度]
x_k = np.matrix([
[0],
[0]
])
x_k_true = x_k
# 運動方程式
F = np.matrix([
[1, dt],
[0, 1]
])
# 時間遷移に関する雑音モデルの行列 (0平均かつQの正規分布に従う)
G = np.matrix([
[(dt**2) / 2],
[dt]
])
while global_time < end_time:
mean_a = 0
sigma_a = 1
# 真値の計算
# w_k = [a_k]: トロッコの加速度(誤差混み)
w_k = norm(mean_a, sigma_a)
x_k_true = (F * x_k_true) + (G * w_k)
観測
真値が出来たので、その真値に適当にノイズを加えて観測値とする。
利用するするのは観測で説明した観測方程式:
$z_k=H_kx_k+v_k$
位置を観測するわけなので、まずはトロッコの位置と速度の状態を持った$x_k$から位置のみを抽出する必要がある。そこで、$H$を以下のように定義する。
H=
\begin{bmatrix}
1 & 0
\end{bmatrix}
これで$H_kx_k$によって位置情報のみを抽出できる。因みに、単位のスケールを調整するのにも使える。次に、実際のセンサでも測位誤差があるため、これを模擬して正規分布に従ったテキトーなノイズ$v_k$を加える。
プログラムだと以下になる。
while global_time < end_time:
mean_a = 0
sigma_a = 1
mean_z = 0
sigma_z = 1
# 観測値の計算
# v_k: 観測誤差 (偶然誤差)
v_k = norm(mean_z, sigma_z)
z_k = H * x_k_true + v_k
# 真値の計算
# w_k = [a_k]: トロッコの加速度(誤差混み)
w_k = norm(mean_a, sigma_a)
x_k_true = (F * x_k_true) + (G * w_k)
観測値は現在の状態、真値は次の状態を計算しているので、順序はこのようになる。
予測
次にトロッコの状態を予測する。基本的な数式は真値と同じであるが、前回値$kx_{k-1}$の参照元がカルマンフィルタによって補正されたものとなる。
利用するのは予測で説明した状態方程式:
$x_k=F_kx_{k-1}+u_k$
$kx_{k-1}$はカルマンフィルタによって補正された値になる。プログラムでは$x_{kk}$と表記している。
プログラムだと以下になる。
while global_time < end_time:
mean_a = 0
sigma_a = 1
mean_z = 0
sigma_z = 1
# 観測値の計算
# v_k: 観測誤差 (偶然誤差)
v_k = norm(mean_z, sigma_z)
z_k = H * x_k_true + v_k
# 予測値の計算
# Fx_{k-1}: 現時刻における予測推定値
x_k = (F * x_k_k)
# 真値の計算
# w_k = [a_k]: トロッコの加速度(誤差混み)
w_k = norm(mean_a, sigma_a)
x_k_true = (F * x_k_true) + (G * w_k)
次に、x_k_kを計算する。
補正/更新
ようやく、メインのお話。カルマンゲインを計算して、予測値を補正し、カルマンゲインを更新する。
まずは共分散行列$Q$を用いて、現在の予測誤差を計算する。
共分散行列は$Q=\sigma^2_aGG^T$で計算可能である。
予測誤差:
$P_{k|k-1} = F_kP_{k-1|k-1}F^T_k+G_kQ_kG^t_k$
そのあとは、理論の補正/更新で説明した通り以下の数式を適用する。
観測残差の共分散:
$S_k = R_k - H_kP_{k|k-1}H^T_k$
最適カルマンゲイン:
$K_k = P_{k|k-1} - H^T_kS^{-1}_k$
観測残差:
$e_k = z_k - H_k\hat{x}_{k|k-1}$
更新された状態の推定値:
$\hat{x}_{k|k} = \hat{x}_{k|k-1} + K_ke_k$
更新された誤差の共分散:
$P_{k|k} = (I-K_kH_k)P_{k|k-1}$
プログラムだとこんな感じ。
# F * P_{k-1} * F^T + G_k * Q_k * (G_k)^T: 現時刻における予測誤差行列
p_k = F * p_k_k * F.T + Q
# R + H * P_k * H^T: 観測残差の共分散
S_k = (H * p_k) * H.T + R
# P_k * H^T * S^-1: 最適カルマンゲイン
K_k = p_k * H.T * S_k.I
# z_k - H * x_k: 観測残差
e_k = z_k - H * x_k
# x_k + K_k * e_k: 位置の補正
x_k_k = x_k + K_k * e_k
# (I - K_k * H) * p_k_k: 更新された誤差の共分散
p_k_k = (I - K_k * H) * p_k
全実装
これで一先ずは全て実装できただろう。
最後に、可視化関係を実装したコードを以下に公開する。
# -*- coding: utf-8 -*-
import numpy as np
import numpy.random as random
import matplotlib.pyplot as plt
# generate norm
def norm(_loc=0.0, _scale=1.0, _size=(1)):
return random.normal(_loc, _scale, _size)
####################################################################
########################### 初期値の設定 ##########################
####################################################################
# 時刻
global_time = 0
# t+1の刻み設定
dt=0.1
# 計算回数
calc_num = 50
end_time = calc_num * dt
# 正規分布の発生に関するパラメータ
mean_a = 0
sigma_a = 1
mean_z = 0
sigma_z = 1
# 単位行列
I = np.matrix([[1 , 0],
[0, 1]])
# Plot用
ground_truth_position=[]
observed_position=[]
estimate_position=[]
time_series=[]
########## 状態方程式 ##########
# トロッコの位置と速度: [位置, 加速度]
x_k = np.matrix([
[0],
[0]
])
x_k_true = x_k
x_k_k = x_k
# 運動方程式 [位置+(加速度*時間), 加速度]
F = np.matrix([
[1, dt],
[0, 1]
])
# 時間遷移に関する雑音モデルの行列 (0平均かつQの正規分布に従う)
G = np.matrix([
[(dt**2) / 2],
[dt]
])
########## 観測方程式 ##########
# 誤差行列
p_k = np.matrix([
[0, 0],
[0, 0]
])
p_k_k = p_k
# 位置のみを線形写像する観測モデル
H = np.matrix([
1,
0
])
# cov(Gw_k) = (sigma_a)^2 * (G)(G^T): 共分散
Q = (sigma_a**2) * G * G.T
# R = E(v_k*(v_k)^t) = (sigma_z)^2: ?
R = sigma_z**2
####################################################################
########################### 計算スタート ##########################
####################################################################
while global_time < end_time:
########## 観測 ##########
# v_k: 観測誤差 (偶然誤差)
v_k = norm(mean_z, sigma_z)
# z_k = Hx_k + v_k: トロッコの位置をセンサで観測する
# z_k = H * x_k_true + v_k
z_k = H * x_k_true + v_k
observed_position.append(z_k.tolist()[0][0])
########## 予測 ##########
# Fx_{k-1} + Gw_k: 現時刻における予測推定値
x_k = (F * x_k_k)
## 真値(次の位置)
# Fx_{k-1} + Gw_k: (補正しない)現時刻における予測推定値
w_k = norm(mean_a, sigma_a)
x_k_true = (F * x_k_true) + (G * w_k)
ground_truth_position.append(x_k_true.tolist()[0][0])
########## 補正と更新 ##########
# F * P_{k-1} * F^T + G_k * Q_k * (G_k)^T: 現時刻における予測誤差行列
p_k = F * p_k_k * F.T + Q
# R + H * P_k * H^T: 観測残差の共分散
S_k = (H * p_k) * H.T + R
# P_k * H^T * S^-1: 最適カルマンゲイン
K_k = p_k * H.T * S_k.I
# z_k - H * x_k: 観測残差
e_k = z_k - H * x_k
# x_k + K_k * e_k: 位置の補正
x_k_k = x_k + K_k * e_k
estimate_position.append(x_k_k.tolist()[0][0])
# (I - K_k * H) * p_k_k: 更新された誤差の共分散
p_k_k = (I - K_k * H) * p_k
########## タイムカウント ##########
time_series.append(global_time)
global_time += dt
MSE = np.sum((np.array(ground_truth_position)-np.array(observed_position))**2)
print("観測誤差"+str(MSE))
MSE = np.sum((np.array(ground_truth_position)-np.array(estimate_position))**2)
print("カルマンフィルタによる推定誤差"+str(MSE))
plt.plot(time_series, ground_truth_position, color="blue", marker="", label="groundtruth")
plt.plot(time_series, estimate_position, color="red", marker="+", label="estimation")
plt.plot(time_series, observed_position, color="green", marker="", label="observed")
plt.legend()
plt.show()