複素数の定義
複素数の定義
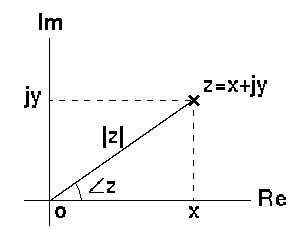
z=x+iy
ここで、$x$及び$y$は
x=\cos\theta \\
y=\sin\theta
と定義され、実数成分が$x$の$cos$、虚数成分が$y$の$sin$である。
極形式への変換
複素数は円のある点を表すため、半径の長さと角度を持った極形式への変換が可能である。
半径の長さ、すなわち絶対値$r$は、次のように示される。
r = |z| = \sqrt{x^2 + y^2}
角度すなわち、偏角$\theta$は次のように示される。
\theta=\angle{Z}=\tan^{-1}{(\dfrac{y}{x})}
これを$z$まわりに整理すると
z=r(\cos{\theta} + i\sin{\theta}) = r\cdot\exp^{i\theta} \\
= re^{i\theta}
となる。
複素数の制約
複素数上では座標移動の際に象限を跨ぐことを表現するため、以下の制約がある。
i^2 = -1
共役複素数
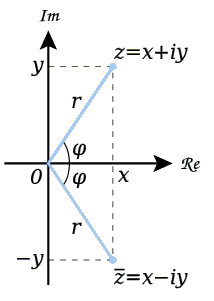
虚数部を反数にすることで得られる。
\overline{z}=x-iy
実軸対称変換を行っているだけである。
複素数の掛け算
複素数の掛け算は$i^2=-1$という制約の基、$x$と$w$の複素数(実数: $^{re}$、虚数: $^{im}$)が与えられた場合、以下のように定義される。
xw = (x^{re}+x^{im}_{i})(w^{re}+w^{im}_{i}) \\
= x^{re}w^{re} + x^{im}_{i}w^{re}+x^{re}w^{im}_{i}+x^{im}_{i}w^{im}_{i}\\
= x^{re}w^{re} + x^{im}_{i}w^{re}+x^{re}w^{im}_{i}+(-1\cdot(x^{im}w^{im})) \\
= (x^{re}w^{re}-x^{im}w^{im}) + (x^{re}w^{im} + x^{im}w^{re})_{i}
$i^2=-1$といった制約があるおかげで回転を表現できる。$im$同士を掛けることで90度回転する。
すなわち、$im * im * im * im = -1 * -1 = 1$となり、360度の回転をする。
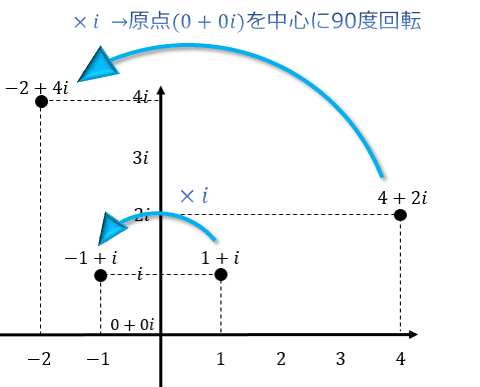
複素数を用いた回転(https://atarimae.biz/archives/500)
このように$im$を掛けるだけで各象限間を遷移することができる。
極形式で表現しなおすと、
複素数の掛け算が偏角の足し算と絶対値の掛け算であることが容易に理解できる。
まず、複素数の掛け算は以下である。
xw = (x^{re}+x^{im}_{i})(w^{re}+w^{im}_{i})\\
各変数を極形式へ変換すると以下になる。
x = |x|(\cos{\theta_{x}} + i \sin{\theta_{x}})
w = |w|(\cos{\theta_{w}} + i \sin{\theta_{w}})
次に極形式で掛け算を行う。
xw = |x|(\cos{\theta_{x}} + i \sin{\theta_{x}}) \cdot |w|(\cos{\theta_{w}} + i \sin{\theta_{w}})\\
=|x||w|(\cos{\theta_{x}}\cos{\theta_{w}} - \sin{\theta_{x}}\sin{\theta_{w}}) \cdot
i(\cos{\theta_{x}}\sin{\theta_{w}}+\sin{\theta_{x}}\cos{\theta_{w}}) \\
=|x||w|(\cos{(\theta_{x}+\theta{w})}+ i\sin{(\theta_{x}+\theta{w})})
よって、複素数の掛け算とは偏角の足し算$\theta_{x}+\theta{w}$及び絶対値の掛け算$|x||w|$から構成されている。
計算
以下を計算する。
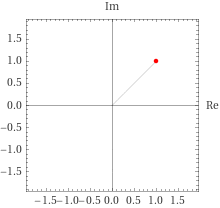
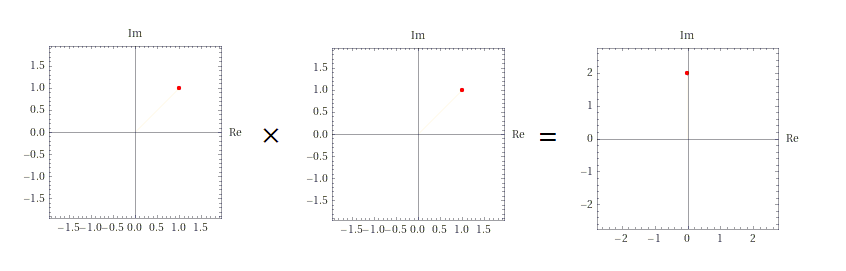
z \cdot z = (1+1i) \cdot (1+1i)
まず変数を極形式にする。絶対値を以下のように求める。
r = |z| = \sqrt{x^2 + y^2}\\
= \sqrt{2}\\
= 1.4142...
次に偏角を求める。
\theta=\angle{Z}=\tan^{-1}{(\dfrac{y}{x})} \\
=\tan^{-1}{1}\\
=\dfrac{\pi}{4}=45 dgree
すなわち、
= 1.4142e^{i\dfrac{\pi}{4}}
となる。グラフ化するとこのような形。
次に掛け算する。
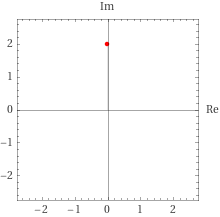
z = (1+1i) \cdot (1+1i)
複素形式で解くと、
z = (x^{re}w^{re}-x^{im}w^{im}) + (x^{re}w^{im} + x^{im}w^{re})_{i}\\
= (1*1 - 1*1) + (1*1 + 1*1)_{i}\\
= 0+2_{i}
となり、グラフで表現すると以下のようになる。
極形式だと、
r = \sqrt{x^2 + y^2} = \sqrt{4} = 2\\
\theta=\tan^{-1}{(\dfrac{y}{x})} = \tan^{-1}(\dfrac{4}{0})= \tan^{-1}(\infty) = \dfrac{\pi}{2}=90 dgree \\
となる。複素数の掛け算が偏角の足し算と絶対値の掛け算であることが確認できた。
複素数の差分(位相差)
複素数の差分を取る。これすなわち、干渉処理/位相差ということである。
位相差を求めるためには以下の計算を行う。
d = z_{a} \cdot \overline{z_{b}}
ここで各変数は以下とする。
z_{a}=x+iy\\
z_{b}=x+iy \\
これすなわち、共役を取り、実軸対象にしてから掛け算（偏角を足し算）しているだけである。
このため、$z_{a}==z_{b}$であれば位相差なしで偏角は0度となる。
計算
以下の位相差を取る。
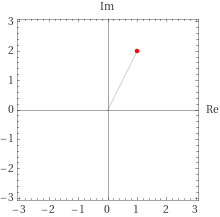
z_{a}=1+2_{i}\\
r=2.23607\\
\theta=63.4349 degree
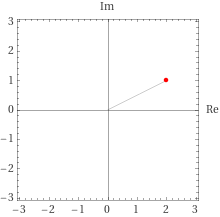
z_{b}=2+1_{i}
r=2.23607\\
\theta=26.5651 degree
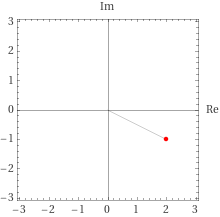
次に$\overline{z_{b}}$を求める。
\overline{z_{b}}=z_{b}=2-1_{i}
最後に位相差を求める。
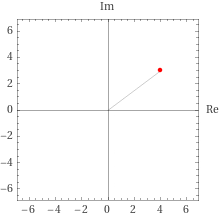
d = z_{a} \overline{z_{b}}=(1+2_{i})(2-1_{i})\\
=4+3_{i}
極形式の場合は以下である。
r=5\\
\theta=36.8699 degree
これで、差分が計算できた。ただ偏角同士の差分を求めているだけである