0. 概要
ベイズ推定を行うにあたって基礎的な理論である事前分布、事後分布を説明し、実際に逐次ベイズ推定の計算を行っていく。
1. ベイズの定理
まず良く目にするベイズの定理は以下である。
P\left( B| A\right) = \dfrac{P\left( A| B\right)P(B)}{P(A)}
これをラプラスがベイズ確率に昇華したものが以下である。
P\left( \theta| y\right) = \dfrac{P\left( y| \theta\right)P(\theta)}{P(y)}
確率変数$\theta$を明示したこと以外は全くもって同じ式である。
ここで、各変数$P$は条件付き確率、$\theta$は確率、$y$はデータであり、
$P\left( \theta| y\right)$は事後分布、$P\left( y| \theta\right)$は尤度、$P(\theta)$は事前分布、$P(y)$はそのデータが生じた確率である。
#2. 尤度
尤度を示す$P\left( y| \theta\right)$は、$\theta$の条件の元、$y$が発生する確率$P$という風に読むことができる。
例
まず、
「$\dfrac{1}{2}$の確率で裏、表が出るコインを3回投げた時、表、表、表と続けて出た際の確率はいくつか」
という例題を考える。
ここで、各変数は以下の通りである(0=表、1=裏として表記している)。
\theta=\dfrac{1}{2}\\
y=\left\{ 0,0,0\right\}
次に尤度を求める。純粋に確率の計算をすればよいので、
P\left( y| \theta\right)=P\left(y=\left\{ 0,0,0\right\}| \theta=\dfrac{1}{2}\right)=(\dfrac{1}{2})^{3}=\dfrac{1}{8}
のようになる。慣れ親しんだ確率の計算である。
捕捉
尤度の計算の定義としては以下である。
P(y|\theta)=p^{y}(1-\theta)^{1-y}
今回の例だと$y$が3回独立事象で発生するので各確率を掛け算すればよく、以下のように展開できる。
P(y|\theta)=P(y_1|\theta)P(y_2|\theta)P(y_3|\theta)\\=\prod_{i=1}^3P(y_i|\theta)\\=\prod_{i=1}^3p^y_i(1-\theta)^{1-y_i}
3. 事後分布と事前分布
事後分布
事後分布は$P\left( \theta| y\right)$である。ベイズの定理は以下であるように、
P\left( \theta| y\right) = \dfrac{P\left( y| \theta\right)P(\theta)}{P(y)}
事後分布は事後分布=尤度×事前分布÷yが発生する確率から求められる。
事後分布は尤度$P\left( y| \theta\right)$と順序が逆になっているだけである。尤度では、ある確率$\theta$に従って、ある事象$y$が発生する確率を求めていた。
しかし、ある確率($\theta$)が未知で、起こった事象$y$しか分からないことの方が世の中多い。例えば、商店街のガラポン等…である。
これすなわち、観測された事象$y$から、それがどれくらいの確率で発生する$\theta$なのかを求めることである。
事前分布
事前分布$P(\theta)$とは、$\theta$が複数あると考えた場合に、ある$\theta$を引く確率$P(\theta)$である。
例えば、商店街の歳末ガラポン会場に行ったとする。ガラポンは3台あり、ハワイ旅行が出る確率$\theta$は1台目は0%、2台目は0%、3台目は1%であったとする。この時、どのガラポンを好んで選ぶかが事前分布である。3台目はいつも空いており待ち時間がないので選択される確率が高いとする。よって1台目を選ぶ確率は10%、2台目を選ぶ確率は10%、3台目を選ぶ確率は80％としたとする。これを事前分布という。
同時分布
同時分布は尤度×事前分布から得られる。先ほどの例題から尤度と事前分布は以下の通りである。
尤度: 1台目0%、2台目0%、3台目1%
事前分布: 1台目10%、2台目10%、3台目80%
よって、同時分布は
同時分布: 1台目0%×10%、2台目0%×10%、3台目1%×80%
である。
4. 計算
例題
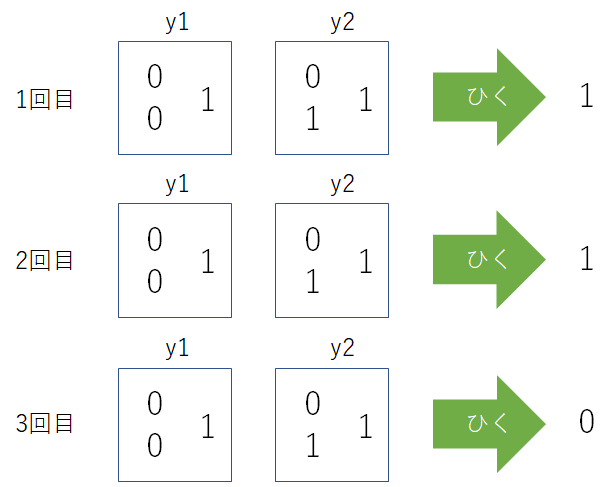
2つのボックスの中に0及び1が入っている。目隠しをしてボックスを1つ選び数字を引いた。
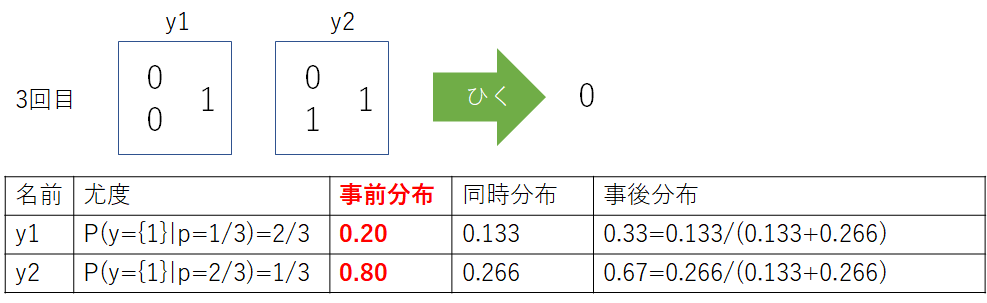
これを3回繰り返した結果1, 1, 0という数列を得た。この時、ボックス2($y_{2}$)を選択した確率は?
ここで、$y_{1}$は$\dfrac{1}{3}$で1が混入されており、$y_{2}$は$\dfrac{2}{3}$で1が混入されている。
また、目隠しをされている状態なので、各ボックスを選択する確率はランダムの$\dfrac{1}{2}$である。
4.1. ベイズ推定(事後分布を求める)
事後分布は事後分布=尤度×事前分布÷yが発生する確率であり、
すなわち事後分布=同時分布÷yが発生する確率とも書けるため、
まずは以下のように同時分布を求める。
各ボックスの尤度はボックスの確率から求めることが出来る。事前分布はボックスをランダムに選ぶので$\dfrac{1}{2}$である。その結果、同時分布はそれぞれ$\dfrac{1}{27}$、$\dfrac{2}{27}$となった。
ここまでで、以下の事後分布の内、P(y)以外は分かった。
P\left( \theta| y\right) = \dfrac{P\left( y| \theta\right)P(\theta)}{P(y)}
P(y)は、$y$が起こった場合の$p$の分布のため、表の同時分布を全て足せばよい。
よって、$\dfrac{3}{27}$である。
最終的に、各$y_1$、$y_2$の確率は
P_{y_{1}} = \dfrac{\dfrac{2}{27}\cdot\dfrac{1}{2}}{\dfrac{3}{27}} = 0.33333 = 33\%
P_{y_{2}} = \dfrac{\dfrac{4}{27}\cdot\dfrac{1}{2}}{\dfrac{3}{27}} = 0.66666 = 67\%
となる。よって、今回の試行の中で$y_2$を選んだ確率は67%である。
4.2. 逐次ベイズ推定
逐次ベイズは名前の通り、ボックスから引いて観測する行為1回ごとに計算を行っていく。
4.1との大きな違いは、2回目引くときには、1回目に計算した事後分布を事前分布として使って計算を行う。
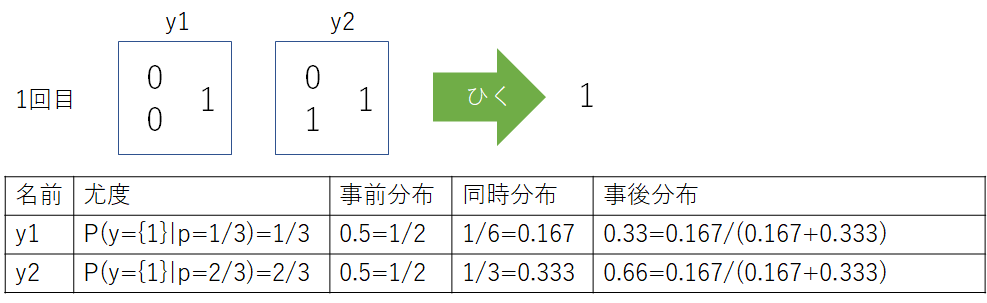
1回目
ここで事前分布は無作為に選ぶので$\dfrac{1}{2}$である。
2回目
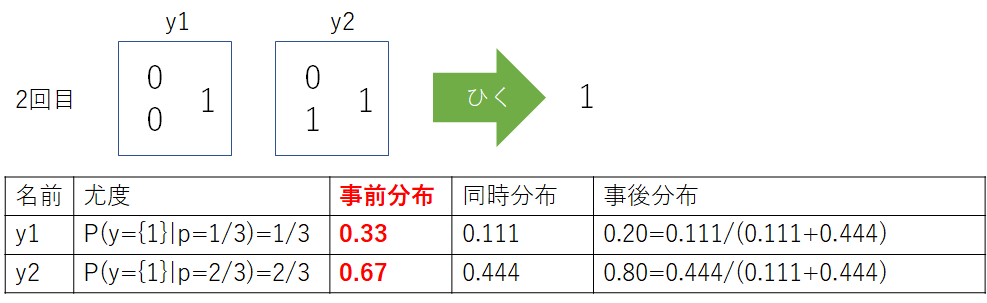
ここで事前分布は1回目の事後分布を事前分布として採用する。
本人は無作為に選んでいるつもりでも、無作為に選んでいない可能性があるため。
3回目
同様に、2回目で計算した事後分布を事前分布として採用して計算する。
最終的に$y_2$を選ぶ確率は67%となった。