Deformable Convolutionに(処理過程を図解及びKerasで実装しながら)入門する

0. 概要

近年、様々と提案されているConvolution技術の1つであるDeformable Convolutionについて入門したいと考える。2017年に初出のこの技術は、頃日提案されている様々なCNNモデルに応用され、重要なキー技術となっている。例えば、Mask R-CNN等にも用いられている。具体的には、これまでのConvolutionは画像全体に対して、大域的かつ均一にフィルタリング処理を行うのにたいして、Deformable Convolution (Deform-Conv)は識別対象の物体に対して局所的に動的にフィルタリングを行う方法である。このため、位置及びスケーリング変化に強いとされる。

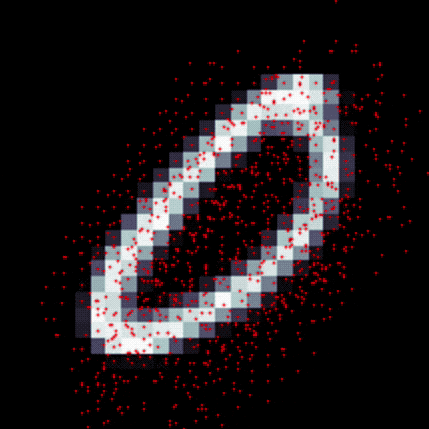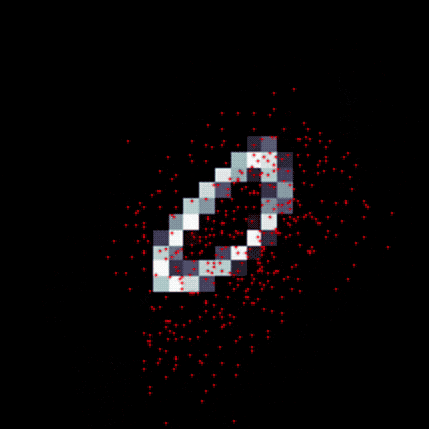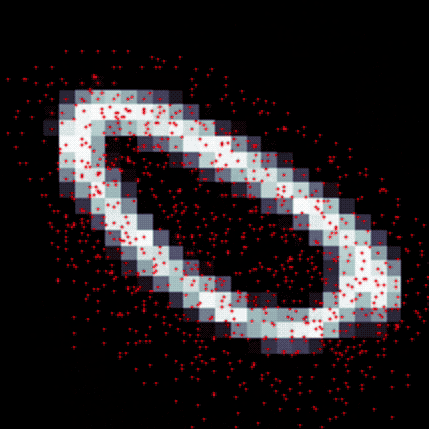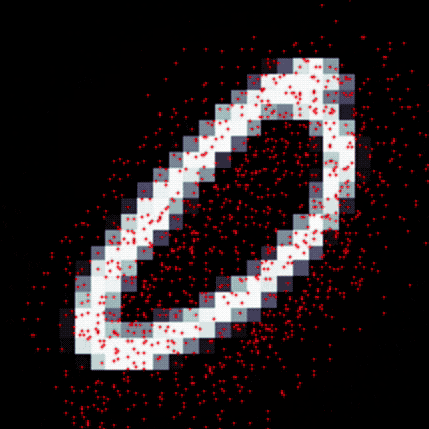
https://arxiv.org/abs/1703.06211

ウェブ上の記事で様々な解説があるものの、その具体的な実装について触れているものは少なく、
論文中の数式を見ただけでは抽象化されすぎており、実装は困難なのではないかと思い処理過程を追っていきたいと考える。

1.0. Deformable Convolutionの仕組み

Deformable Convolutionの仕組みを論文ベースで説明する。

1.1. Deformable Convolutionの概要

これまでAtrous convolutionのようにカーネルの畳み込む距離等を変化させる方法はいくつも提案されてきたが、
これらは入力画像毎に、動的に最適化された畳み込みを提供するわけではない。
このため、対象物にスケールや回転といった処理が加わったものに対して頑健性を提供できていなかった。

そこで、Deformable Convolutionでは次の図のように入力画像毎に、畳み込み位置及び畳み込む距離を最適化する方法を提案している。

緑色が一般的なConvolutionの位置で、それに対して最適化をした結果が青色の矢印である。

図中の(a)が一般的なConvolutionの畳み込みである。これに対して、(b)、(c)、(d)がDeformable Convolutionの一例である。(c)はAtrous convolutionのような畳み込み(カーネル)に見え、最適化の具合によっては、そのような学習も可能ということである。

1.2. Deformable Convolutionの数式

Deformable Convolutionで用いられる数式を説明する。

1.2.1 一般的な畳み込み処理

まずカーネルの受容野のサイズとダイレーションを定義する。難しく考える必要はなく、
受容野=1回の畳み込みで取り入れる領域(カーネルサイズ)、ダイレーション=サンプリングの密度(膨張率)と考えればよい。
例えば、3x3の一般的なカーネルの場合は以下のように定義できる。

R={(-1, -1), (-1, 0), \dots, (0, 1), (1, 1)}

すなわち、これはカーネルの中心座標を(0, 0)としたとき各サンプリング点を以下のように表現しているだけである。

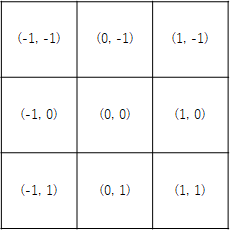
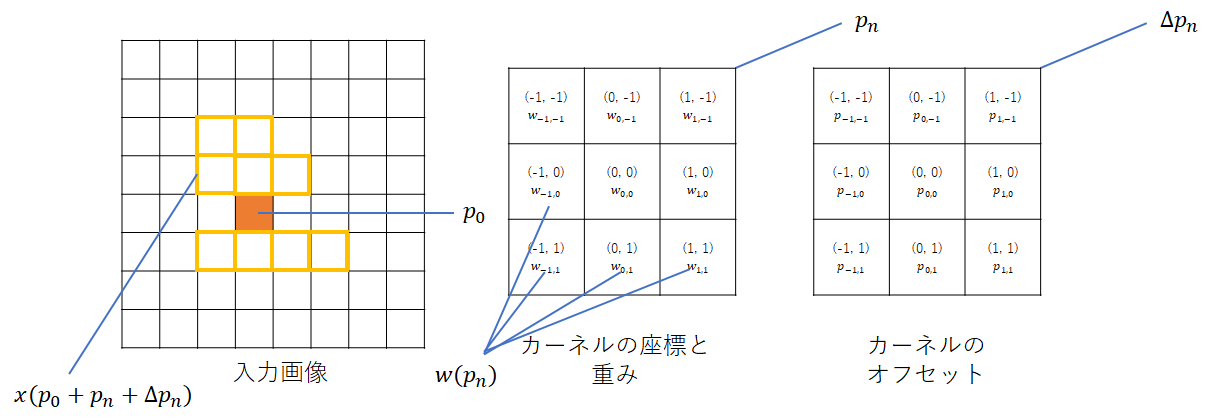
次に、入力画像のあるピクセル$p_0$を中心としたときの、カーネル$w$の畳み込み処理を以下のように定義する。

y(p_0) = \sum_{p_n \in R} w(p_n) \cdot x(p_0 + p_n)

$x$は座標位置からピクセル値を取り出す関数を指している。
これから、$p_n$は入力画像に対してカーネルを畳み込む相対位置を示しているということが分かる。
図示すると以下のようになる。

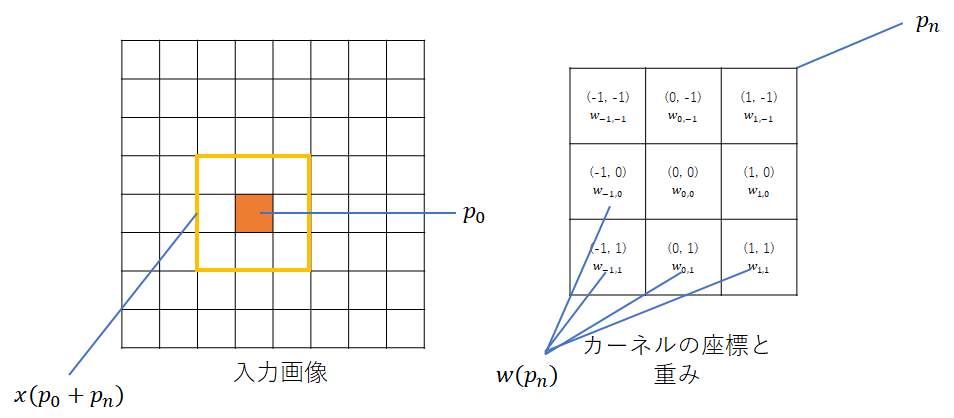
$p_0$が$(3, 4)$の場合、カーネル$w_{-1, -1}$は相対位置$(-1, -1)$のため、入力画像の$x = (3, 4) + (-1, -1)$位置を参照し、それに$w_{-1, -1}$を掛けるという処理が行われる。

1.2.2 Deformableの畳み込み処理(ベース)

Deformable Convolutionは先ほどの$p_n$を工夫して、$x$によって取り出すピクセル値の参照位置を動的に変化させることが目的である。
よって、数式で表現すると以下のようになる。

y(p_0) = \sum_{p_n \in R} w(p_n) \cdot x(p_0 + p_n + \Delta p_n)

$\Delta p_n$で畳み込む位置を動的に変化させている。このため、畳み込む位置を入力画像から得るためには$x(p_0 + p_n + \Delta p_n)$となる。図で表現すると以下のようになる。

なお、元の畳み込む位置からオフセット分(相対距離で)ずらす$\Delta p_n$の各要素を$p_{-1, -1} \dots p_{1, 1}$で表現しているが、最初は0で初期化されているため、学習前は普通の畳み込み処理となる。$p_n$は浮動小数点である。

1.2.3 Deformableの畳み込み処理 (補間)

$p_n$は浮動小数点であるため、整数への丸め込み処理が必要である。
しかし、丸め込んだ結果として、入力画像のあるピクセル値を誤って持ってきてしまうかもしれない。そこで、何らかの補完を用いる。
本家の論文ではバイリニア補完を用いているが、他にも様々な手法が提案されている。よって、入力画像からあるピクセル値を取得するための最終的な式は以下と表現できる。

x(p) = \sum_{q} G(q, p) \cdot x(q) \\
= \sum_{q} G(q, p_0 + p_n + \Delta p_n) \cdot x(q) 

バイリニア補完の場合、qは近傍4点となる。

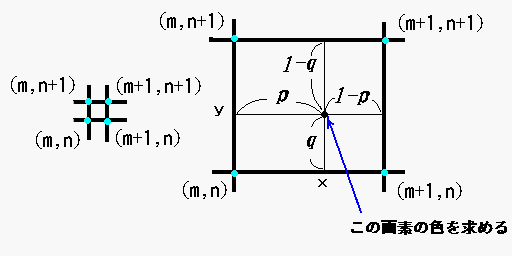
http://www.asahi-net.or.jp/~uc3k-ymd/Sketch/Scale/scale01.html

近傍4点の座標は浮動小数点を切り下げ、切り上げする操作で整数値の4点を得ればよい。

2.0. Deformable Convolutionの実装

ここまでで、Deformable Convolutionがどのような働きをするのかが分かった。これを実装に落とし込んでいく。
また、補完については様々な方法がある点と、本質的な範囲ではないので特に触れない。

2.1. アーキテクチャ

全体のアーキテクチャを以下のように定義する。

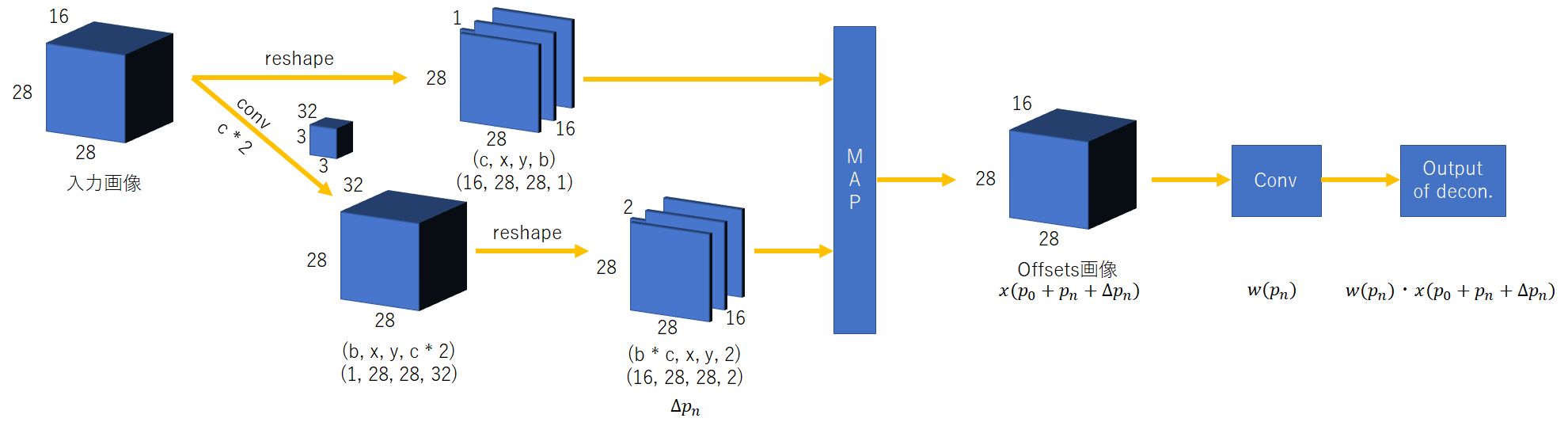
$x(p_0 + p_n + \Delta p_n)$を構築さえすれば、後は一般的な畳み込み処理で演算が可能である。
ようは、$x(p_0 + p_n + \Delta p_n)$で畳み込みを行いたい領域を入力画像から抽出するのである。
そこで、入力画像のあるピクセルが参照されたときに、どこの画素を見に行けばよいのかを参照する参照マトリックスを作る。
これに相当するものが図内のMAPより左側である。$\Delta p_n$と書かれているチャンネルが2となっているが、
これは画像内の座標を2次元で示すためのx及びyを意味する。
よって、入力画像の1チャンネルにあたり、同サイズで2チャンネルのoffsetsが必要になる。

なお、内部のMAP処理は以下のようなっている。簡単のため8x8としている。

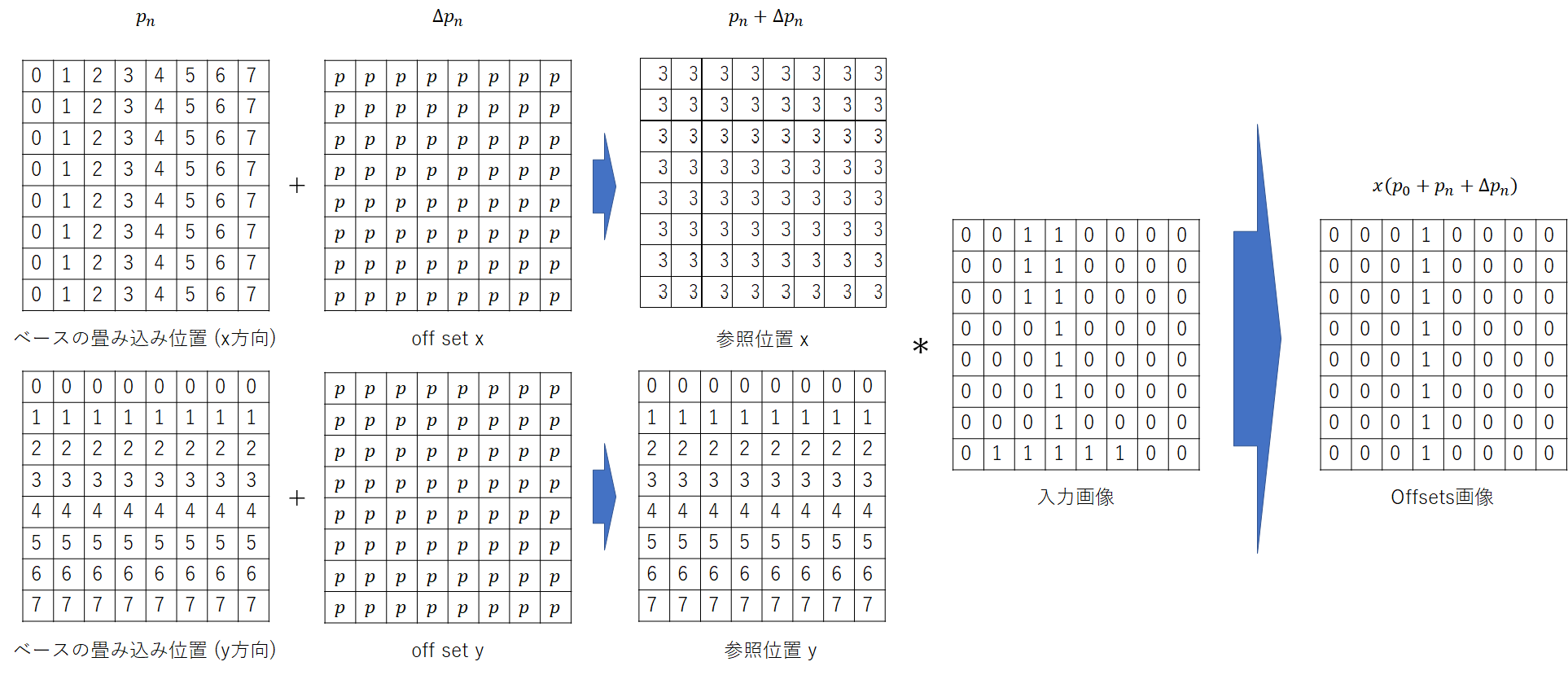
$p$と書かれているパラメータ全てが学習変数である。$p_n$は静的に生成したマトリクス表を用いている。

2.2. 参照マトリクスの生成及びReshaping処理(MAPより左側)

まずアーキテクチャで説明したMAPより左側の処理を構築したいと考える。
やることは単純で、Conv2dを用いて参照マトリクスのx及びyを作る。

class DFConv2D(Layer):
  def __init__(self, **kwargs):
    super(DFConv2D, self).__init__(**kwargs)

  def build(self, input_shape):
    self._conv2d = Conv2D(input_shape[3] * 2, (3, 3), padding='same')
    super(DFConv2D, self).build(input_shape)

  def call(self, x):
    x_shape = x.get_shape()
    offsets = self._conv2d(x)
    offsets = tf.transpose(offsets, [0, 3, 1, 2])
    offsets = tf.reshape(offsets, (-1, int(x_shape[1]), int(x_shape[2]), 2))
    x = tf.transpose(x, [0, 3, 1, 2])
    x = tf.reshape(x, (-1, int(x_shape[1]), int(x_shape[2])))
    #######################################
    x_offset = mapping(x, offsets)
    #######################################
    x_offset = tf.reshape(x_offset, (-1, int(x_shape[3]), int(x_shape[1]), int(x_shape[2])))
    x_offset = tf.transpose(x_offset, [0, 2, 3, 1])
    return x_offset

    def compute_output_shape(self, input_shape):
        return input_shape

2.3. Offsetsに基づいて入力画像から画素を抽出する(MAP内処理)

後は、meshgridを用いて$p_n$を作成し、 $\Delta p_n$を足すだけで終わりである。
足した結果として、浮動小数点が出てくるので、それを丸め込んだりする処理は必要である。

def mapping(input, offsets, order=1):
    input_shape = tf.shape(input)
    batch_size = input_shape[0]
    input_size = input_shape[1]
    offsets = tf.reshape(offsets, (batch_size, -1, 2))
    grid = tf.meshgrid(
        tf.range(input_size), tf.range(input_size), indexing='ij'
    )
    grid = tf.stack(grid, axis=-1)
    grid = tf.cast(grid, 'float32')
    grid = tf.reshape(grid, (-1, 2)) # (size * size, 2)
    grid = tf_repeat_2d(grid, batch_size) # (n, size * size, 2)
    x_y_offsets = offsets + grid
    #########################################################
    mapped_vals = extract(input, x_y_offsets)
    #########################################################
    return mapped_vals

extract関数は入力画像及びoffsetから特定の画素値を抽出する関数である。