0. 概要
SVD (singular value decomposition)は次元削減(Dimensionality Reduction)分野で用いられる技術である。
例えば、患者のあらゆる生体データなどを圧縮して少ない行列で表現したりできる。
機械学習で扱うデータ量が多い場合や、感度解析をしたい場合等に用いる。
以下のスタンフォード大学のレクチャーが非常に分かりやすい。彼もSVDは次元削減テクニックの内の1つといっている。
https://www.youtube.com/watch?v=P5mlg91as1c
1. 理論
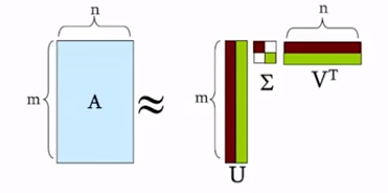
SVDとは、任意$i×j$の実数行列$A$を幾何的に解釈可能な3つの行列の積へと分解することに他ならない。
基本の定理は次式である。
A_{m×n}=U_{m×r}\Sigma_{r×r} V^{T}_{n×r}
各変数の説明は以下である。
$\Sigma$: 正数$\sigma$からなる$r×r$の対角行列で、特異値であり寄与度が高い順にソートされている。固有値からルートを取るだけである。
$U$: $m×r$の直行行列(すなわち、逆行列を計算できる)
また、$A$の左特異ベクトルといい、$m$次元空間における$A$の列の正規直交基底となっている。
$V$: $n×r$の直行行列(すなわち、$U^{T}U=V^{T}V=E$)
また、$A$の右特異ベクトルといい、$n$次元空間における$A$の行の正規直交基底となっている。求めた固有値から固有ベクトルを計算して単位ベクトル化するだけである。
である。
さらに展開すると、次式のように表現できる。
A
=U_{m×r}\Sigma_{r×r} V^{T}_{n×r}\\
=\Sigma _{i}\sigma _{i}u_{i}\circ v^{T}_{i}\\
=\left\{ u_{1},u_{2},\ldots ,u_{i}\right\}
\begin{bmatrix}
\sigma_{1} & & \\
& \sigma _{2} & \\
& & \ddots \\
& & & \sigma _{i}
\end{bmatrix}
\begin{bmatrix}
v^{T}_1 \\
v^{T}_2 \\
\vdots \\
v^{T}_i
\end{bmatrix}
この時、$\Sigma$はソートされているため、$\sigma _{1}\geq \sigma _{2}\geq \dots \geq \sigma _{n}$となっている。
$\Sigma$は対角行列のため、$\Sigma \Sigma^{T}=\Sigma^{2}$となり、各特異値$\sigma$は$AA^{T}$の固有値から平方根を取ったものとなる。
すなわち、$AA^{T}=U \Sigma V^{T}V \Sigma^{T} U^{T} = U\Sigma\Sigma^TU^T$となる。
イメージ的な話:
$\Sigma$は固有値、$V$は固有ベクトル、じゃあ$U$は・・?
ある行列$A$と積をとっても同じ向きになるベクトルが$V$。
$V\Sigma$で$A$と同じ方向のある大きさのベクトルになる。
いわゆる、$A$のデータに見られる共通的な特徴。そして、$U$が主成分(固有値)。
もっと単純に言うと
$U$は列の類似度
$V^T$は行の類似度
$\Sigma$は各類似度の強調度
2. 計算する
SVDで分解する$A$を次のように定義する
A=\begin{bmatrix} 4 & 0 \\ 3 & -5 \end{bmatrix}
Step. 1: $\Sigma$を求める。
まず$A^{T}A$を求める。
A^{T}A=\begin{bmatrix} 4 & 3 \\ 0 & -5 \end{bmatrix}
\begin{bmatrix} 4 & 0 \\ 3 & -5 \end{bmatrix}
=\begin{bmatrix} 25 & -15 \\ -15 & 25 \end{bmatrix}
次に$A^{T}A$から固有値を求める。
(A-\lambda E)=\begin{bmatrix} 25 - \lambda & -15 \\ -15 & 25 - \lambda \end{bmatrix}\\
=(25-\lambda)^{2}-(-15)^2=625-25\lambda-25\lambda+\lambda^{2} - 225\\
= \lambda^{2}-50\lambda+400
次式で$\lambda^{2}-50\lambda+400 = 0$を解き、固有値$\lambda$を解く
\lambda^{2}-50\lambda+400 = 0 \\
=(\lambda^{2}-50\lambda+25^{2}-25^{2})+400 :おもむろに平方完成\\
=(\lambda-10)(\lambda-40) -400 +400\\
=(\lambda-10)(\lambda-40) \\
よって$\lambda=10$、$\lambda=40$が出てきた。
次にこれを固有値から特異値(Singular values)$\sigma_i$に変換する。といっても、ただ固有値のルートを取るだけである。
\sigma_1=\sqrt{40}=6.32456, \sigma_2=\sqrt{10}=3.1623
次に、これを対角行列として配置するが、その際に数値をソートする。今回は$40$の方が大きいのでこちらが上位である。
※ どのようにソートしたか覚えておけば、各要素の寄与率が分かる。
\Sigma=\begin{bmatrix} 6.32456 & 0 \\ 0 & 3.1623 \end{bmatrix},
\Sigma^{-1}=\frac{1}{6.32456 * 3.1623 - 0 * 0}\begin{bmatrix} 3.1623 & 0 \\ 0 & 6.32456 \end{bmatrix}
=\begin{bmatrix} 0.15812 & 0 \\ 0 & 0.31623 \end{bmatrix}
Step. 2: $V$を求める。
固有値が求まったので、次に$V$、これすなわち固有ベクトルを求める。
$\lambda=40$の場合:
次式の固有方程式に従って計算を進めていく。
(A^{T}A - \lambda E)\overrightarrow {x} = 0
求めた$\lambda$を代入して
(A^{T}A - \lambda E)\overrightarrow {x}
=\begin{bmatrix} 25 - 40 & -15 \\ -15 & 25 - 40 \end{bmatrix}
\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}
=\begin{bmatrix} -15 & -15 \\ -15 & -15 \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}
$\overrightarrow {x}$を求める。
\begin{bmatrix} -15 & -15 \\ -15 & -15 \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}
=\begin{bmatrix} 0 \\ 0 \end{bmatrix}
よって、以下の固有ベクトルが求まった。
\begin{bmatrix} -15 & -15 \\ -15 & -15 \end{bmatrix}\begin{bmatrix} 1 \\ -1 \end{bmatrix}
=\begin{bmatrix} 0 \\ 0 \end{bmatrix}
固有ベクトルを扱いやすいよう単位ベクトル化する。
v_1=\frac{1}{L}\begin{bmatrix} 1 \\ -1 \end{bmatrix}
=\frac{1}{\sqrt{(1)^{2}+(-1)^{2}}}\begin{bmatrix} 1 \\ -1 \end{bmatrix}
=\begin{bmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \end{bmatrix}
=\begin{bmatrix} 0.707106 \\ -0.707106 \end{bmatrix}
これで単位ベクトルとなった。
$\lambda=10$の場合:
同様にもう一方の固有ベクトルも求めていく。求めた$\lambda$を代入して
(A^{T}A - \lambda E)\overrightarrow {x}
=\begin{bmatrix} 25 - 10 & -15 \\ -15 & 25 - 10 \end{bmatrix}
\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}
=\begin{bmatrix} 15 & -15 \\ -15 & 15 \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}
$\overrightarrow {x}$を求める。
\begin{bmatrix} 15 & -15 \\ -15 & 15 \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}
=\begin{bmatrix} 0 \\ 0 \end{bmatrix}
よって、以下の固有ベクトルが求まった。
\begin{bmatrix} 15 & -15 \\ -15 & 15 \end{bmatrix}\begin{bmatrix} 1 \\ 1 \end{bmatrix}
=\begin{bmatrix} 0 \\ 0 \end{bmatrix}
固有ベクトルを扱いやすいよう単位ベクトル化する。
v_2=\frac{1}{L}\begin{bmatrix} 1 \\ 1 \end{bmatrix}
=\frac{1}{\sqrt{(1)^{2}+(1)^{2}}}\begin{bmatrix} 1 \\ 1 \end{bmatrix}
=\begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix}
=\begin{bmatrix} 0.707106 \\ 0.707106 \end{bmatrix}
最後に合わせて、$V$とする。
V = \begin{bmatrix} v_1 & v_2 \end{bmatrix}
=\begin{bmatrix} 0.707106 & 0.707106 \\ -0.707106 & 0.707106 \end{bmatrix}
$V^T$は以下である。
V^T
=\begin{bmatrix} 0.707106 & -0.707106 \\ 0.707106 & 0.707106 \end{bmatrix}
Step. 3: $U$を求める。
残すは$U$だけである。まずは次式を変形して、
A_{m×n}=U_{m×r}\Sigma_{r×r} V^{T}_{n×r}
$U=$の形にする。移項すると逆行列になる。直行行列のため、$^T=^{-1}$の関係のであり、移項すると転置が消える/転置になる。
U_{m×r}=A_{m×n}V_{n×r}\Sigma^{―1}_{r×r}
$U$を求める。
U
=\begin{bmatrix} 4 & 0 \\ 3 & -5 \end{bmatrix}
\begin{bmatrix} 0.707106 & 0.707106 \\ -0.707106 & 0.707106 \end{bmatrix}
\begin{bmatrix} 0.15812 & 0 \\ 0 & 0.31623 \end{bmatrix}\\
=\begin{bmatrix} 4 & 0 \\ 3 & -5 \end{bmatrix}
\begin{bmatrix} 0.707106 * 0.15812 + 0 & 0 + 0.707106 * 0.31623 \\ -0.707106 * 0.15812 + 0 & 0 + 0.707106 * 0.31623 \end{bmatrix}\\
=\begin{bmatrix} 4 & 0 \\ 3 & -5 \end{bmatrix}
\begin{bmatrix} 0.11181 & 0.2236 \\ -0.11181 & 0.2236 \end{bmatrix}\\
=\begin{bmatrix} 0.44724 & 0.89448 \\ 0.89448 & -0.44724 \end{bmatrix}
よって、ここに$U$、$V$、$\Sigma$が以下のようにそろった。
U=\begin{bmatrix} 0.44724 & 0.89448 \\ 0.89448 & -0.44724 \end{bmatrix}, V = \begin{bmatrix} 0.707106 & 0.707106 \\ -0.707106 & 0.707106 \end{bmatrix}, \Sigma=\begin{bmatrix} 6.32456 & 0 \\ 0 & 3.1623 \end{bmatrix}
最後に分解した$U$、$V$、$\Sigma$を用いて、次式から$A$を求めて検算する。
A_{m×n}=U_{m×r}\Sigma_{r×r} V^{T}_{n×r}
値を代入して、
A
=\begin{bmatrix} 0.44724 & 0.89448 \\ 0.89448 & -0.44724 \end{bmatrix}
\begin{bmatrix} 6.32456 & 0 \\ 0 & 3.1623 \end{bmatrix}
\begin{bmatrix} 0.707106 & -0.707106 \\ 0.707106 & 0.707106 \end{bmatrix}\\
=\begin{bmatrix} 0.44724 & 0.89448 \\ 0.89448 & -0.44724 \end{bmatrix}
\begin{bmatrix} 4.4721 & -4.4721 \\ 2.2361 & 2.2361 \end{bmatrix}
=\begin{bmatrix} 4 & 0 \\ 3 & 5 \end{bmatrix}
元の$A$に戻った!
3. コード
numpyを使うと、$V$は$V^T$として帰ってくるので注意
import numpy as np
A = np.array([
[4, 0],
[3, -5]
])
U, s, V = np.linalg.svd(A, full_matrices=True)
print(U)
print(np.diag(s))
print(V)
print("---")
# a = usv
print( np.dot( U, np.dot(np.diag(s), V)) )
手計算と一致した!