2d-CxNN(Complex-valued Neural Network: 複素ニューラルネットワーク)に入門する① (回帰篇)

0. 概要

CxNN(Complex-valued Neural Network)は、複素ニューラルネットワークを指しCVNNやCxNNといった呼び方がある。
今まで線形的な処理をしていたDNNと比較して、周期性を持つデータや、空間的な拡大、縮小、回転を必要とするデータ等を処理することに強みがある。内部データ的には入力、重みが複素数になっている。

ここで複素ニューラルネットワークの特徴が分かりやすい図を以下に示す。

左がDNN、右がCxNN（参考: https://ssuzumura.github.io/research2012/cvnn.html）

ということで、CxNNがDNNよりも周期性を再現できていることが分かる。
今回はこの図を作成することを目指していく。

1. 理論

複素ニューラルネットワークの実装をするにあたって、複素数の定義、複素ニューラルネットワークの数式の定義を行う。
今回は首記の通り、2次元に限る。

1.1. 複素数の定義

まず複素数を以下のように定義する。

z=x+iy

ここで、各変数は

x=\cos\theta \\
y=\sin\theta

と定義し、虚数成分が$y$の$sin$、実数成分が$x$の$cos$である。

複素数の掛け算は$i^2=-1$という制約の基、$x$と$w$の複素数(実数: $^{re}$、虚数: $^{im}$)が与えられた場合、以下のように定義される。

(x^{re}+x^{im}_{i})(w^{re}+w^{im}_{i}) \\
= x^{re}w^{re} + x^{im}_{i}w^{re}+x^{re}w^{im}_{i}+x^{im}_{i}w^{im}_{i}\\
= x^{re}w^{re} + x^{im}_{i}w^{re}+x^{re}w^{im}_{i}+(-1\cdot(x^{im}w^{im})) \\
= (x^{re}w^{re}-x^{im}w^{im}) + (x^{re}w^{im} + x^{im}w^{re})_{i}

$i^2=-1$といった制約があるおかげで回転を表現できる。$im$同士を掛けることで90度回転する。
すなわち、$im * im * im * im = -1 * -1 = 1$となり、360度の回転をする。

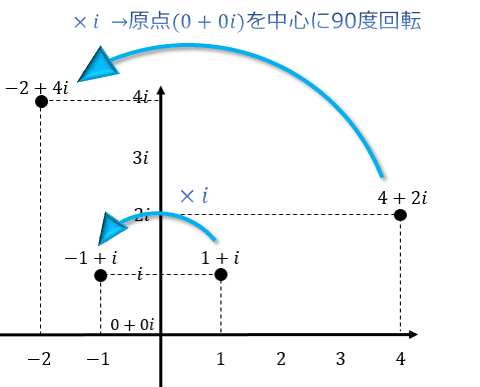
複素数を用いた回転(https://atarimae.biz/archives/500)
このように$im$を掛けるだけで各象限間を遷移することができる。

1.2. 一般的なニューラルネットワーク

一般的なニューラルネットワークの数式を簡易的に整理する。

1.2.1. Forward propagation

ニューラルネットワークのAffineレイヤーにおける演算は以下で行われる。$w$が重みで$x$が入力である。

\widehat {y}=(\sum x \cdot  w ) + b

複素ニューラルネットワークでは、$w$及び$x$が複素数になる。

1.3. CxNNのニューラルネットワーク

複素数の定義からニューラルネットワークを複素数に拡張する。

1.3.1. Forward propagation

入力、重み、出力が全て複素数になる。$real$、$imag$は分けて計算する。
よって重みの計算は以下のように計算できる。ここで、$w$を重み、$b$をバイアス、$x$を入力、$y$を出力とする。

\widehat {y}=(\sum w \cdot  x ) + b=\sum (x^{re}+x^{im})(w^{re}+w^{im}) + b

このため、各実部と虚部は以下のように計算できる。

\widehat {y}^{re} = (\sum x \cdot  w ) + b=\left\{ \sum (x^{re}w^{re}) - \sum (x^{im}w^{im}) \right\} +b^{re} \\
\widehat {y}^{im} = (\sum x \cdot  w ) + b=\left\{ \sum (x^{re}w^{im}) + \sum ( x^{im}w^{re})\right\}+b^{im}

2. 実装

今回は円の波形データを10個与えると、次の位置を推論する複素ニューラルネットワークをKerasにて実装する。

2.1. データの作成

今回は$x^2+y^2=r^2$をCxNNで再現したい。
そこで、第4象限が欠損しているデータを1rad解像度で作る。また、テストデータは欠損前から10rad分のデータを作る。
今回は周期性の獲得を確認したいので、スケール量も変更する。

青色がトレーニングデータ、オレンジ色がテストデータである。

実数と虚数で見るとこんな感じ。

ソースコードは以下である。

  start_rad = 0
  end_rad = 270
  sampling = 270
  scale_num = 5
  scale_rad = 10

  x,y=[],[]

  for i in range(1, scale_num+1):
    for j in np.linspace(start_rad, end_rad, sampling):
        x.append(math.cos(math.radians(j)) * (i * scale_rad) )
        y.append(math.sin(math.radians(j)) * (i * scale_rad) )

  # 10個の連続値データから次のデータを推定
  data_length = 10
  train_data = np.empty((0, 2, data_length))  
  label_data = np.empty((0, 2, 1))
  test_data = np.empty((0, 2, data_length))  

  # 10個の点群
  train_tmp = np.zeros((2, data_length))
  test_tmp = np.zeros((2, data_length))

  # 10個の点群から次の1個を推定
  label_tmp = np.zeros((2, 1))

  # each scale
  for i in range(scale_num):
    # data
    xr = x[sampling*i: (sampling*i) + sampling]
    yi = y[sampling*i: (sampling*i) + sampling]

    # test_data
    test_tmp[0, :] = xr[-data_length:]
    test_tmp[1, :] = yi[-data_length:]
    test_data = np.append(test_data, [test_tmp], axis=0)

    # スケール毎にサンプリングを1つ1つズラしたデータを作成
    for j in range(sampling - (data_length + 1) ):
      #train
      # real
      train_tmp[0, :] = xr[j:(j+data_length)]
      # imag
      train_tmp[1, :] = yi[j:(j+data_length)]

      # label
      # real
      label_tmp[0] = xr[j+data_length]
      # imag
      label_tmp[1] = yi[j+data_length]

      # save
      train_data = np.append(train_data, [train_tmp], axis=0)
      label_data = np.append(label_data, [label_tmp], axis=0)

      #train_data.append(train_tmp)
      #label_data.append(label_tmp)


  ## adding test data ##
  for i in range(4):
    tx, ty = [], []
    # 分解能分のデータを作る
    for j in np.linspace(end_rad - data_length, end_rad,  data_length * int(end_rad/sampling) ):
      tx.append(math.cos(math.radians(j)) * ( (scale_num+1 + i) * scale_rad) )
      ty.append(math.sin(math.radians(j)) * ( (scale_num+1 + i) * scale_rad) )

    test_tmp[0, :] = tx
    test_tmp[1, :] = ty
    test_data = np.append(test_data, [test_tmp], axis=0)

2.2. DNNの作成

今回は複素数のデータが入力として渡されるので、ラムダ式を用い実数、虚数を分割し、
1次元に結合してからWeightを畳み込む。畳み込んだ結果は、また実数及び虚数に分解してから返す。

class G2DAffine(Layer):
  def __init__(self, output_dim, activation, **kwargs):
    self.output_dim = output_dim
    self.activation = activation
    super(G2DAffine, self).__init__(**kwargs)

  def build(self, input_shape):

    # input shape: [batchNum][Real/Imag][Data]
    # Initialize
    self.weight = self.add_weight(name='weight_real',
                                  shape=(input_shape[2]*2, self.output_dim*2),
                                  initializer='glorot_uniform')

    super(G2DAffine, self).build(input_shape)

  def call(self, x):
    # input shape: [batchNum][Real/Imag][Data]
    x_real = Lambda(lambda x: x[:, 0, :], output_shape=(x.shape[2], ))(x) # real
    x_imag = Lambda(lambda x: x[:, 1, :], output_shape=(x.shape[2], ))(x) # imag

    if self.activation == 'identify':
      # Calc: [batchNum][Output]
      cmpx = keras.layers.concatenate([x_real, x_imag], axis=1)
      cmpx = K.dot(cmpx, self.weight)
      real = Lambda(lambda x: x[:, 0:self.output_dim])(cmpx) # real
      imag = Lambda(lambda x: x[:, self.output_dim:])(cmpx) # imag
      # Expand: [batchNum][1][Output]
      real = K.expand_dims(real, 1)
      imag = K.expand_dims(imag, 1)
      # Merge: [batchNum][2][Output]
      cmpx = keras.layers.concatenate([real, imag], axis=1)
      return cmpx

  def compute_output_shape(self, input_shape):
    #  (input_shape[0], self.output_dim)
    # Unpack tuple (BatchNum, (2, DataNum)) -> (BatchNum, 2, DataNum) 
    return(input_shape[0], 2, self.output_dim)

ここでは未だ複素数の演算を行っていない。

2.3. CxNNの作成

理論で説明したように渡されてきた複素数を実数、虚数に分解してから計算を行う。

class Cx2DAffine(Layer):
  def __init__(self, output_dim, activation, **kwargs):
    self.output_dim = output_dim
    self.activation = activation
    super(Cx2DAffine, self).__init__(**kwargs)

  def build(self, input_shape):
    # input shape: [batchNum][Real/Imag][Data]
    # Initialize
    self.weight_real = self.add_weight(name='weight_real',
                                  shape=(input_shape[2], self.output_dim),
                                  initializer='glorot_uniform')

    self.weight_imag = self.add_weight(name='weight_imag',
                                  shape=(input_shape[2], self.output_dim),
                                  initializer='glorot_uniform')

    self.bias_real   = self.add_weight(name='bias_real',
                                  shape=(1, self.output_dim),
                                  initializer='zeros')

    self.bias_imag   = self.add_weight(name='bias_imag',
                                  shape=(1, self.output_dim),
                                  initializer='zeros')

    super(Cx2DAffine, self).build(input_shape)

  def call(self, x):
    # input shape: [batchNum][Real/Imag][Data]
    x_real = Lambda(lambda x: x[:, 0, :], output_shape=(x.shape[2], ))(x) # real
    x_imag = Lambda(lambda x: x[:, 1, :], output_shape=(x.shape[2], ))(x) # imag

    if self.activation == 'identify':
      # Calc: [batchNum][Output]
      real = K.dot(x_real, self.weight_real) - K.dot(x_imag, self.weight_imag) 
      imag = K.dot(x_real, self.weight_imag) + K.dot(x_imag, self.weight_real) 

      real = real + self.bias_real
      imag = imag + self.bias_imag

      # Expand: [batchNum][1][Output]
      real = K.expand_dims(real, 1)
      imag = K.expand_dims(imag, 1)

      # Merge: [batchNum][2][Output]
      cmpx = keras.layers.concatenate([real, imag], axis=1)
      return cmpx

  def compute_output_shape(self, input_shape):
    #  (input_shape[0], self.output_dim)
    # Unpack tuple (BatchNum, (2, DataNum)) -> (BatchNum, 2, DataNum) 
    return(input_shape[0], 2, self.output_dim)

なお、モデルは以下である。

  # input shape: [batchNum][Real/Imag][Data]
  input = Input(shape=(2, data_length,))
  cxnn = Cx2DAffine(128, activation='identify')(input)
  cxnn = Cx2DAffine(128, activation='identify')(cxnn)
  cxnn = Cx2DAffine(128, activation='identify')(cxnn)
  cxnn = Cx2DAffine(1, activation='identify')(cxnn)
  regression = Model(input, cxnn)
  regression.compile(optimizer='adam', loss=loss_function)
  print(regression.summary())
  regression.fit(train_data, label_data, epochs=10, batch_size=10, shuffle=True)

2.3. Lossの作成

特に作らずとも、Kerasが上手いことやってくれるが、検証用に作成しておく。
実数と虚数に分けて損失を計算する。

def loss_function(y_hat, y):
    y_hat_real = Lambda(lambda x: x[:, 0, 0])(y_hat) # real
    y_hat_imag = Lambda(lambda x: x[:, 1, 0])(y_hat) # imag

    y_real = Lambda(lambda x: x[:, 0, 0])(y) # real
    y_imag = Lambda(lambda x: x[:, 1, 0])(y) # imag

    real_loss = K.mean(K.abs(y_hat_real - y_real))
    imag_loss = K.mean(K.abs(y_hat_imag - y_imag))

    return  real_loss + imag_loss

2.4. テスト

10個前のデータを読み込んで、1つ先を予測するプログラムである。10個先まで予測すれば、入力データに真値は一切なくなる。
このため、周期性を獲得出来ているか確認するため、100度先まで推定させてみる。

  td = deepcopy(test_data)
  for i in range(100):
    ret = regression.predict(td[:, :, -data_length:])
    td = np.append(td, ret, axis=2)

3. 結果

いくつかの推論結果を示す。

ケース1

CxNNの結果は以下である。学習していないスケールのテストデータを復元しているので、周期性の獲得が出来ているといえる。

さて、DNNはどんなものか・・・と気になるところ。

なんだ、お前ってやつは優秀だな。

ニューロンの数を減らしたり、教師データの量を減らしたり色々と調整をすると確かに複素ニューラルネットワークの方が精度が高い時がある。しかし、死ぬほどDenseをスタックできる時代、どちらを使ってもあまり変わらない・・・。汎化性能はもはやDNNの方が上な気がする。

ケース2

こんな感じのデータを作成する。

  end_rad = 270
  sampling = 270
  scale_num = 5
  scale_rad = 10
  data_length = 10
  x,y=[],[]
  # define time and space domains
  pi = 3.1415926535897923846
  x = np.linspace(0.1, 0.2, scale_num) # space
  t = np.linspace(0, 6*pi, sampling) # time
  dt = t[2] - t[1]
  Xm,Tm = np.meshgrid(x, t) # sapce & time
  f = np.multiply(5*np.multiply(1/np.cosh(Xm/2), np.tanh(Xm/2)), 2*np.exp((0.1+2.8j)*Tm))

データと未学習データ

CxNNの結果

DNNの結果

やばい、DNNさん優秀か・・・

ケース3

今までは出力が1つであったが、次は出力（オレンジ色）が10個である。
また今までは10個のデータを読み込んで、1つの出力であったが、今回は10個のデータ(スケール離れている)を読み込んで10個のデータを出力する。このため、より高精度な識別機が求められる。

データは以下である。

まずは、CxNNさん。芸術点は高いといったところか

そして、DNNさん。多少の誤差はあるものの正しい

圧倒的敗北

実装が間違っている？CxNNは最急降下法が使えないみたいだ。しかし、トレーニング中のロスは$e-12$とかだぞ・・・。

ケース3のその後、、、

活性化関数を工夫してみたところ、CxNNでも近似できることがわかった。

しかし、135度分の回転をさせているのに、300度くらい回っちゃってる。