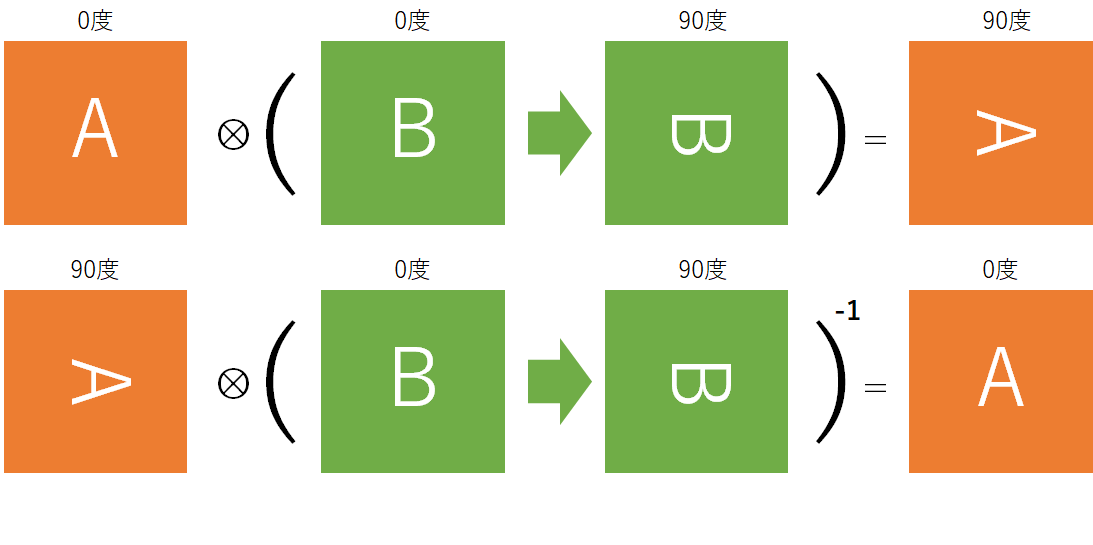
0. 概要
姿勢を推定しようとしたところ、意外に困ったことが多かったので足回りの数式をまとめてみた。
特に、一般的な変換順序の回転行列は検索すれば出てくるのだけれども、いざ自身の開発しているプログラムに取り込もうとするとオーダーが異なっていて上手く取り込めないという事態が多く、ゼロベースから計算しているウェブサイトも余り見当たらなかったので、その辺について重点的に触れている。
1.0 姿勢について
まず、ある物体の姿勢を表す時に用いる代表的な数式とその長短について説明する。
1.1 ロール・ピッチ・ヨー/オイラー角 (Euler angles)
ロール・ピッチ・ヨー
一番、シンプルな方法として直交する3軸毎に回転角を設定するロール・ピッチ・ヨーの表現がある。
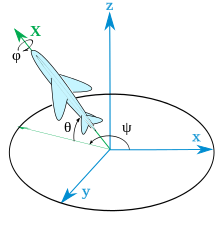
例えば、直交した3軸を次の順番Z->Y->Xで回転させた場合以下のようになる。

http://www.mech.tohoku-gakuin.ac.jp/rde/contents/course/robotics/coordtrans.html
この手法の重要なところは、最初にZ軸周りに回転するとX, Yも追従して回転が保存される。
この保存された回転を基にY->Xと軸周りに回転を加えていくので、あらゆる角度(姿勢)を表現することができる。
オイラー角
なお、この表現系は3軸を使わなくても2軸でも表現できる。
例えば、以下の手順で回転を試みる。
$(x, y, z)$をz軸まわりに$a$度回転させ$(x', y', z')$とする
$(x', y', z')$をx軸まわりに$β$度回転させ$(x'', y'', z'')$とする
$(x'', y'', z'')$をz軸まわりに$γ$度回転させ$(X, Y, Z)$とする
この時、$(α, β, γ)$をオイラー角といい、$(X, Y, Z)$はあらゆる姿勢を表現できる。
しかし、ある姿勢角の時ジンバルロックという自由度が減ってしまう現象が起こる。
下記の図の場合、Z軸とY軸が重なってしまった時に起こる。
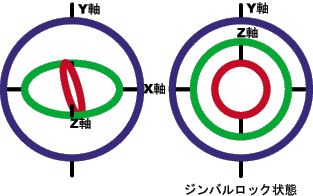
ジンバルロックは2番目に回す軸周りの角度が±90度の時に発生する
ロール・ピッチ・ヨーとオイラー角の違いは、
ロール・ピッチ・ヨーは$(x, y, z)$の3軸に回転を行っていたのに対して、
オイラー角の場合は$(x, z)$の2軸に対してしか回転をしていない。
どちらも回転処理を行ったのは3回であるが、何の軸を取るかによってその名称が変わるということである。
といっても、厳密にロール・ピッチ・ヨーとオイラー角の違いは決まっていない。
$(x, y, z)$の軸に対して$(α, β, γ)$のオイラー角分、回転させるという動作は同じである。
換可則性
なお、これら2つの方法について換可則性はない。
よって、Z->Y->XやX->Y->Zの順で軸まわりに回転させると、異なった姿勢が得られる。
これらの組み合わせは3軸回転と2軸回転で合わせて12通りある。
| x-y-z | x-z-y | y-x-z | y-z-x | z-x-y | z-y-x |
| x-y-x | x-z-x | y-x-y | y-z-y | z-x-z | z-y-z |
これらはz-x-z系や3-1-3系等と呼ばれたりしている。
回転行列を求める
$(x, y, z)$軸に対応するオイラー角が$(α, β, γ)$の時、x -> y -> zの順に回転を加える回転行列を計算する。
まず各軸まわりの回転行列を求める。
{\bf R_x}=\left(\begin{array}{ccc}1 &0 &0 \\0&\cos \alpha&\sin \alpha\\0 &-\sin \alpha &\cos\alpha \\\end{array}\right)\\
{\bf R_y}=\left(\begin{array}{ccc}\cos \beta &0 & \sin \beta\\ 0& 1 &0\\-\sin \beta & 0 &\cos\beta \\\end{array}\right)\\
{\bf R_z}=\left(\begin{array}{ccc} \cos \gamma&\sin \gamma&0\\ -\sin \gamma &\cos\gamma&0 \\ 0&0 &1 \\ \end{array}\right)
次に回転順通りに行列式を計算して、最終的な回転行列を得る。
\left(\begin{array}{c}\vec{\mathbf e}_X\\ \vec{\mathbf e}_Y \\ \vec{\mathbf e}_Z\end{array}\right)={\bf R_xR_yR_z}\left(\begin{array}{c}\vec{\mathbf e}_x\\ \vec{\mathbf e}_y \\ \vec{\mathbf e}_z\end{array}\right)
\left(\begin{array}{c}\vec{\mathbf e}_X\\ \vec{\mathbf e}_Y \\ \vec{\mathbf e}_Z\end{array}\right)={
\begin{equation}
\left(
\begin{array}{ccc}
\cos \beta \cos \gamma & -\cos \beta \sin \gamma & \sin \beta \\
\cos \beta \sin \gamma + \cos \gamma \sin \alpha \sin \beta &
\cos \alpha \cos \gamma - \sin \alpha \sin \beta \sin \gamma &
-\cos \beta \sin \alpha \\
\sin \alpha \sin \gamma - \cos \alpha \cos \gamma \sin \beta &
\cos \gamma \sin \alpha + \cos \alpha \sin \beta \sin \gamma &
\cos \alpha \cos\beta \\
\end{array}
\right)
\end{equation}
}\left(\begin{array}{c}\vec{\mathbf e}_x\\ \vec{\mathbf e}_y \\ \vec{\mathbf e}_z\end{array}\right)
1.2 クォータニオン (Quaternion)
クォータニオンとは四元数ともいい、4つのパラメータ$q = (x, y, z, w)$から姿勢を表す。
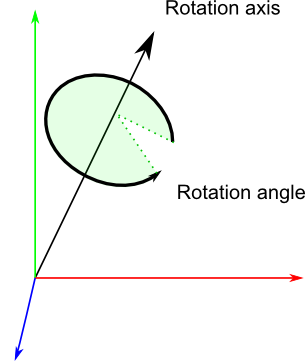
$x, y, z$がRotation axis、すなわち回転軸を表す。$w$が回転軸まわりの回転(Rotation angle)を表す。
各変数は結束性があり、正規化されるため$x^2 + y^2 + z^2 + w^2=1$である。
複素数クォータニオン
計算を簡単化するため、四元数を複素数として扱って説明していく。
まずは、四元数の複素数を以下のように定義する。
q=w+ix+jy+kz
ここで、$w$は実数とし、添え字$i, j, k$は虚数のような性質を持ち、可換測は成り立たないものとする。
よって、$w$を実部、$i, j, k$を虚部とする。
単位乗積表は以下である。
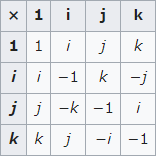
例えば、$-k=ijkk=ij(k^2)=ij(-1)$のため$k=ij$を導ける。
これらをまとめると、以下の積の法則が得られる
i^2=j^2=k^2=ijk=-1\\
ij=k\\
jk=i\\
ki=j\\
ji=-k\\
kj=-i\\
ik=-j
※左側因子を列、右側因子を行とする
複素数クォータニオンの掛け算
次に、$w_{a}+x_{a}+y_{a}+z_{a}$と$w_{b}+x_{b}+y_{b}+z_{b}$の2つの四元数の積を以下のように定義する
(w_{a}+x_{a}+y_{a}+z_{a})(w_{b}+x_{b}+y_{b}+z_{b})
これら2つをハミルトン積として解く。解は基底間の積と分配律によって与えられる。
従って、
(w_{a}+x_{a}^{i}+y_{a}^{j}+z_{a}^{k})(w_{b}+x_{b}^{i}+y_{b}^{j}+z_{b}^{k}) \\
=w_{a}w_{b}+w_{a}x_{b}^{i}+w_{a}y_{b}^{j}+w_{a}z_{b}^{k}\\
+x_{a}^{i}w_{b}+x_{a}^{i}x_{b}^{i}+x_{a}^{i}y_{b}^{j}+x_{a}^{i}z_{b}^{k}\\
+y_{a}^{j}w_{b}+y_{a}^{j}x_{b}^{i}+y_{a}^{j}y_{b}^{j}+y_{a}^{j}z_{b}^{k}\\
+z_{a}^{k}w_{b}+z_{a}^{k}x_{b}^{i}+z_{a}^{k}y_{b}^{j}+z_{a}^{k}z_{b}^{k}
となり、単位乗積表から各変数を置き換える。
例えば、$y_{a}^{j}x_{b}^{i}$の場合は$ji$なので単位乗積表から$-k$に置き換えられるため、$-(y_{a}x_{b})_{k}$となる。
これらを置き換え、展開し整理すると以下になる。
(w_{a}+x_{a}^{i}+y_{a}^{j}+z_{a}^{k})(w_{b}+x_{b}^{i}+y_{b}^{j}+z_{b}^{k})\\
=(w_{a}w_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b})\\
+(w_{a}x_{b}+x_{a}w_{b}+y_{a}z_{b}-z_{a}y_{b})_i\\
+(w_{a}y_{b}+y_{a}w_{b}+z_{a}x_{b}-x_{a}z_{b})_j\\
+(w_{a}z_{b}+z_{a}w_{b}+x_{a}y_{b}-y_{a}x_{b})_k
各次元で表記すると以下のようになる。
w^{re} = (w_{a}w_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b})
\\x^{i} = (w_{a}x_{b}+x_{a}w_{b}+y_{a}z_{b}-z_{a}y_{b})
\\y^{j} = (w_{a}y_{b}+y_{a}w_{b}+z_{a}x_{b}-x_{a}z_{b})
\\z^{k} = (w_{a}z_{b}+z_{a}w_{b}+x_{a}y_{b}-y_{a}x_{b})
行列式にするとこのようにも表記可能である。
{Q = xw =
\begin{pmatrix}
x_w & -x_z & x_y & x_x \\
x_z & x_w & -x_x & x_y \\
-x_y & x_x & x_w & x_z \\
-x_x & -x_y & -x_z & x_w
\end{pmatrix}
\begin{pmatrix}
w_x \\
w_y \\
w_z \\
w_w
\end{pmatrix}
}
例えば、$q_1$が$y$軸まわりに90度回転したクォータニオンで、$q_2$が$x$軸まわりに90度回転したクォータニオンだった時、この二つを掛け合わせると、単純に$y$軸、$x$軸が90度回転した姿勢が得られる。
複素数クォータニオンのインバース
共役四元数すなわち$Q^{-1}$は以下である。
\overline{Q} = w-x^{i}-y^{j}-z^{k} \\
Q\overline{Q}= \overline{Q}Q = w^{2}+x^{2}+y^{2}+z^{2}\\
Q\overline{Q}= \overline{Q}Q = (1, 0, 0, 0)
虚数の性質をもつ関係性から定式が成り立つのは容易に理解できる。
全く同じクォータニオン同士の$QQ^{-1}$は$w=1$以外が0になる。
複素数クォータニオンの長さ
なお、絶対値の求め方は三平方の定理から容易に求められる。
\left| Q\right| =\sqrt {Q\overline {Q}}=\sqrt {w^{2}+x^{2}+y^{2}+z^{2}}
$\left| Q\right|=1$である。なお、$\left| Q\right| = 0$は各要素$w=x=y=z=0$の時だけである。
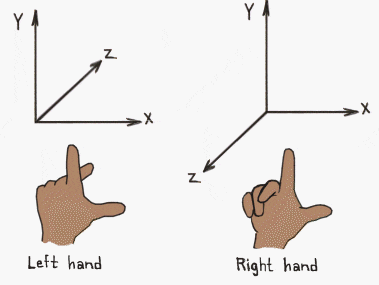
クォータニオン→クォータニオンの回転行列(右手座標系、左手座標系)
右手座標系の話
クォータニオンの回転行列を求める。
世の中一般的に右手座標系が多く用いられているため、この回転行列も右手座標系のものである。
右手から左手への変換は非常に簡単なので末尾で触れる。
では、クォータニオンの回転行列を求めていく。
まず、クォータニオンの積は以下で表現される。
(w_{a}+x_{a}^{i}+y_{a}^{j}+z_{a}^{k})(w_{b}+x_{b}^{i}+y_{b}^{j}+z_{b}^{k})\\
=(w_{a}w_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b})\\
+(w_{a}x_{b}+x_{a}w_{b}+y_{a}z_{b}-z_{a}y_{b})_i\\
+(w_{a}y_{b}+y_{a}w_{b}+z_{a}x_{b}-x_{a}z_{b})_j\\
+(w_{a}z_{b}+z_{a}w_{b}+x_{a}y_{b}-y_{a}x_{b})_k
これを分解し、$q_1 \otimes q_2 = q_2 L_{row}(q_1)$のように変形する。
\begin{pmatrix}
w_{a}x_{b} & x_{a}w_{b} & y_{a}z_{b} & -z_{a}y_{b}\\
w_{a}y_{b} & y_{a}w_{b} & z_{a}x_{b} & -x_{a}z_{b}\\
w_{a}z_{b} & z_{a}w_{b} & x_{a}y_{b} & -y_{a}x_{b}\\
w_{a}w_{b} & -x_{a}x_{b} & -y_{a}y_{b} & -z_{a}z_{b}
\end{pmatrix}
=
\begin{pmatrix}
x_b & y_b & z_b & w_b
\end{pmatrix}
\begin{pmatrix}
w_a & z_a & -y_a & -x_a\\
-z_a & w_a & x_a & -y_a\\
y_a & -x_a & w_a & -z_a\\
x_a & y_a & z_a & w_a
\end{pmatrix}
次に、これを入れ替えた$q_1 \otimes q_2 = q_1 R_{row}(q_2)$も計算する。
\begin{pmatrix}
w_{a}x_{b} & x_{a}w_{b} & y_{a}z_{b} & -z_{a}y_{b}\\
w_{a}y_{b} & y_{a}w_{b} & z_{a}x_{b} & -x_{a}z_{b}\\
w_{a}z_{b} & z_{a}w_{b} & x_{a}y_{b} & -y_{a}x_{b}\\
w_{a}w_{b} & -x_{a}x_{b} & -y_{a}y_{b} & -z_{a}z_{b}
\end{pmatrix}
=
\begin{pmatrix}
x_a & y_a & z_a & w_a
\end{pmatrix}
\begin{pmatrix}
w_b & -z_b & y_b & -x_b\\
z_b & w_b & -x_b & -y_b\\
-y_b & x_b & w_b & -z_b\\
x_b & y_b & z_b & w_b
\end{pmatrix}
ここで得られたこの2つを使って、回転行列を計算する。
L_{row}(q_1)=\begin{pmatrix}
w_a & z_a & -y_a & -x_a\\
-z_a & w_a & x_a & -y_a\\
y_a & -x_a & w_a & -z_a\\
x_a & y_a & z_a & w_a
\end{pmatrix}
R_{row}(q_2)=\begin{pmatrix}
w_b & -z_b & y_b & -x_b\\
z_b & w_b & -x_b & -y_b\\
-y_b & x_b & w_b & -z_b\\
x_b & y_b & z_b & w_b
\end{pmatrix}
この$R_{row}(q2)$成分に対して共役$q^{-1}$($w$以外を反転)を計算する。そうすると以下のようになる。
L_{row}(q)=\begin{pmatrix}
w & z & -y & -x\\
-z & w & x & -y\\
y &-x & w & -z\\
x & y & z & w
\end{pmatrix}
R_{row}(q^{-1})=\begin{pmatrix}
w & z & -y & x\\
-z & w & x & y\\
y & -x & w & z\\
-x & -y & -z & w
\end{pmatrix}
これで全ての道具が揃ったので、$Q_{row}=R_{row}(q^{-1}) \cdot L_{row}(q)$を計算してクォータニオンの回転行列を得る。
Q_{row}=R_{row}(q^{-1}) \cdot L_{row}(q)
\\
=
\begin{pmatrix}
w & z & -y & x\\
-z & w & x & y\\
y & -x & w & z\\
-x & -y & -z & w
\end{pmatrix}
\cdot
L_{row}(q)=\begin{pmatrix}
w & z & -y & -x\\
-z & w & x & -y\\
y &-x & w & -z\\
x & y & z & w
\end{pmatrix}
\\
=
\begin{pmatrix}
-{{z}^{2}}-{{y}^{2}}+{{x}^{2}}+{{w}^{2}} & 2 w z+2 x y & 2 x z-2 w y & 0\\
2 x y-2 w z & -{{z}^{2}}+{{y}^{2}}-{{x}^{2}}+{{w}^{2}} & 2 y z+2 w x & 0\\
2 x z+2 w y & 2 y z-2 w x & {{z}^{2}}-{{y}^{2}}-{{x}^{2}}+{{w}^{2}} & 0\\
0 & 0 & 0 & {{z}^{2}}+{{y}^{2}}+{{x}^{2}}+{{w}^{2}}\end{pmatrix}
この時、$w^2+x^2+y^2+z^2=1$の性質を使うことで、以下のよう整理できる。
Q_{row}=R_{row}(q^{-1}) \cdot L_{row}(q)=
\begin{pmatrix}
1-2y^2-2z^2 & 2 w z+2 x y & 2 x z-2 w y & 0\\
2 x y-2 w z & 1-2x^2-2z^2 & 2 y z+2 w x & 0\\
2 x z+2 w y & 2 y z-2 w x & 1-2x^2-2y^2& 0\\
0 & 0 & 0 & 1
\end{pmatrix}
左手座標系の話
そして、最後に左手座標系であるが、こちらは$q^{-1}$してから計算するだけで簡単に求まる。
また、$q^{T}$でも良い。
よって、上記で求めた$Q_{row}^{T}$を計算すると以下のようにUnity等で用いられる左手座標系のクォータニオンの回転行列が得られる。
Q_{row}^{T}=Q_{left}=
\begin{pmatrix}-{{z}^{2}}-{{y}^{2}}+{{x}^{2}}+{{w}^{2}} & 2 x y-2 w z & 2 x z+2 w y & 0\\
2 w z+2 x y & -{{z}^{2}}+{{y}^{2}}-{{x}^{2}}+{{w}^{2}} & 2 y z-2 w x & 0\\
2 x z-2 w y & 2 y z+2 w x & {{z}^{2}}-{{y}^{2}}-{{x}^{2}}+{{w}^{2}} & 0\\
0 & 0 & 0 & {{z}^{2}}+{{y}^{2}}+{{x}^{2}}+{{w}^{2}}\end{pmatrix}
最後に、この計算を求めたMaximaのソースコードを示す。
r: matrix([w, -z, y, -x], [z, w, -x, -y], [-y, x, w, -z], [x, y, z, w]);
l: matrix([w, -z, y, x], [z, w, -x, y], [-y, x, w, z], [-x, -y, -z, w]);
rl: r.l;
transpose(rl);
クォータニオン→任意軸回転行列 (ロドリゲス)
クォータニオンの各要素を回転軸ベクトル$n$と回転角度$\theta$を用いて表すと以下のようになる。
q_x = n_x \cdot \sin \dfrac{\theta}{2} \\
q_y = n_y \cdot \sin \dfrac{\theta}{2} \\
q_z = n_z \cdot \sin \dfrac{\theta}{2} \\
q_w = \cos \dfrac{\theta}{2} \\
n_x = 2q \csc \cdot \theta, \sin(\theta) \neq 0 \\
これを任意軸回転行列としてクォータニオンで表すと以下になる。
{\bf R} = {\begin{pmatrix}
1-2q_y^2-2q_z^2 & 2q_xq_y+2q_wq_z & 2q_xq_z-2q_wq_y & 0\\
2q_xq_y-2q_wq_z & 1-2q_x^2-2q_z^2 & 2q_yq_z+2q_wq_x & 0 \\
2q_xq_z+2q_wq_y & 2q_yq_z-2q_wq_x & 1-2q_x^2-2q_y^2 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
}
クォータニオンの値を実際に代入して式を展開していけば以下の任意軸回転行列の数式(ロドリゲスの回転公式)と一致するはずである。
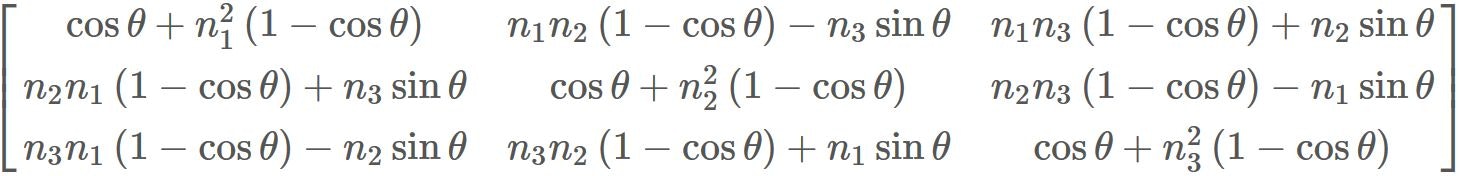
本当に一致するのか計算してみる。
まず任意軸回転行列の左上$m_{00}$に着目する。
1-2q_y^2-2q_z^2
これを最終的にロドリゲスの回転行列$m_{00}$と一致させる。
\cos \theta + n^2_x(1-\cos \theta)
すなわち、以下のようになるはずである。
1-2q_y^2-2q_z^2 = \cos \theta + n^2_x(1-\cos \theta)
まず、$1-2q_y^2-2q_z^2$の$-2q_y^2$を展開する。
-2q_y^2 = -2 \cdot (n_y \cdot \sin \dfrac{\theta}{2}) * (n_y \cdot \sin \dfrac{\theta}{2}) \\
= -2 \cdot n_y^2 \cdot \sin^2(\dfrac{\theta}{2})
※$q_x = n_y \cdot \sin \dfrac{\theta}{2}$
ここで、2乗成分が出てきており倍角の公式が当てはまることが分かる。
倍角の公式$\cos2(\theta) = \cos^2\theta - \sin^2\theta = 1 - 2\sin^2\theta$を展開し$\cos(\theta) = 1 - 2\sin^2(\frac{\theta}{2})$を用いる。
展開は以下のように行い、
\cos2(\theta) = \cos^2\theta - \sin^2\theta = 1 - 2\sin^2\theta\\
\cos(\theta) = 1 - 2\sin^2(\frac{\theta}{2})\\
\cos(\theta) - 1 = - 2\sin^2(\frac{\theta}{2})\\
これを用い、$-2 \cdot n_y^2 \cdot \sin^2(\dfrac{\theta}{2})$を整理すると以下になる。
n^2_y \cdot - 2\sin^2(\frac{\theta}{2}) = n^2_y \cdot (\cos \theta - 1)
次に、$1-2q_y^2-2q_z^2$の$-2q_z^2$を展開する。三角関数は変わらず$n_y$が$n_z$に代わっただけなので、以下のように置き換える。
n^2_z \cdot - 2\sin^2(\frac{\theta}{2}) = n^2_z \cdot (\cos \theta - 1)
よって、$1-2q_y^2-2q_z^2$は以下のように展開できた。
-2q_y^2= n^2_y \cdot (\cos \theta - 1) \\
-2q_z^2= n^2_z \cdot (\cos \theta - 1)
すなわち、$1 - n^2_y \cdot (\cos \theta - 1) + n^2_z \cdot (\cos \theta - 1)$である。
ここで、忘れてはいけないのが$n$は正規化された値を示しているので、以下の制約がある。
n_x^2 + n_y^2 + n_z^2 = 1
これを$n_z$周りに整理すると、
n_z^2 = 1 - + n_x^2 + n_y^2
となる。これを上記で求めた式に代入する。
1 + (n_y^2(cos \theta - 1)) + ((1 - n_x^2 - n_y^2)(cos \theta - 1)) \\
= 1 + (1 - n_x^2 - n_y^2 + n_y^2)(cos \theta - 1) \\
= 1 + (1 - n_x^2)(cos \theta - 1)
最後にこれを展開して整理すると以下のようになる。
1 + (\cos\theta - 1 - n_x^2cos\theta + n_x^2) \\
=1 + (n_x^2(1 - cos \theta) + cos \theta - 1) \\
= \cos \theta + n_x^2(1 - cos \theta)
これにより、最終的にロドリゲスの回転行列$m_{00}$と一致した。
クォータニオン→任意軸回転行列→方向単位ベクトル
回転状態$q$において、その物体がどちらを向いているのかを得たいと考える。
言い換えると、クォータニオンから任意方向(任意基軸)の単位ベクトルを得る方法を考える。
計算自体は非常に単純で任意軸回転行列から任意軸方向の向きベクトルを掛けてあげればよい。
よって、以下のように定義できる。
$n_{direction} = \bf R \cdot \bf v$
具体的な計算は以下のように行う。
まず、${\bf v} = (x, y, z) = (0, 0, 1)$として$z$を基軸方向と考え、$z$方向の向きベクトルを抽出したいとする。
ここでクォータニオンは4行4列のため、基軸ベクトルの空いた箇所は零空間で埋める。
よって、以下のような計算式が出来る。
{\bf n_{forward-around-z}}={\bf R} \cdot {\bf v_z} = {\begin{pmatrix}
1-2q_y^2-2q_z^2 & 2q_xq_y+2q_wq_z & 2q_xq_z-2q_wq_y & 0\\
2q_xq_y-2q_wq_z & 1-2q_x^2-2q_z^2 & 2q_yq_z+2q_wq_x & 0 \\
2q_xq_z+2q_wq_y & 2q_yq_z-2q_wq_x & 1-2q_x^2-2q_y^2 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
}
{\begin{pmatrix}
0 \\
0 \\
1 \\
0
\end{pmatrix}
}={\begin{pmatrix}
2q_xq_z-2q_wq_y \cdot 1 \\
2q_yq_z+2q_wq_x \cdot 1 \\
1-2q_x^2-2q_y^2 \cdot 1 \\
0
\end{pmatrix}
}
すなわち、$z$軸を基軸として見た方向単位ベクトルは以下で得られる。
{\bf n_{forward-around-z}}=
{\begin{pmatrix}
n_x \\
n_y \\
n_z
\end{pmatrix}
}
={\begin{pmatrix}
2q_xq_z-2q_wq_y \cdot 1 \\
2q_yq_z+2q_wq_x \cdot 1 \\
1-2q_x^2-2q_y^2 \cdot 1
\end{pmatrix}
}
$y$基軸の場合
{\bf n_{forward-around-y}}=
{\begin{pmatrix}
n_x \\
n_y \\
n_z
\end{pmatrix}
}
={\begin{pmatrix}
2q_xq_y+2q_wq_z \cdot 1 \\
1-2q_x^2-2q_z^2 \cdot 1 \\
2q_yq_z-2q_wq_x \cdot 1
\end{pmatrix}
}
$x$基軸の場合
{\bf n_{forward-around-x}}=
{\begin{pmatrix}
n_x \\
n_y \\
n_z
\end{pmatrix}
}
={\begin{pmatrix}
1-2q_y^2-2q_z^2 \cdot 1 \\
2q_xq_y-2q_wq_z \cdot 1 \\
2q_xq_z+2q_wq_y \cdot 1
\end{pmatrix}
}
なお、Unityのコードが基軸周りの方向単位ベクトルを計算するのに参考になる。
public static Vector3 operator *(Quaternion rotation, Vector3 point)
{
float num1 = rotation.x * 2f;
float num2 = rotation.y * 2f;
float num3 = rotation.z * 2f;
float num4 = rotation.x * num1;
float num5 = rotation.y * num2;
float num6 = rotation.z * num3;
float num7 = rotation.x * num2;
float num8 = rotation.x * num3;
float num9 = rotation.y * num3;
float num10 = rotation.w * num1;
float num11 = rotation.w * num2;
float num12 = rotation.w * num3;
Vector3 vector3;
vector3.x = (float) ((1.0 - ((double) num5 + (double) num6)) * (double) point.x + ((double) num7 - (double) num12) * (double) point.y + ((double) num8 + (double) num11) * (double) point.z);
vector3.y = (float) (((double) num7 + (double) num12) * (double) point.x + (1.0 - ((double) num4 + (double) num6)) * (double) point.y + ((double) num9 - (double) num10) * (double) point.z);
vector3.z = (float) (((double) num8 - (double) num11) * (double) point.x + ((double) num9 + (double) num10) * (double) point.y + (1.0 - ((double) num4 + (double) num5)) * (double) point.z);
return vector3;
}
上記の式とプログラムは一致するはずである。
Euler Angles to Quaternion
オイラー角からクォータニオンへの変換を考える。
まずオイラー角は様々な系を取る。例えば、Unityの場合はZ->X->Y系である。
この系の取り方によってクォータニオンの導出の仕方が変わる。
まず、各軸に対してオイラー角(ピッチ・ヨー・ロール)からクォータニオンへの変換式を示す。
ここで$(\phi, \theta, \psi)$をロール・ピッチ、ヨーとする。
{\bf R_x }=
{\begin{bmatrix}
q_w \\
q_x \\
q_y \\
q_z
\end{bmatrix}
}
={\begin{bmatrix}
\cos(\dfrac{\phi}{2})\\
\sin(\dfrac{\phi}{2}) \\
0 \\
0
\end{bmatrix}
}
{\bf R_y }=
{\begin{bmatrix}
q_w \\
q_x \\
q_y \\
q_z
\end{bmatrix}
}
={\begin{bmatrix}
\cos(\dfrac{\theta}{2})\\
0 \\
\sin(\dfrac{\theta}{2}) \\
0
\end{bmatrix}
}
{\bf R_z }=
{\begin{bmatrix}
q_w \\
q_x \\
q_y \\
q_z
\end{bmatrix}
}
={\begin{bmatrix}
\cos(\dfrac{\psi}{2})\\
0 \\
0 \\
\sin(\dfrac{\psi}{2})
\end{bmatrix}
}
この定義の基、X->Y->Z系を計算すると以下のようになる。
{\bf R_{xyz} }= R_{z} \otimes R_{y} \otimes R_{x}\\
={\begin{bmatrix}
\cos(\dfrac{\psi}{2})\\
0 \\
0 \\
\sin(\dfrac{\psi}{2})
\end{bmatrix}
}
{\begin{bmatrix}
\cos(\dfrac{\theta}{2})\\
0 \\
\sin(\dfrac{\theta}{2}) \\
0
\end{bmatrix}
}
{\begin{bmatrix}
\cos(\dfrac{\phi}{2})\\
\sin(\dfrac{\phi}{2}) \\
0 \\
0
\end{bmatrix}
}
=\begin{pmatrix}\sin{\left( \frac{\Theta }{2}\right) } \sin{\left( \frac{\Phi }{2}\right) } \sin{\left( \frac{\Psi }{2}\right) }+\cos{\left( \frac{\Theta }{2}\right) } \cos{\left( \frac{\Phi }{2}\right) } \cos{\left( \frac{\Psi }{2}\right) }\\
\cos{\left( \frac{\Theta }{2}\right) } \sin{\left( \frac{\Phi }{2}\right) } \cos{\left( \frac{\Psi }{2}\right) }-\sin{\left( \frac{\Theta }{2}\right) } \cos{\left( \frac{\Phi }{2}\right) } \sin{\left( \frac{\Psi }{2}\right) }\\
\cos{\left( \frac{\Theta }{2}\right) } \sin{\left( \frac{\Phi }{2}\right) } \sin{\left( \frac{\Psi }{2}\right) }+\sin{\left( \frac{\Theta }{2}\right) } \cos{\left( \frac{\Phi }{2}\right) } \cos{\left( \frac{\Psi }{2}\right) }\\
\cos{\left( \frac{\Theta }{2}\right) } \cos{\left( \frac{\Phi }{2}\right) } \sin{\left( \frac{\Psi }{2}\right) }-\sin{\left( \frac{\Theta }{2}\right) } \sin{\left( \frac{\Phi }{2}\right) } \cos{\left( \frac{\Psi }{2}\right) }\end{pmatrix}
見ての通り、動かしたい順序と演算は逆向きになる。これは、$X$軸に回転を加えると、各々直交している$Y, Z$も方向が変わってしまうため、思いもよらない方向へ回転しまうためである。そのため、最後に動かしたい軸から演算していくことになる。
なお、自身が回転することにより、自身のオブジェクトに直交している座標系も回転することをBody座標系、すなわちローカル座標系、相対座標系という。
相対座標系と対を成すものが絶対座標系(ワールド座標系)である。これはオブジェクトが回転しても軸は変化しない。
XYZ系と書かれている場合Z→Y→Xと計算する。これは回転行列が絶対座標に掛るためである。
相対座標で動かす場合は一軸毎にX→Y→Zと動かすが、これは手で回転を模倣する位しか使わない。
一般的には回転行列で一気に回転を行う。この場合、計算上は上記の問題があるためZ→Y→Xとなる。
換言すると、相対座標X→Y→Zと絶対座標Z→Y→Xは同じ姿勢を表すということである。一般的には相対座標系での表記が使われる。
なんともややこしい。
Y->Z->X系の場合は以下になる。
{\bf R_{yzx} }= R_x \otimes R_{z} \otimes R_{y}=
\begin{pmatrix}\sin{\left( \frac{\Theta }{2}\right) } \sin{\left( \frac{\Phi }{2}\right) } \sin{\left( \frac{\Psi }{2}\right) }+\cos{\left( \frac{\Theta }{2}\right) } \cos{\left( \frac{\Phi }{2}\right) } \cos{\left( \frac{\Psi }{2}\right) }\\
\cos{\left( \frac{\Theta }{2}\right) } \sin{\left( \frac{\Phi }{2}\right) } \cos{\left( \frac{\Psi }{2}\right) }-\sin{\left( \frac{\Theta }{2}\right) } \cos{\left( \frac{\Phi }{2}\right) } \sin{\left( \frac{\Psi }{2}\right) }\\
\sin{\left( \frac{\Theta }{2}\right) } \cos{\left( \frac{\Phi }{2}\right) } \cos{\left( \frac{\Psi }{2}\right) }-\cos{\left( \frac{\Theta }{2}\right) } \sin{\left( \frac{\Phi }{2}\right) } \sin{\left( \frac{\Psi }{2}\right) }\\
\cos{\left( \frac{\Theta }{2}\right) } \cos{\left( \frac{\Phi }{2}\right) } \sin{\left( \frac{\Psi }{2}\right) }+\sin{\left( \frac{\Theta }{2}\right) } \sin{\left( \frac{\Phi }{2}\right) } \cos{\left( \frac{\Psi }{2}\right) }\end{pmatrix}
これら座標系の計算は全てクォータニオンの演算$\otimes$によって行う。
全系について解くのは非常に手間がかかるため、数式処理ソフトを使おう。以下はMaximaの例である。
qq(q,r) := [
q[1]*r[1] - q[2]*r[2] - q[3]*r[3] - q[4]*r[4],
q[1]*r[2] + q[2]*r[1] + q[3]*r[4] - q[4]*r[3] ,
q[1]*r[3] + q[3]*r[1] + q[4]*r[2] - q[2]*r[4] ,
q[1]*r[4] + q[4]*r[1] + q[2]*r[3] - q[3]*r[2]];
cx:cos(Φ/2);
sx:sin(Φ/2);
cy:cos(Θ/2);
sy:sin(Θ/2);
cz:cos(Ψ/2);
sz:sin(Ψ/2);
qx:[cx, sx, 0, 0];
qy:[cy, 0, sy, 0];
qz:[cz, 0, 0, sz];
printf(false,"xyz");
xyz:qq(qq(qz,qy),qx);
a:matrix([xyz[1]], [xyz[2]], [xyz[3]], [xyz[4]]);
Quaternion to Euler Angles + 基軸まわりの回転角
X->Y->Z系による変形の場合は、以下の式から四元数をオイラー角へ復元できる。
{\begin{bmatrix}
\phi\\
\theta\\
\psi
\end{bmatrix}
}=
{\begin{bmatrix}
arctan2(2(q_wq_x+q_yq_z), 1-2(q^2_x+q^2_y))\\
arcsin(2(q_wq_y-q_zq_x))\\
arctan2(2(q_wq_z+q_xq_y), 1-2(q^2_y+q^2_z))
\end{bmatrix}
}
なお、Unity等はZ -> X -> Y系のためこちらは利用できない。
よって回転行列から求めていく。
まず各軸周りの回転行列を以下のように定義する。
z=\begin{pmatrix}\mathit{cosz} & -\mathit{sinz} & 0\\
\mathit{sinz} & \mathit{cosz} & 0\\
0 & 0 & 1\end{pmatrix} \\
x=\begin{pmatrix}1 & 0 & 0\\
0 & \mathit{cosx} & -\mathit{sinx}\\
0 & \mathit{sinx} & \mathit{cosx}\end{pmatrix}\\
y=\begin{pmatrix}\mathit{cosy} & 0 & \mathit{siny}\\
0 & 1 & 0\\
-\mathit{siny} & 0 & \mathit{cosy}\end{pmatrix}
次に、以下を求める
z \cdot x \cdot y = \begin{pmatrix}\mathit{cosy}\, \mathit{cosz}-\mathit{sinx}\, \mathit{siny}\, \mathit{sinz} & -\mathit{cosx}\, \mathit{sinz} & \mathit{cosy}\, \mathit{sinx}\, \mathit{sinz}+\mathit{cosz}\, \mathit{siny}\\
\mathit{cosy}\, \mathit{sinz}+\mathit{cosz}\, \mathit{sinx}\, \mathit{siny} & \mathit{cosx}\, \mathit{cosz} & \mathit{siny}\, \mathit{sinz}-\mathit{cosy}\, \mathit{cosz}\, \mathit{sinx}\\
-\mathit{cosx}\, \mathit{siny} & \mathit{sinx} & \mathit{cosx}\, \mathit{cosy}\end{pmatrix}
なお、行列式を求めたmaximaは以下である。
z: matrix([cosz, -sinz, 0], [sinz, cosz, 0], [0, 0, 1]);
x: matrix([1, 0, 0], [0, cosx, -sinx], [0, sinx, cosx]);
y: matrix([cosy, 0, siny], [0, 1, 0], [-siny, 0, cosy]);
zxy: z . x .y;
次に、この系の回転行列から回転角を抜き出す。まず各軸が独立して動くといった前提から、1つのみの成分を探す。
そうすると、$m_{21}$の$\sin x$が見つかる。これによって$arcsin(sin(x))$が$\theta x$の回転角であることが容易に理解できる。
次に、以下を用いて
\tan = \dfrac{\sin}{\cos}
残りの偏角を見つける。
$m_{01}$と$m_{11}$が条件に当てはまる。よって、
\dfrac{-sinz cosx}{cosz cosx} = -\tan(z)\\
\theta z = arctan2(-sinz, cosz) = arctan2(-m_{01}, m_{11})
と導ける。なお、ここで$cosx$は打ち消し合っている。
最後に$\theta y$は$m_{20}$と$m_{22}$が条件に当てはまる。よって、
\dfrac{-cosx siny}{cosx cosy} = -\tan(z)\\
\theta y = arctan2(-siny, cosy) = arctan2(-m_{20}, m_{22})
なお、この$m_{nm}$は同じ系であればクォータニオンのマトリクスのインデックスと等価である。
よって、クォータニオンによって得られた値を、この中に代入すればよい。
また、$\cos$が0の時の特殊ケースも計算に入れる必要がある。
それをUnityで実装すると以下のようになる。
static Vector3 NormalizeAngles(Vector3 angles)
{
angles.x = NormalizeAngle(angles.x);
angles.y = NormalizeAngle(angles.y);
angles.z = NormalizeAngle(angles.z);
return angles;
}
public static Vector3 FromQ2(Quaternion q1)
{
float sqw = q1.w * q1.w;
float sqx = q1.x * q1.x;
float sqy = q1.y * q1.y;
float sqz = q1.z * q1.z;
float unit = sqx + sqy + sqz + sqw; // if normalised is one, otherwise is correction factor
float test = q1.x * q1.w - q1.y * q1.z;
Vector3 v;
if (test > 0.4995f * unit)
{ // singularity at north pole
v.y = 2f * Mathf.Atan2(q1.y, q1.x);
v.x = Mathf.PI / 2;
v.z = 0;
return NormalizeAngles(v * Mathf.Rad2Deg);
}
if (test < -0.4995f * unit)
{ // singularity at south pole
v.y = -2f * Mathf.Atan2(q1.y, q1.x);
v.x = -Mathf.PI / 2;
v.z = 0;
return NormalizeAngles(v * Mathf.Rad2Deg);
}
Quaternion q = new Quaternion(q1.w, q1.z, q1.x, q1.y);
v.y = (float)Mathf.Atan2(2f * q.x * q.w + 2f * q.y * q.z, 1 - 2f * (q.z * q.z + q.w * q.w)); // Yaw
v.x = (float)Mathf.Asin(2f * (q.x * q.z - q.w * q.y)); // Pitch
v.z = (float)Mathf.Atan2(2f * q.x * q.y + 2f * q.z * q.w, 1 - 2f * (q.y * q.y + q.z * q.z)); // Roll
return NormalizeAngles(v * Mathf.Rad2Deg);
}
2.0 損失関数の設計
姿勢を推定した際に、真の状態からどれくらい離れているかを評価しなければいけない。そのための形式的な手法について触れる。
2.1 オイラー角 (Euler angles)
一番単純な手法に二乗誤差がある。オイラー角ではある任意の回転を表現する$R$は、ほぼ無限に存在している。このため、オイラー角を用いた損失関数は一般的に用いない。仮にオイラー角での評価を行いたい場合は2乗損失誤差を用いることが多いようである。
しかし、周期性の計算が上手く出来ない。例えば、$-30$も$330$も同じ角度のため、こちらの損失について上手く計算してやる必要がある。
これについては後述で述べます。
オイラー角の2乗誤差は以下になる。
E=({\bf R} - \hat{\bf R})^2
=
({\begin{bmatrix}
\phi\\
\theta\\
\psi
\end{bmatrix}
}
-{\begin{bmatrix}
\hat{\phi}\\
\hat{\theta}\\
\hat{\psi}
\end{bmatrix}
})^2
なお、オイラー角で正しく比較したい場合は、向きベクトルから内積を取るとよい。
ただし、オイラー角ではジンバルロックが発生するためクォータニオンが主に用いられている。
2.2 クォータニオン (Quaternion)
クォータニオンの損失関数について説明する。
least square mean
まずPoseNet等でも用いられている手法の1つにLSMがある。こちらも普通に2乗誤差を取るだけである。
E=\dfrac{1}{N}({\bf Q} - \hat{\bf Q})^2
=
({\begin{bmatrix}
q_w\\
q_x\\
q_y\\
q_z
\end{bmatrix}
}
-{\begin{bmatrix}
\hat{q_w}\\
\hat{q_x}\\
\hat{q_y}\\
\hat{q_z}
\end{bmatrix}
})^2
なお、この手法も複数解あるため全く同じ姿勢を表現していても損失が大きくなることがある。
後、幾何学計算的に2乗誤差なのはおかしい。
diff
クォータニオンの特性を生かしたDiffの取り方である。
基本的に誤差の発生がない場合、$(1, 0, 0, 0)$の行列を取る。
よって以下のように損失関数を定義できる。
E={\bf Q}\otimes\hat{\bf Q}^{-1} + (1 - |\hat{q_w}|)
このように共役クォータニオンを掛けることで差分が計算できる。なお、この計算はクォータニオンの演算によって行うこと。
共役の取り方は以下である。
\hat{\bf Q}^{-1} = \dfrac{ (\hat{q_w}, -\hat{q_x}, -\hat{q_y}, -\hat{q_z}) } {\hat{\bf Q} \otimes \hat{\bf Q} }
ここで$\hat{\bf Q} \otimes \hat{\bf Q}$は$\hat{\bf Q}$の長さになる。よって、元から長さが1の場合は行う必要はない。
また、以下の関係式も成り立つ。
\mbox{diff} = {\bf Q}\otimes\hat{\bf Q}^{-1}\\
{\bf Q} \otimes \mbox{diff} = \hat{\bf Q}
この手法を用いた場合は、ジンバルロック等を考えなくてよくなる一方、オイラー角と同様に複数解がある。
同じ向きを向いていたとしても、片方のクォータニオンが物凄くねじれた回転行列の場合は$\mbox{diff}$の値が大きくなる場合がある。
2.3 おまけ:角度の平均や分散
おまけでベイズ推論する際に必要になる平均や分散の求め方についても触れておく。
角度差分
2つの角度が与えられた時にその2つの角度の開きを計算する方法である。普通の引き算では周期性を無視してしまうため、この計算が必要である($359$と$1$度の差は2度である)。
\theta_{diff} = arctan2(\sin (\theta z - \hat{\theta z} ), \cos (\theta z - \hat{\theta z} ))
角度平均
角度の平均の取り方は非常に難しい。なぜなら周期性があるからである。
「角度値単純合算法」と呼ばれる、純粋に角度の値を足して平均を取る方法では$359$と$1$度の平均を取ることさえ上手く行かない。
そこで、演算コストが低く、周期性も考慮できる計算手法に「単位ベクトル合算法」というものがある。
要は度数を単位ベクトルに換算しなおして、長大ベクトルを形成して、最後に平均を取るだけである。
E_{rmean} = arctan2(\dfrac{1}{N}\Sigma \sin(\theta), \dfrac{1}{N}\Sigma \cos(\theta))
これで$359$と$1$度の平均は0となる。
単位ベクトル合算法の問題点
単位ベクトル合算法では総和を取った後に割り算を行うのであるが、この処理に大きな問題がある。
例えば、円の定義は$\sin^2 \theta + \cos^2 \theta = 1$である。
この制約がある数式に対して総和を取って割り算を行うと、おかしなことになるのは直感的に理解できる。
最終的には単位ベクトル合算法は±1σの誤差が乗っかる。
$(0, 0, 90)$の角度が与えられた時を考える、これらの平均を取ると$(0 + 0 + 90)/3=30$となる。
これは正しい答えである。では、ベクトル平均法によって計算するとどうなるだろうか。
$\sin(0) = 0$及び$\cos(0) = 1$なことから、$\sin(90) = 1$及び$\cos(90) = 0$から以下のようなグラフを描ける。
よって、ベクトル平均法によって計算すると$\sin(2/3), \cos(1/3)$の$arctan2$を計算することになる。
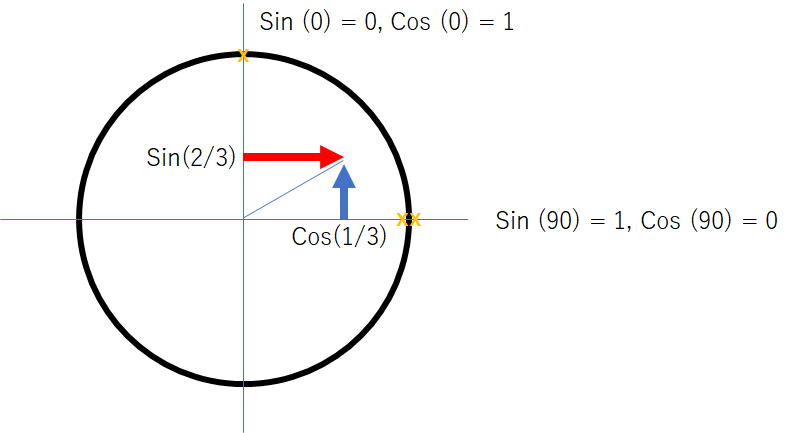
どう考えても単位円上に乗っていない。因みに、この状態のベクトル平均は$26.565$度である。
このような問題は、角度のデータセットがバラけている程起こりやすくなる。
また、平均0度の時にも上手く計算できず、$arctan2(0, 0) = 0$度という結果を出してしまう。
この辺については中心極限定理あたりの理論を勉強する必要がある。
単位ベクトル合算法の分散
単位ベクトル合算法では、その性質上大きなエラーを孕むことが分かった。
ではこれを計算出来ないか?
単位ベクトル合算法ではベクトルを足し合わせていくので、同じ向き方向であれば、純粋にそれは$\alpha\sin^2 \theta + \alpha\cos^2 \theta = \alpha1$となる。
よって平均を取ると長さが1になる。対して、各々がバラバラの方向、最大でいえば真逆を向いていれば長さは0となる。
よって、分散値が高い状態を平均合成ベクトルの長さで以下のように定義できる。
R= 1 - ((\dfrac{1}{N}\Sigma \sin(\theta))^2 + (\dfrac{1}{N}\Sigma \cos(\theta))^2)
この手法によって、$(0, 0, 90)$度に対して分散値を得ると$0.444$となった。
真値は$30$度、単位ベクトル合算法平均値$26.56505$度、単位ベクトル合算法分散値$0.444$である。
単位ベクトル合算法のばらつき指標
なお、分散指標を取る場合は以下の数式で表現できる。
\delta = \dfrac{1 - ((\dfrac{1}{N}\Sigma \sin(2 \cdot \theta))^2 + (\dfrac{1}{N}\Sigma \cos(2 \cdot \theta))^2)}
{2 \cdot ((\dfrac{1}{N}\Sigma \sin(\theta))^2 + (\dfrac{1}{N}\Sigma \cos(\theta))^2)^2}
単位ベクトル合算法の平均合成ベクトルの角度を2倍にしたものを平均合成ベクトルの2乗したもので割るだけである。
単位ベクトル合算法の標準誤差
標準誤差は平方根を取って直感的に誤差を分かりやすい値にする。
\delta_{std} = \sqrt{-2\log{(\dfrac{1}{N}\Sigma \sin(\theta))^2 + (\dfrac{1}{N}\Sigma \cos(\theta))}}
これらのプログラムを作成したPythonコードは以下である。
radAry = np.deg2rad([0, 0, 90])
ms = np.sum(np.sin(radAry))/len(radAry)
mc = np.sum(np.cos(radAry))/len(radAry)
R = (ms ** 2 + mc ** 2)
var = 1 - R
print(np.rad2deg(np.arctan2(ms, mc)))
print( "circular variance:" + str(var))
print( "circular std:" + str(np.sqrt((-2*np.log(R)))))
ms2 = np.sum(np.sin(radAry * 2))/len(radAry)
mc2 = np.sum(np.cos(radAry * 2))/len(radAry)
R2 = (ms ** 2 + mc ** 2)
disp = (1 - R2) / (2 * R*R)
print( "circular dispersion:" + str(disp) )
分散方程式を用いた角度分散
分散方程式に角度の差分と平均値を用いて計算する。こちらの方が直感的に分かりやすい。
しかし、正しい平均値で計算する必要がある。
E^2_{s} =\frac{1}{n}\sum_{i=1}^n arctan2(\sin (\hat{\theta z} - E_{rmean} ), \cos (\hat{\theta z} - E_{rmean} ))^2
これで分散値の計算が可能である。なお、他にも数種類あるようではある。
終わり
終わり。本当はもっと書きたかったけどQiitaが重すぎてこれ以上書けない。
あと、中学生には少し複雑だった。