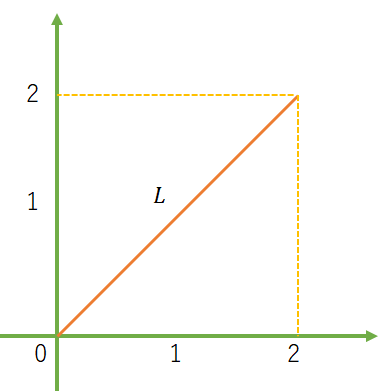0. 概要
変分法等を不自由なく扱うためには媒介変数、陽関数、陰関数表示等の中学生数学が必要である。
このため、これら足回りの道具について簡単に触れていく。
1. 曲線の長さ
媒介変数、陽関数、陰関数表示を行う際の例題を曲線の長さとする。
これは一般的に良く用いられる例題で理解がたやすい。
1.1. 微分
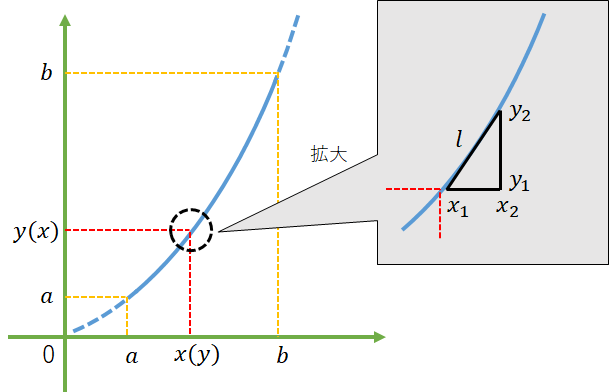
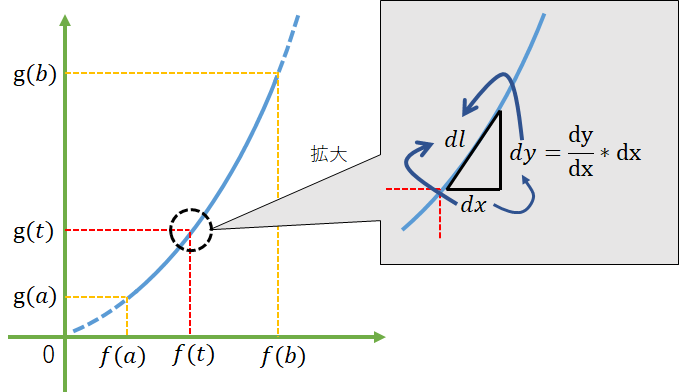
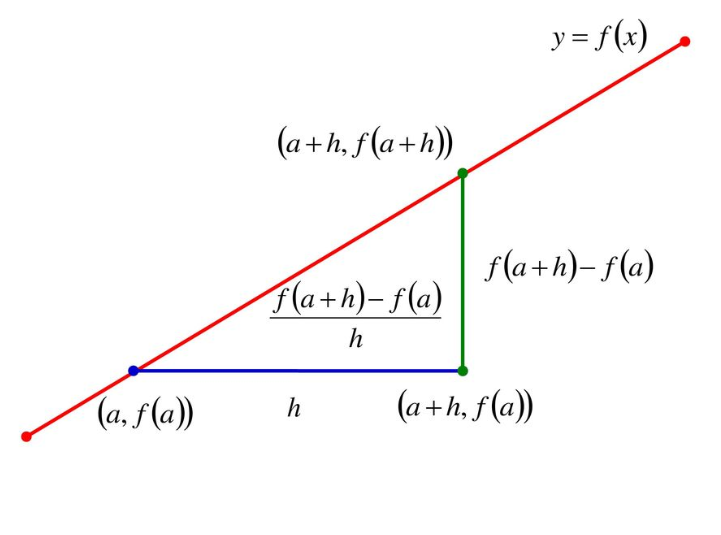
まず、線分におけるある極小な2点間のの距離を考える。言い換えると、図の曲線が与えられた時に赤い点線が指すグラフの勾配を考える。
この微分を求めるということは直線を求めることと等価である。
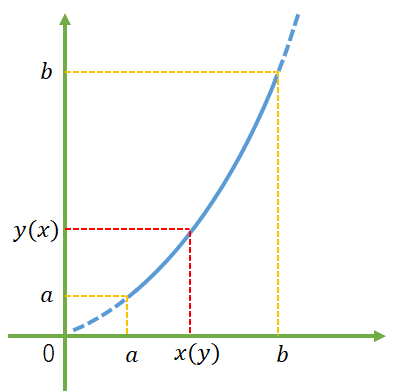
$y(x)$とは、$x$が与えられた時に$y$が定まるという意味であり、直線の方程式は$y=ax+b$であるため、微分値は$a$となる。
よって、初期値の$b$を取り除き、式を$a$周りに変形すると
y=ax\\
a=\dfrac{y}{x}
となり、$x$が移動量、$y$が変化量でよく見るパターンの微分式になる。図で表すと以下になる。
一般的には$x=h$、$y=f(a+h)-f(a)$と置き換えられ、$a=\dfrac{f(a+h)-f(a)}{h}$と表記される。
1.2. 2点間の距離
微分はグラフ上のとある場所の勾配を知る方法であった。
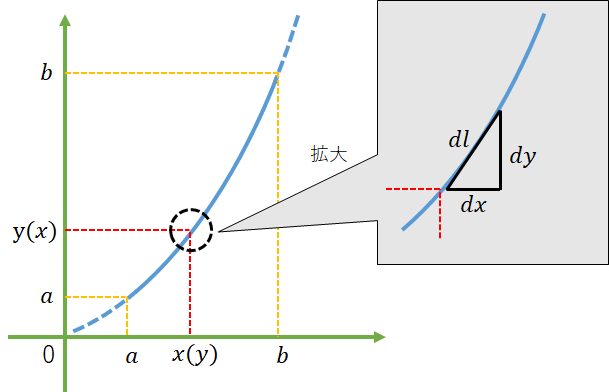
次に積分等でグラフ全体を表現したい場合に2点間の距離を求め、積算する場合がある。これは、微分を線で扱うようなものである。
図で表現すると以下である。求めたいのは$l$である。
$l$は三平方の定理で容易に求められる。
l^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2
この時、$(x_2 - x_1)$、$(y_2 - y_1)$及び$l$はある場所の変化量、長さを示しているので、以下のように書かれる場合が多い。
(x_2 - x_1) = dx = \Delta x \\
(y_2 - y_1) = dy = \Delta y \\
l = dl = \Delta l \\
これらをまとめると、2点間の距離は以下のように求められる。
dl^2 = (dx)^2 + (dy)^2 \\
dl = \sqrt{(dx)^2 + (dy)^2}
後は、積分で全区間を求めればグラフの曲線の長さが求まる。
L =\int ^{b}_{a} dl
1.2. 媒介変数表示
媒介変数表示とは、これまで$x, y$等で表現出来ていたものを$t$等で置き換えて表現しなおすことである。
例えば、$y(x)$は$x$によって値が決まっていたが、これを$t$に置き換える。
その場合、$x$も$t$で置き換えなければならないので、以下のようにする。
y = t * 2\\
x = t
他の例としては単位円を$x^2 + y^2 = 1$で表現するとき、$x, y$の代わりに$\theta$を用いるのも媒介変数表示である。
x = cos \theta \\
y = sin \theta
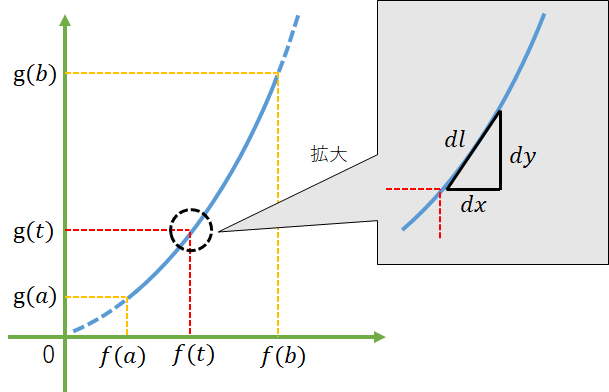
では本題で、曲線$L$上の点$P(x, y)$を媒介変数$t$を用いて以下のように表現する。
すなわち、こうなる。
x=f(t)\\
y=g(t)
この時、$t$は$(a \leqq t \leqq b)$の範囲である。
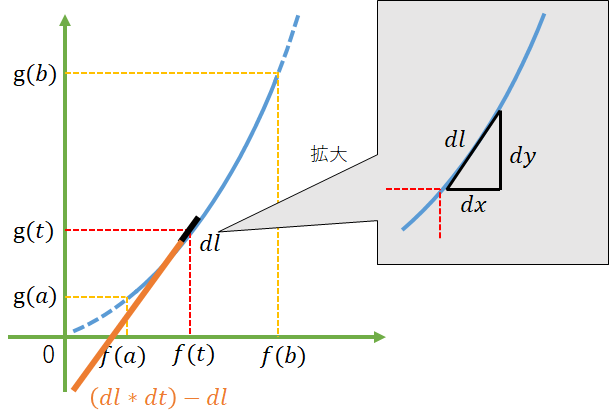
$dl$を求めたい場合は、$x$のある区間を媒介変数$t$で指定することとなる。これを$\dfrac{dx}{dt}$のように微分形式で表現する。
$\dfrac{dx}{dt}$は$x$のある範囲を$t$で指定しているだけに過ぎない
$y$も同様に媒介変数表示し、式を整理すると以下のようになる。
dl = \sqrt{(\dfrac{dx}{dt})^2 + (\dfrac{dy}{dt})^2} dt
最後に$dt$がつくのは、ある地点$t$の2点間の距離を、開始地点からある地点$t$までを含んだ距離に変換しているだけである。
よって、全曲線の求め方は以下となる。
L = \int_{a}^{b} \sqrt{(\dfrac{dx}{dt})^2 + (\dfrac{dy}{dt})^2} dt
例題
ここで、$x=t$、$y=t$を媒介変数表示とする。また、範囲は$a = 0$、$b = 2$とする。
まず、答えを三平方の定理で出すと
l^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2 \\
L^2 = (2-0)^2 + (2-0)^2 \\
= \sqrt{8} = 2.828
次に、以下の媒介変数表示の式を用いて求めてみる。
L = \int_{a}^{b} \sqrt{(\dfrac{dx}{dt})^2 + (\dfrac{dy}{dt})^2} dt
値を入れると、
L = \int_{0}^{2} \sqrt{(\dfrac{dx}{dt})^2 + (\dfrac{dy}{dt})^2} dt = [\sqrt{(\dfrac{2}{2})^2 + (\dfrac{2}{2})^2} * 2] - [0] = 2.828
1.3. 陽関数表示
陽関数表示とは$y=f(x)$のように$y$で式を整理することである。陰関数は$y-f(x)=0$という形である。
では陽関数表示で曲線の長さ$L$を表してみる。
$y=f(x)$を用いる。これまで$x=f(t)$だった、これは$t$によって$x$が定まるというもの。
このため、$y=f(x)$は$x$によって$y$が定まるといえる。
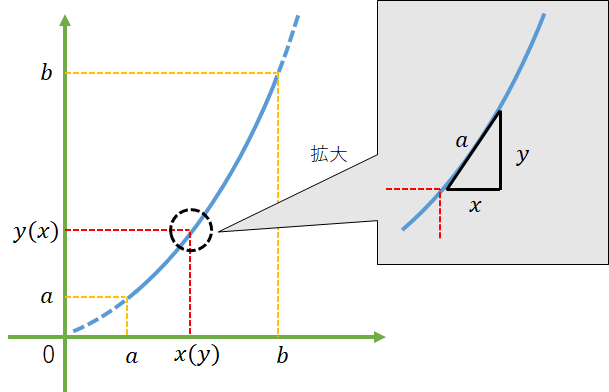
式展開は簡単で、以下のようになる。無駄な$t$が無くなったと思えばよい。
dl = \sqrt{(\dfrac{dx}{dx})^2 + (\dfrac{dy}{dx})^2} = \sqrt{1 + (\dfrac{dy}{dx})^2}dx
図だとこのようになる。
曲線の積分は以下のようになる。
L = \int_{a}^{b} \sqrt{1 + (\dfrac{dy}{dx})^2} dx
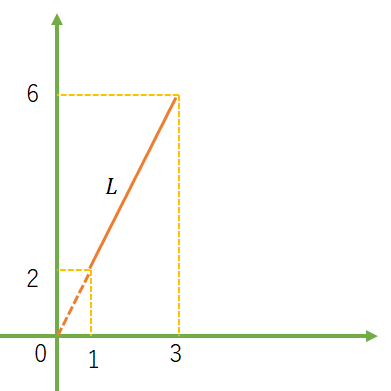
例題
まず、全体の長さを求めて、そこから点線の部分を引くだけである。
答えは、三平方の定理から$\sqrt{(6-2)^2 + (3-1) ^2}=4.472$である。
では、以下の公式を用いる。
L = \int_{a}^{b} \sqrt{1 + (\dfrac{dy}{dx})^2} dx
図の値を入れて、
L = \int_{1}^{3} \sqrt{1 + (\dfrac{dy}{dx})^2} dx\\
= [(1 + (\dfrac{6}{3})^2) \cdot 3] - [1 + (\dfrac{2}{1})^2 \cdot 1] \\
= 6.7082039 - 2.23606\\
= 4.472
一致した。
ここで、混乱するかもしれないが、図の$dy$という領域は数式では$\dfrac{dy}{dx}$と表現されているが、具体的な処理は$\dfrac{y}{x}$を行えばよい。ある$x$地点における$y$の勾配を$\dfrac{dy}{dx}$と表現しているだけにすぎない。
1.4. 極座標表示
媒介変数に$\theta$を選ぶと極座標形式にもできる。
x= r cos \theta \\
y= r sin \theta
これから、
\dfrac{dx}{d\theta} = \dfrac{dr}{d\theta} cos \theta + r (-sin \theta) \\
\dfrac{dy}{d\theta} = \dfrac{dr}{d\theta} sin \theta + r cos \theta
$(\dfrac{dx}{d\theta})^2 + (\dfrac{dy}{d\theta})^2$から各々を二乗して、
\dfrac{dr}{d\theta}^2cos^{2}\theta - 2\dfrac{dr}{d\theta}r\theta sin \theta cos \theta + r^{2}sin^{2} \theta\\
+ \dfrac{dr}{d\theta}^2sin^{2}\theta - 2\dfrac{dr}{d\theta}r\theta sin \theta cos \theta + r^{2}cos^{2} \theta\\
= \dfrac{dr}{d\theta}^2 + r^2
よって、
L = \int_{a}^{b} \sqrt{r^2 + (\dfrac{dr}{d\theta})^2} d\theta
となる。