0. 概要
統計学的なアプローチの中で最小二乗法の次あたりに出てくる最尤推定を理解する。
最尤推定では、あるデータセットから、それを表現するための関数の係数をフィッティングすることができる。
これに加えて、フィッティングした関数と真値との分散も表現することができる。
因みに、数式を展開していくと、
「ある基底を持った線形結合の推論」+「データセット全体に対する標準偏差」の計算となる。
後者が一般的な最適化計算と比較して統計学らしい部分である。
1. 理論
理論について簡単に説明する。
なお、最尤推定では実際に観測されたデータは発生確率が一番高いという前提がある。
ガウス基底
あるデータセット$x$を表現する関数が$f(x)$の時、その$f(x)$と真値の誤差は以下で表現できる。
そう、言わずもがなの2乗誤差である。
E=\displaystyle\sum_{i}\{y_i-f(x_i)\}^2
次に、ガウス基底が以下のように与えられる。
{\phi_i(x)=\exp\left\{-\frac{(x-c_i)^2}{2s^2}\right\}\hspace{1.0em}(i=0,\cdots,M-1)\hspace{1.0em}}
この時、$c_i$は中心地を表す。すなわち、正規分布の中心地、山の中心である。以下は0。
因みに、$s$は分散を示し、大きければ大きいほど、遠くまでのデータに影響を与える。
最尤推定の定義
次に、このガウス基底を「ガウス分布による最尤推定の形に書き直す」と以下のように定義できる。
{\mathscr N}(t|\mu,\sigma^2) := \frac{1}{\sqrt{2\pi \sigma^2}}\exp\left\{-\frac{1}{2\sigma^2}(t-\mu)^2\right\} \\
※$A:=B$はAをBによって定義するという意味
この時、$u$は平均、$\sigma^2$は分散を示す。正規分布の平均値は山なりの部分、すなわち推定値として最も確率の高い数値を示す。
よって、以下のように$u$を$f(x)$として表記できる。
{\mathscr N}(t|f(x),\sigma^2) := \frac{1}{\sqrt{2\pi \sigma^2}}\exp\left\{-\frac{1}{2\sigma^2}(t-f(x))^2\right\} \\
そして、$f(x)$は重み$w$を持ち、分散を$\sigma^2=\beta^{-1}$と表記する慣例に倣うと以下のように整理できる。
{\mathscr N}(t|f(x, \mathbf w), \beta^{-1}) := \frac{1}{\sqrt{2\pi \beta^{-1}}}\exp\left\{-\frac{1}{2\beta^{-1}}(t-f(x, \mathbf w))^2\right\} \\
ここでは、$x$は固定されており、$w$はベクトルを持つ。
この式を文章にするなら、分散$\beta^{-1}$とパラメータ$w$、入力$x$が与えられた時、目的変数$t$になる確率密度を計算することになる。
見て分かる通り、フィッティングする関数$f(x, w)$の中心地がガウス分布の中心地になっている。
すなわち、確率的に最も高い予測値を中心とした正規分布の平均値$u$であることが分かる。
言い換えると、ある$x$を見た時に、それに対応する最も確率の高い$t$を出力することである。
最尤推定の損失関数
次に、どのようにフィッティングするかを考える。
まず、最尤推定の定義は以下である。
{\mathscr N}(t|f(x, \mathbf w), \beta^{-1}) := \frac{1}{\sqrt{2\pi \beta^{-1}}}\exp\left\{-\frac{1}{2\beta^{-1}}(t-f(x, \mathbf w))^2\right\} \\
次に、与えられる$x, t$はデータセットであるわけだから、$x, t$をベクトルにして計算する。
p({\mathbf t} | {\mathbf x},{\mathbf w},\beta) = \prod_{n=1}^N{\mathscr N}\left(t_n\,\middle|\,f(x_n,{\mathbf w}),\beta^{-1}\right)
この時、それがどのくらいの確率で発生するかの計算のため、$\sum$ではなく$\prod$になる。
イメージ的には各データ点の分布において頂点(平均値)となる確率を選び続ける確率を計算している。
後は残りの式を展開すると以下のようになる。
p({\mathbf t} | {\mathbf x},{\mathbf w},\beta) =\left(\frac{\beta}{2\pi}\right)^{\frac{N}{2}}\exp\left\{-\frac{\beta}{2}\sum_{n=1}^N\left(f(x_n,{\mathbf w})-t_n\right)^2\right\}\
次に損失関数のみ外に出して書くと、以下のように変形できる。
p({\mathbf t} | {\mathbf x},{\mathbf w},\beta) = \left(\frac{\beta}{2\pi}\right)^{\frac{N}{2}}\exp\left\{-\beta E_{\rm D}({\mathbf w})\right\}\\
E_{\rm D}({\mathbf w}) := \frac{1}{2}\sum_{n=1}^N\left(f(x_n,{\mathbf w})-t_n\right)^2
最尤推定の尤度関数 (損失関数の続き)
観測されたデータ$t$は発生確率が一番高いという前提があるため、$t$すなわち$p({\mathbf t} | {\mathbf x},{\mathbf w},\beta)$が正規分布の山の頂点に(値が最も大きく)なるような$\mathbf w, \beta$を取らなければいけない。ようは、入力$x$に対して答え$t$の確率が高く出力される分布を得られるようにするということである。
このため$p({\mathbf t} | {\mathbf x},{\mathbf w},\beta)$は$(\mathbf w, \beta)$の関数とみなすことができ、これを尤度関数と呼ぶ。
次に、簡単のため、以下の関数を対数尤度関数に変形し、最大化できるようにする。
p({\mathbf t} | {\mathbf x},{\mathbf w},\beta) = \left(\frac{\beta}{2\pi}\right)^{\frac{N}{2}}\exp\left\{-\beta E_{\rm D}({\mathbf w})\right\}\\
変形すると、$\ln p=$の形に整理できる。
\ln p({\mathbf t} | {\mathbf x},{\mathbf w},\beta)=-\beta E_{\rm D}({\mathbf w})+\frac{N}{2}\ln\beta-\frac{N}{2}\ln(2\pi)
この時、$\mathbf w, \beta$がパラメータであり、このパラメータの勾配を0にすることが収束条件となる。
wの関係式
まず$\mathbf w$であるが、こちらは2乗誤差の損失関数$E_{\rm D}({\mathbf w}) $でしか参照されていない。
参考:
p({\mathbf t} | {\mathbf x},{\mathbf w},\beta) = \left(\frac{\beta}{2\pi}\right)^{\frac{N}{2}}\exp\left\{-\beta E_{\rm D}({\mathbf w})\right\}\\
\ln p({\mathbf t} | {\mathbf x},{\mathbf w},\beta)=-\beta E_{\rm D}({\mathbf w})+\frac{N}{2}\ln\beta-\frac{N}{2}\ln(2\pi)\\
E_{\rm D}({\mathbf w}) := \frac{1}{2}\sum_{n=1}^N\left(f(x_n,{\mathbf w})-t_n\right)^2
よって、$w$が用いられている以下の偏微分(最小二乗法)の結果、勾配が0になれば良いということである。
\frac{\partial E_{\rm D}}{\partial {\mathbf w}} = 0
これで、損失関数は最小二乗そのものであることが分かった。
βの関係式
次に、$\beta$を偏微分して勾配を0にすることを考える。
\frac{p({\mathbf t} | {\mathbf x},{\mathbf w},\beta)}{\partial {\beta}} = 0
この偏微分を展開すると以下のようになる。
\frac{p({\mathbf t} | {\mathbf x},{\mathbf w},\beta)}{\partial {\beta}} = E_{\rm D}({\mathbf w})
なんと損失関数が出てきた。加えて、元の損失関数は偏微分をしやすいように$\dfrac{1}{2}$になっているため、
こちらを分散を求めるように$\dfrac{1}{N}$にする。
\beta^{-1}=\frac{1}{N}\sum_{n=1}^N\left\{f(x_n,{\mathbf w})-t_n\right\}^2
この式はトレーニングデータの分散は、新しく入力されるデータの推定値に対する誤差(分散)として使えるということを言っている。
これによって、$\mathbf w$と$\beta$の求め方が分かった。
フィッティング
損失関数$E_{\rm D}({\mathbf w})$を最小化することによって、$\mathbf w, \beta$の両方を最小化できることがわかった。このため、この損失関数に対して最急降下法等で最適化していけばよい。
しかし、多項式、ガウス基底の解析解は以下のように求められるため、オプティマイザーを使う必要はない。
※使ってもいい
結局は基底の線形結合なので、ヴァンデルモンドの行列を用いれば簡単に解を得られる。
$f(x)$の$w$は以下により解析的に求められる。
w=(x^Tx)^{-1}x^{T}y
次に、平均値$f(x)$及び分散$\beta^{-1}$を計算する。
f(x) = \dfrac{1}{n}(x^M_1+x^M_2+\cdots+x^M_n)=\overline x = \mu
\beta^{-1} = \dfrac{1}{n}\left\{(x^M_1-\overline x)^2 + (x^M_2-\overline x)^2 + \cdots + (x^M_n-\overline x)^2 \right\} = \nu
ここで、$\overline x$の真値は教師すなわち$t$であることを忘れてはいけない。
よって、この計算で用いる$\overline x$は各データ点の教師と予測した値の分散である。
2. 実装
1データとデータセットに対するフィッティングを行う。
1データ点に対するフィッティング
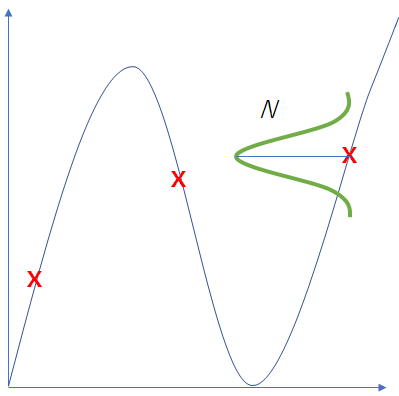
問題を簡単化し、まずは以下の緑色の分布だけを得ることを考える。
ある$x$の地点の分布を得るためには、各データの平均値すなわち中心点$u$と、データの分散$\beta^{-1}$を計算する必要がある。
なお、距離によってエラーを取る場合、端っこの方はデータ個数が少なく、距離に開きが生じにくい問題がある。
このため、各データ点に対する分散の重みを勘案してあげると均等な分散の計算になる。
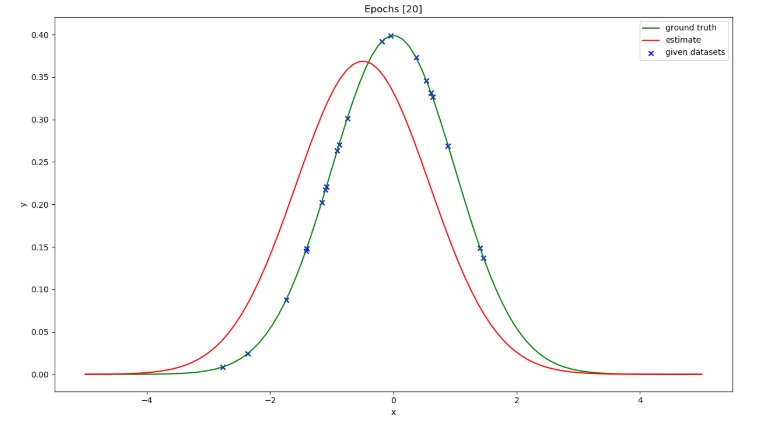
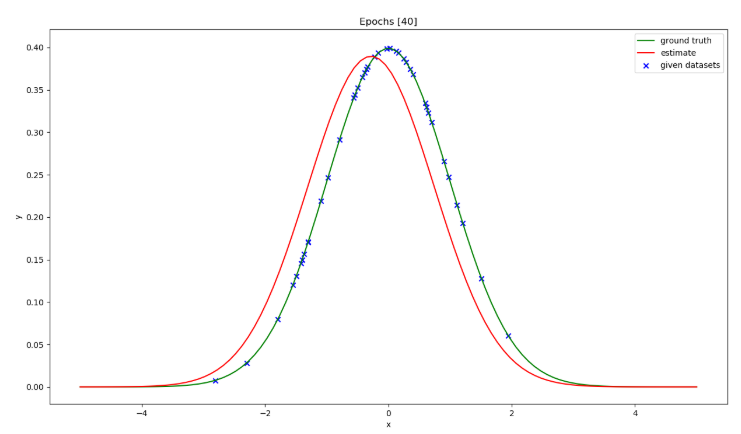
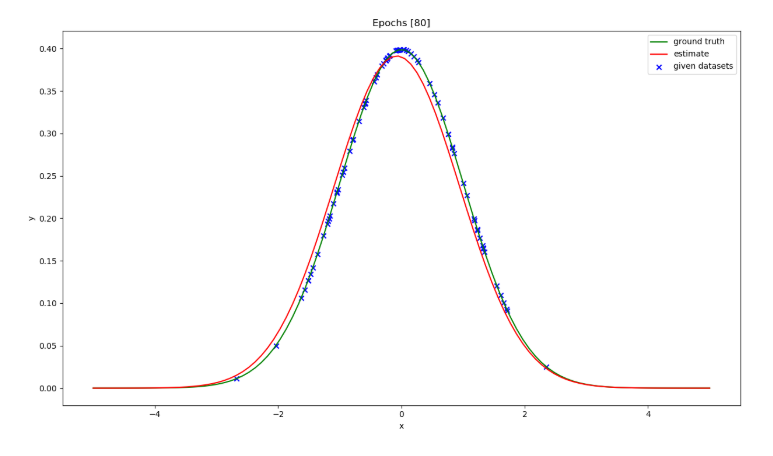
データ点20個の場合は、推定精度が低い。
import numpy as np
import matplotlib as mpl
mpl.use('Agg')
import matplotlib.pyplot as plt
from numpy.random import normal
from scipy.stats import norm
#################################################################
## Fields,
#################################################################
train_size = 32
noise = 1.0
#########################################
# Figure
#########################################
ax = []
plt.clf()
ax_count = 1
max_plot_num = 5
indx = 10
fig = plt.figure(figsize=(15, 75))
fig.subplots_adjust(hspace=1)
#########################################
# Training data
#########################################
for i in range(20, 101, 20):
print(i)
dataset = normal(loc=0, scale=1, size=i)
# plot
ax.append(fig.add_subplot((max_plot_num), 1, ax_count))
ax[-1].set_xlabel('x')
ax[-1].set_ylabel('y')
ax[-1].set_title('Epochs [%d]' % i)
# norm dist.
xdata = np.linspace(-5.0, 5.0, 100)
orig = norm(loc=0, scale=1)
ax[-1].plot(xdata, orig.pdf(xdata), color='green', label='ground truth')
# dataset
ax[-1].scatter(dataset, orig.pdf(dataset), marker='x', color='blue', label="given datasets")
# estimate
t_hat = np.mean(dataset) # mu
beta = np.sqrt(np.var(dataset))
est = norm(loc=t_hat, scale=np.sqrt(beta))
ax[-1].plot(xdata, est.pdf(xdata), color='red', label="estimate")
plt.legend()
ax_count += 1
plt.savefig( 'trainingData.png' )
複数データ点に対するフィッティング
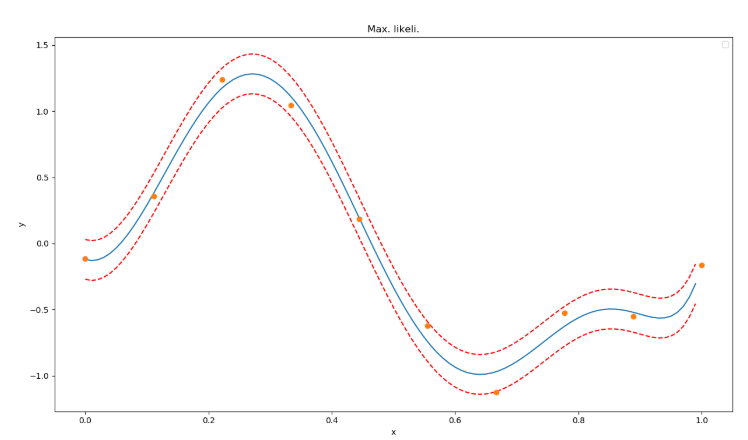
実装方法としては非常に簡単でガウス基底回帰を解いて、そのあとに推論結果と教師データ全体の誤差を計算する。
これはデータセットに対して行う。
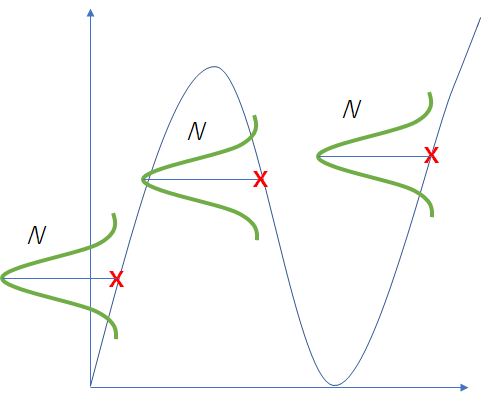
すなわち、この図のように複数の分布を包括的に計算する。
実装は以下である。
import numpy as np
import math
from scipy.optimize import minimize
#################################################################
## Fields,
#################################################################
X = np.linspace(0, 1, 10)
t = np.sin(2*np.pi*X) + np.random.normal(0, 0.2, X.size)
#########################################
# Estimate
#########################################
def phi(x):
m = 8
return x ** np.arange(0, m)
PHI = np.array([phi(x) for x in X])
w = np.dot(np.linalg.inv(np.dot(PHI.T, PHI)), np.dot(PHI.T, t))
#########################################
# Calc
#########################################
xlist = np.arange(0, 1, 0.01)
ylist = [np.dot(w, phi(x)) for x in xlist]
y_hat = [np.dot(w, phi(x)) for x in X]
sums = np.sum( (y_hat - t) ** 2 )
beta = np.sqrt(1.0 / len(t) * sums) # std
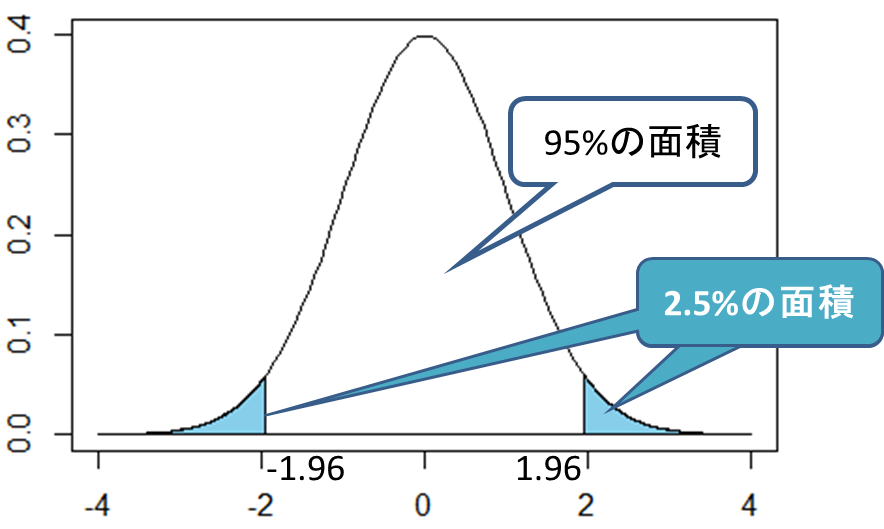
lowers = np.array(ylist) - 1.96 * beta
uppers = np.array(ylist) + 1.96 * beta
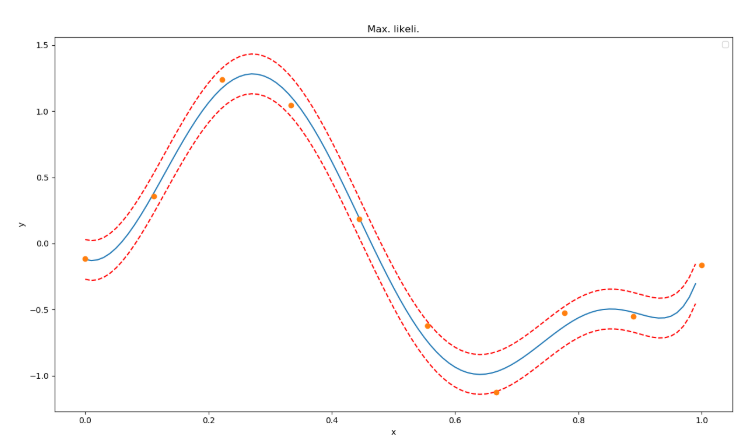
画像化すると以下のような結果が得られる。
各サンプルは95%の信頼区間に収まっていることが確認できる。