機械学習で用いる行列の単語を整理した② (分散共分散行列、相関行列)

分散共分散行列

言葉の通り、分散＋共分散の意味を持つ。複数の分散がどのような相関を持つのかを求められる。

分散とは、与えられたデータに対して、どれくらいばらつきがあるかを示す指標である。標準偏差等と非常に似ている。

数式で表すと偏差(各値―平均値)を2乗し足し足し合わせて、平均を取る。

分散:

s^{2}=\dfrac {1}{n}\sum ^{n}_{n=1}\left( x_{i}-\overline {x}\right) ^{2}

誤差が2乗の積和のため、感覚的に直値との差が分からない。

標準偏差:

s=\sqrt{\dfrac {1}{n}\sum ^{n}_{n=1}\left( x_{i}-\overline {x}\right) ^{2}}

誤差の平方根を取るため、感覚的に直値との差が分かる。

分散は1つのデータ群からばらつきを示す指標である。例えば、1学年の数学の点数が沢山与えられて、どれくらい点数にばらつきがあるかを見たいとき等に使う。

ここで、標本(データ)が2つの群から形成され、その関係性を見たい場合に共分散を用いる。

例えば、生徒の「数学」と「理科」の点数がそれぞれ与えられたとする。その時に共分散を求めることで、数学が出来る人は理科もできる（正値になる）。もしくは数学が出来る人は理科が出来ない（不値になる）といった関係性を求められる。

計算的には「数学の点数―数学の平均値」と「理科の点数―理科の平均値」を掛け合わせればよい。

共分散(標本共分散行列):

cov=\dfrac {1}{n}\sum ^{n}_{i=1}\left( x_{i}-\overline {x}\right) \left( y_{i}-\overline {y}\right) ^{T}

共分散(不偏共分散行列):

cov=\dfrac {1}{n-1}\sum ^{n}_{i=1}\left( x_{i}-\overline {x}\right) \left( y_{i}-\overline {y}\right) ^{T}

※一般的には標本共分散行列を用いる。

次に、共分散行列の「行列」を考える。
共分散行列は以下のように定義され、実対象行列である。

\Sigma=\begin{bmatrix}
cov_{xx} & cov_{xy} \\
cov_{yx} & cov_{yy}
\end{bmatrix}
=\begin{bmatrix}
s^{2}_{xx} & cov_{xy} \\
cov_{yx} & s^{2}_{yy}
\end{bmatrix}

ここで、$\Sigma$は共分散行列を示す。$s^2_{xx}$は$x$の分散を示す。$cov_{xy}$は$x$と$y$の共分散を示す。
共分散$cov_{xx}$は$x$の分散を計算しているのと同じ処理になる。

なお、例は2次元であるが、3次元も$x, y, z$の組が増えていくだけである。

計算

ここで生徒3人の国語、数学、理科の得点が次のように与えられたとする

math: x = \begin{bmatrix}
80 & 20 & 50
\end{bmatrix}

science: y =\begin{bmatrix}
100 & 30 & 80
\end{bmatrix}

lang: z =\begin{bmatrix}
50 & 50 & 50
\end{bmatrix}

次式の行列式を解き、共分散行列を求める。

\Sigma=\begin{bmatrix}
cov_{xx} & cov_{xy} & cov_{xz} \\
cov_{yx} & cov_{yy} & cov_{yz} \\
cov_{zx} & cov_{zy} & cov_{zz}
\end{bmatrix}
=\begin{bmatrix}
s^{2}_{xx} & cov_{xy}   & cov_{xz} \\
cov_{yx}   & s^{2}_{yy} & cov_{yz} \\
cov_{zx}   & cov_{zy}   & s^{2}_{zz}
\end{bmatrix}

まずは対角成分を求める。

$xx$の分散について求める

mean_{math} = \frac{1}{3}(80 + 20 + 50) = 50

cov_{xx} = s^{2}_{xx}  = \frac{1}{3} \left\{ (80-50)^{2} + (20-50)^{2} + (50-50)^{2} \right\} = \frac{1800}{3} = 600

同様に、$yy$と$zz$を求める

cov_{yy} = s^{2}_{yy}  = 866.667

cov_{zz} = s^{2}_{zz}  = 0

次に共分散の$xy$成分を求める。

cov_{xy} = 
\dfrac {1}{n}
\sum ^{n}_{i=1}
\left( x_{i}-\overline {x}\right) \left( y_{i}-\overline {y}\right) ^{T}
=\dfrac {1}{3}
\left\{ (80 - 50), (20 - 50), (50 - 50) \right\} 
\left\{ (100 - 70), (30 - 70), (80 - 70) \right\} ^{T}
\\
=\dfrac {1}{3}det\left\{
\left[ 30, -30, 0 \right]
\begin{bmatrix}
30 \\
-40 \\
10
\end{bmatrix} \right\} = \dfrac {1}{3} * 2100 = 700

同様に$xz$～$zy$までを求める

cov_{xz} = 0 \\
cov_{yx} = 700 \\
cov_{yz} = 0 \\
cov_{zx} = 0 \\
cov_{zy} = 0 \\

よって、以下の行列が得られた。

\Sigma=\begin{bmatrix}
600 & 700 & 0 \\
700 & 866.667 & 0 \\
0 & 0 & 0
\end{bmatrix}

これから、数学と理科の相関は700と大きな値を示し、国語と数学/理科の相関は少ないということが分かった。

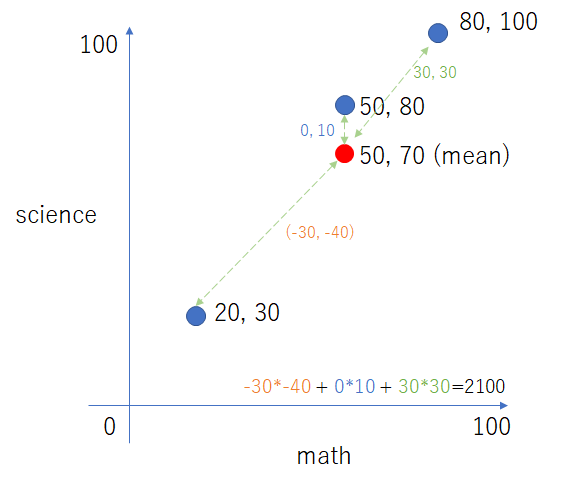
イメージ

数学と科学との分散共分散行列をイメージ化すると以下である。
結局は平均値と各要素の距離を取っているだけにすぎない。これはマハラノビス距離等でも出てくる。

コード

import numpy as np

A = np.array([
              [80, 20, 50], # math
              [100, 30, 80], # science
              [50, 50, 50] # lang
              ])

print(np.var(A[0])) # xx
print(np.var(A[1])) # yy
print(np.var(A[2])) # zz

# xy = yx
a = A[0] - np.mean(A[0])
b = A[1] - np.mean(A[1])
print("---------")
print( 1/3 * np.dot(a, b.T)) 
print(np.cov(A, bias=True))

相関行列 (基準化)

標本(データ)が2つ以上の群から形成され、その関係性を見たい場合に相関係数を用いる。
共分散行列と殆ど使い勝手は同じであるが、こちらは$-1～+1$の範囲で正規化（基準化）されている。
$1$が最も相関があり$-1$は負の相関がある。$0$が最も相関がない。

共分散行列で求めた値を基準化するため標準偏差で割るだけである。
割り算が発生するため、標準偏差が$0$になる計算には使えない。

共分散は誤差を2乗及び平方根を取らないため、符号が残る。標準偏差は誤差を2乗して平方根を取るため、符号が残る。
すなわち、$xx$の共分散と標準偏差は同じ値を示すため、$1$になる。よって、対角成分は全て$1$である。

数式は以下である。

corr = \dfrac{\dfrac {1}{n}\sum ^{n}_{i=1}=\left( x_{i}-\overline {x}\right) \left( y_{i}-\overline {y}\right) ^{T}}{\sqrt {\dfrac {1}{n}\sum ^{n}_{i=0}\left( x_{i}-\overline {x}\right) ^{2}} \sqrt {\dfrac {1}{n}\sum ^{n}_{i=0}\left( y_{i}-\overline {y}\right) ^{2}}}

相関行列は以下で計算する。

corr_{mat}=\begin{bmatrix}
corr_{xx} & corr_{xy} & corr_{xz} \\
corr_{yx} & corr_{yy} & corr_{yz} \\
corr_{zx} & corr_{zy} & corr_{zz}
\end{bmatrix}

計算

ここで生徒3人の国語、数学、理科の得点が次のように与えられたとする

math: x = \begin{bmatrix}
80 & 20 & 50
\end{bmatrix}

science: y =\begin{bmatrix}
100 & 30 & 80
\end{bmatrix}

lang: z =\begin{bmatrix}
40 & 50 & 40
\end{bmatrix}

相関係数$xx$を求める

Error_x =  \left\{ (80-50) + (20-50) + (50-50) \right\}
\\
cov_{xx} = \frac{1}{3} Error_x * Error_x^{T}=600
\\
std_{xx} = \sqrt{ \frac{1}{3} \left\{ (80-50)^{2} + (20-50)^{2} + (50-50)^{2} \right\}} = 24.495
\\
corr_{xx} = \frac{cov_{xx}}{std_{xx} * std_{xx}} =  \frac{600}{24.495 * 24.495} = 1

同様に$xy$～$zz$まで求める。

corr_{xy} = 0.971
corr_{xz} = -0.866
corr_{yz} = -0.961

よって、以下の行列が得られた。

corr_{mat}=\begin{bmatrix}
1 & 0.971 & -0.866 \\
0.971 & 1 & -0.961 \\
-0.866 & -0.961 & 1
\end{bmatrix}

コード

import numpy as np

A = np.array([
              [80, 20, 50], # math
              [100, 30, 80], # science
              [40, 50, 40] # lang
              ])

print(np.corrcoef(A))
print("---------")
idx = 0
idy = 0
num = 3
a_v = np.sqrt( 1/num * np.sum(np.power( (A[idx] - np.mean(A[idx])), 2 ) ) )
b_v = np.sqrt( 1/num * np.sum(np.power(  (A[idy] - np.mean(A[idy])), 2 ) ) )
a = (A[idx] - np.mean(A[idx]))
b = (A[idy] - np.mean(A[idy]))
cor = 1/num * (np.dot(a, b.T))
print(cor / (a_v * b_v))