本記事では、近接勾配法に関する数学的な基礎知識の一部をまとめます。
近接勾配法のアルゴリム自体は少ししか扱わないので、そちらを探される方は文献1,2,3などを参照して下さい。
Epigraph and Subgradient
$f$ のエピグラフ (epigraph) は
\begin{equation*}
\mathrm{epi}\ f \mathrel{\vcenter{:}}= \left\lbrace (y, t) \in \mathbb{R}^{n+1} \mathrel{\big|} f(y) \leq t \right\rbrace
\end{equation*}
と定義されます。
また、$f$ の点 $x_0 \in \mathrm{dom}\ f$ において、
\begin{equation*}
f(x) - f(x_0) \geq \langle v, x - x_0 \rangle \quad \text{for all } x \in \mathrm{dom}\ f
\end{equation*}
を満たす $v \in \mathbb{R}^n$ は $f$ の劣勾配 (subderivative, subgradient) と呼ばれ、その集合 $\partial f(x)$ は 劣微分 (subdifferential) と呼ばれます。

Convex Conjugate
凸とは限らない関数 $f\colon \mathbb{R}^n \to \mathbb{R} \cup \lbrace+\infty\rbrace$ に対し、凸共役(convex conjugate, Fenchel conjugate, Legendre--Fenchel transformation)$f^*\colon \mathbb{R}^n \to \mathbb{R} \cup \lbrace+\infty\rbrace$ は、次のように定義されます:
\begin{align*}
f^*(x) &\mathrel{\vcenter{:}}= \sup_{y \in \mathbb{R}^n} \left\lbrace \langle x, y \rangle - f(y) \right\rbrace\\
&= -\inf_{y \in \mathbb{R}^n} \left\lbrace f(y) - \langle x, y \rangle \right\rbrace
\end{align*}
(なお $f^*$ の値域は、単なる $\mathbb{R}^n$ というよりその代数的双対だと解釈するのが自然です。dualityの節を参照して下さい。)
下図のように $n=1$ の場合、$f$(赤線)に対する傾き $x$ の接線(青点線)の最小切片に $-1$ をかけたものが $f^*$ (緑線)です。図の右側で $y$ 軸が下向きなことに注意して下さい。

(文献4より引用)
この最小切片の話を一般化すると、法線ベクトルが $\begin{bmatrix} x \ -1 \end{bmatrix}$ で $y=(0,\dots,0)$ で $\alpha$ となる超平面 $(y,t)\in \mathbb{R}^{n+1}$ は
\begin{align*}
&\left\lbrace (y, t) \in \mathbb{R}^{n+1} \mathrel{\bigg|} \left\langle \begin{bmatrix} x \\ -1 \end{bmatrix}, \begin{bmatrix} y \\ t-\alpha \end{bmatrix} \right\rangle = 0 \right\rbrace\\
={}& \left\lbrace (y, t) \in \mathbb{R}^{n+1} \mathrel{\big|} \langle x, y \rangle + \alpha = t \right\rbrace
\end{align*}
であるので、
\begin{align*}
&f^*(x) \\
={}& \sup_{y \in \mathbb{R}^n} \left\lbrace \langle x, y \rangle - f(y) \right\rbrace\\
={}& \min\lbrace \alpha \in \mathbb{R} \mathrel{|} \langle x, y \rangle \leq f(y) + \alpha \text{ for all } y \in \mathbb{R}^n \rbrace \\
={}& -\max\lbrace \alpha \in \mathbb{R} \mathrel{|} \langle x, y \rangle + \alpha \leq f(y) \text{ for all } y \in \mathbb{R}^n \rbrace\\
={}& -\max\lbrace \alpha \in \mathbb{R} \mathrel{|} \text{ 上記を満たす $\mathrm{dom}\ f$ の支持超平面} \rbrace
\end{align*}
と支持超平面(青点線)を用いて同様の解釈ができます。
なお、次のKenjiro Sugimotoさんの記事には直感的に分かりやすい動画形式の説明もあります。
Fenchel--Moreau Theorem
上図では $f = f^{**}$ となっています。これはFenchel--Moreau theoremとして知られる結果です。
$f \colon \mathbb{R}^n \to \mathbb{R} \cup \lbrace+\infty\rbrace$ において、$f = f^{**}$ であることは、$f \equiv +\infty$ あるいは $f \equiv -\infty$ という例外を除き、$f$ が閉真凸関数であることと同値です。
Fenchel--Young Inequality
定義を踏まえると当然ですが、任意の $x \in \mathbb{R}^n$, $y \in \mathbb{R}^n$ に対し、
\langle x, y \rangle \leq f(y) + f^*(x)
が成立します。これはFenchel's inequality または Fenchel--Young inequalityと呼ばれます。
Infimal Convolution
続いて、極小畳み込み(infimal convolution)について述べます。
"infimal"とは下限のという意味を持つ英単語で、この概念に関する"Earliest(?) work"は1919年ともされています。
Infimal convolution は、次のように定義されます。
\begin{align*}
(f \mathrel{\square} g)(x) &\mathrel{\vcenter{:}}= \inf_{y \in \mathbb{R}^n} \left\lbrace f(y) + g(x - y) \right\rbrace\\
&= \inf_{x_1 + x_2 = x} \left\lbrace f(x_1) + g(x_2) \right\rbrace
\end{align*}

図は、$f$ (黒線) と $g=\frac{1}{2}\lVert \cdot \rVert_2^2$ のinfimal convolutionを示しています。各黒点が $(y,f(y))$ に対応しており、infimal convolutionでは $f(y)+g(x-y)$ (青点線) の $\inf$ を取ります。
また、文献5などでは、有限個の関数に対しても拡張されています。
更に、$f,g$ が共に真凸関数であっても、$f \mathrel{\square} g$ が真凸関数とは限りません。ぱっと見だと非自明ですが、$f,g$ が傾きの異なる線形関数の場合、$x \to \pm\infty$ で発散するので、$\inf$ が常に $-\infty$ になり、真凸関数とはなりません。
epi-sum
まず、前提として加法群の2つの部分集合 $A,B$ に対するミンコフスキー和 (Minkowski sum) $A \oplus B$ は、次のように定義されます。
A \oplus B \mathrel{\vcenter{:}}= \left\lbrace a + b \mathrel{|} a \in A, b \in B \right\rbrace
この前提のもとで上図を見ると、$f$ と $g$ の epigraph のMinkowski sum が $f \mathrel{\square} g$ の epigraph と一致、つまり、
\mathrm{epi}\ f \oplus \mathrm{epi}\ g = \mathrm{epi}\ (f \mathrel{\square} g)
がこの図では成立しています。
ただし、常に $\mathrm{epi}\ f \oplus \mathrm{epi}\ g = \mathrm{epi}\ (f \mathrel{\square} g)$ が成り立つ訳ではありません。以下に一般の場合を議論します。
$(x,t) = (x_f+x_g, t_f+t_g) \in \mathrm{epi}\ f \oplus \mathrm{epi}\ g$ に対し、
\begin{align*}
(f \mathrel{\square} g)(x) &= \inf_{x_1 + x_2 = x} \left\lbrace f(x_1) + g(x_2) \right\rbrace\\
&\leq f(x_f) + g(x_g)\\
&\leq t_f + t_g \quad (\because \mathrm{epi}\text{ の定義})\\
&= t
\end{align*}
なので、定義より $(x,t) \in \mathrm{epi}\ (f \mathrel{\square} g)$ が成り立ちます。つまり、$\mathrm{epi}\ f \oplus \mathrm{epi}\ g \subseteq \mathrm{epi}\ (f \mathrel{\square} g)$ が常に成り立ちます。
また、$(x,t) \in \mathrm{epi}\ (f \mathrel{\square} g)$ に対し、$(f \mathrel{\square} g)(x)$ を定義する下限が有限で達成される限り (文献6 Section 1.H Exercise 1.28)、
\begin{align*}
&(f \mathrel{\square} g)(x) \\
={}& \inf_{x_1 + x_2 = x} \left\lbrace f(x_1) + g(x_2) \right\rbrace\\
={}& f(x_1) + g(x_2) \quad (\text{この} x_1, x_2 \text{の存在が仮定内容})\\
\mathrel{\vcenter{:}}={}& t_1 + t_2 \quad (\text{このようにそれぞれ定義})\\
\leq{}& t \quad (\because \mathrm{epi}\ (f \mathrel{\square} g)\text{ の定義})
\end{align*}
となるので、$g(x_2) = t_2 \leq t-t_1$ となることから $(x_1,t_1) \in \mathrm{epi}\ f$ かつ $(x_2,t-t_1) \in \mathrm{epi}\ g$ となります。
以上より、$(x,t) = (x_1+x_2, t_1+(t-t_1)) \in \mathrm{epi}\ f \oplus \mathrm{epi}\ g$ が成り立ち、上記の条件を満たす場合には $\mathrm{epi}\ f \oplus \mathrm{epi}\ g = \mathrm{epi}\ (f \mathrel{\square} g)$ とこの関係は等号で成立します。
なお、厳密な意味でのepigraph、即ち、epigraphの定義における "$\leq$" を "$<$" に置き換えると、特段の仮定無しに
\begin{equation*}
\begin{split}
&\lbrace (x_1, t_1) \in \mathbb{R}^{n+1} \mathrel{|} f(x_1) < t_1 \rbrace \\
\oplus{}& \lbrace (x_2, t_2) \in \mathbb{R}^{n+1} \mathrel{|} g(x_2) < t_2 \rbrace\\
={}&\lbrace (x,t) \in \mathbb{R}^{n+1} \mathrel{|} (f \mathrel{\square} g)(x) < t \rbrace
\end{split}
\end{equation*}
は簡単に示せます。(文献6 Section 1.H Exercise 1.28, 文献7)
このことからinfimal convolution $f \mathrel{\square} g$ は epi-sum (epi-addition) とも呼ばれます。なお、epi-multiplication という操作も同じ文献などで記述されています。
Convex Conjugate に対する性質
文献8 Theorem 4.16 などで述べられている有名な性質として、proper な(凸とは限らない)関数 $f,g$ に対し、
(f \mathrel{\square} g)^* = f^* + g^*
が成立します。
\begin{align*}
&(f \mathrel{\square} g)^*(x)\\
={}& \sup_{y \in \mathbb{R}^n} \left\lbrace \langle x, y \rangle - (f \mathrel{\square} g)(y) \right\rbrace\\
={}& \sup_{y \in \mathbb{R}^n} \left\lbrace \langle x, y \rangle - \inf_{z \in \mathbb{R}^n} \left\lbrace f(z) + g(y - z) \right\rbrace \right\rbrace\\
={}& \sup_{y \in \mathbb{R}^n, z \in \mathbb{R}^n} \left\lbrace \langle x, y \rangle - \left( f(z) + g(y - z) \right) \right\rbrace\\
={}& \sup_{y \in \mathbb{R}^n, z \in \mathbb{R}^n} \left\lbrace \left(\langle x, z \rangle - f(z)\right) + \left( \langle x,y-z \rangle - g(y - z)\right) \right\rbrace\\
={}& \sup_{z \in \mathbb{R}^n} \left\lbrace \langle x, z \rangle - f(z) \right\rbrace + \sup_{y \in \mathbb{R}^n} \left\lbrace \langle x, y \rangle - g(y) \right\rbrace\\
={}& \left(f^* + g^*\right)(x)
\end{align*}
この等式の意味を $n=1$ で考えると、
- $(f \mathrel{\square} g)^* (x)$: $f$ と $g$ のepigraphのMinkowski和に対する接線の内、傾き $x$ で切片が最小のもの
- $(f^* + g^*)(x)$: $f$ のepigraphに対する接線の内、傾き $x$ で切片が最小のものと、$g$ のepigraphに対する接線の内、傾き $x$ で切片が最小のものの、和
が等しいということを主張しており、直感的には非常に自明です。
他にもいくつかの似たようなinfimal convolutionとconvex conjugateの関係が文献8に記述されています。
Huber Loss Function
Huber損失 (Huber loss function) は、成分毎に定義され、次のように表現されます。(参考)
\begin{equation*}
L_{\delta}(x) = \begin{cases}
\frac{1}{2} x^2 & \text{for } \lvert x \rvert \leq \delta, \\
\delta \cdot \left(\lvert x \rvert - \frac{1}{2} \delta\right) & \text{otherwise}.
\end{cases}
\end{equation*}
簡単のため $\delta = 1$ とすると、
\begin{equation*}
L_1(x) = \begin{cases}
\frac{1}{2} x^2 & \text{for } \lvert x \rvert \leq 1, \\
\lvert x \rvert - \frac{1}{2} & \text{otherwise}.
\end{cases}
\end{equation*}
となり、下図のオレンジ線のようになります。

図から明らかなように、Huber loss function は、$\lVert \cdot \rVert_1$ と $\frac{1}{2} \lVert \cdot \rVert_2^2$ の infimal convolution として表現できます。
\begin{align*}
&\left(\lVert \cdot \rVert_1 \mathrel{\square} \frac{1}{2} \lVert \cdot \rVert_2^2\right)(x)\\
={}& \inf_{y \in \mathbb{R}^n} \left\lbrace \lVert y \rVert_1 + \frac{1}{2} \lVert x - y \rVert_2^2 \right\rbrace\\
={}& \sum_{i=1}^n \inf_{y_i \in \mathbb{R}} \left\lbrace \lvert y_i \rvert + \frac{1}{2} (x_i - y_i)^2 \right\rbrace \\
={}& \sum_{i=1}^n L_1(x_i)
\end{align*}
となります。
最後の等式の導出を以下にします。まず、
\begin{align*}
& \lvert y \rvert + \frac{1}{2} (x - y)^2 \\
={} &\begin{cases}
+y+ \frac{1}{2} (x - y)^2 & \text{for } y \geq 0, \\
-y + \frac{1}{2} (x - y)^2 & \text{for } y < 0
\end{cases}
\end{align*}
であり、この最小値は
\begin{equation*}
\begin{cases}
+x-\frac{1}{2} \quad (y=x-1)& \text{for } 1 \leq x, \\
\frac{1}{2} x^2 \quad\quad\;\; (y=0) & \text{for } -1 < x < 1, \\
-x-\frac{1}{2} \quad (y=x+1) & \text{for } x \leq -1
\end{cases}
\end{equation*}
です。これは $L_1(x)$ と一致するので、結局、
\inf_{y \in \mathbb{R}} \left\lbrace \lvert y \rvert + \frac{1}{2} (x - y)^2 \right\rbrace = L_1(x)
です。
なお、これら最小値を達成するときの $y$ を表す関数
\begin{equation*}
S(x) \mathrel{\vcenter{:}}=
\begin{cases}
x-1 & \text{for } 1 \leq x, \\
0 & \text{for } -1 < x < 1, \\
x+1 & \text{for } x \leq -1
\end{cases}
\end{equation*}
は、Soft Thresholding Operator と呼ばれます。
また、「成分毎に定義」と書いたように、2次元の場合も定義できて、下図のようになります。

Proximal Operator
$f\colon \mathbb{R}^n \to \mathbb{R} \cup \lbrace+\infty\rbrace$ を閉真凸関数とします。近接写像 (proximal operator) (参考1,2)は、次のように定義されます。
\mathrm{prox}_{f}(v) \mathrel{\vcenter{:}}= \arg\min_{x \in \mathrm{R}^n} \left\lbrace f(x) + \frac{1}{2} \lVert x - v \rVert_2^2 \right\rbrace
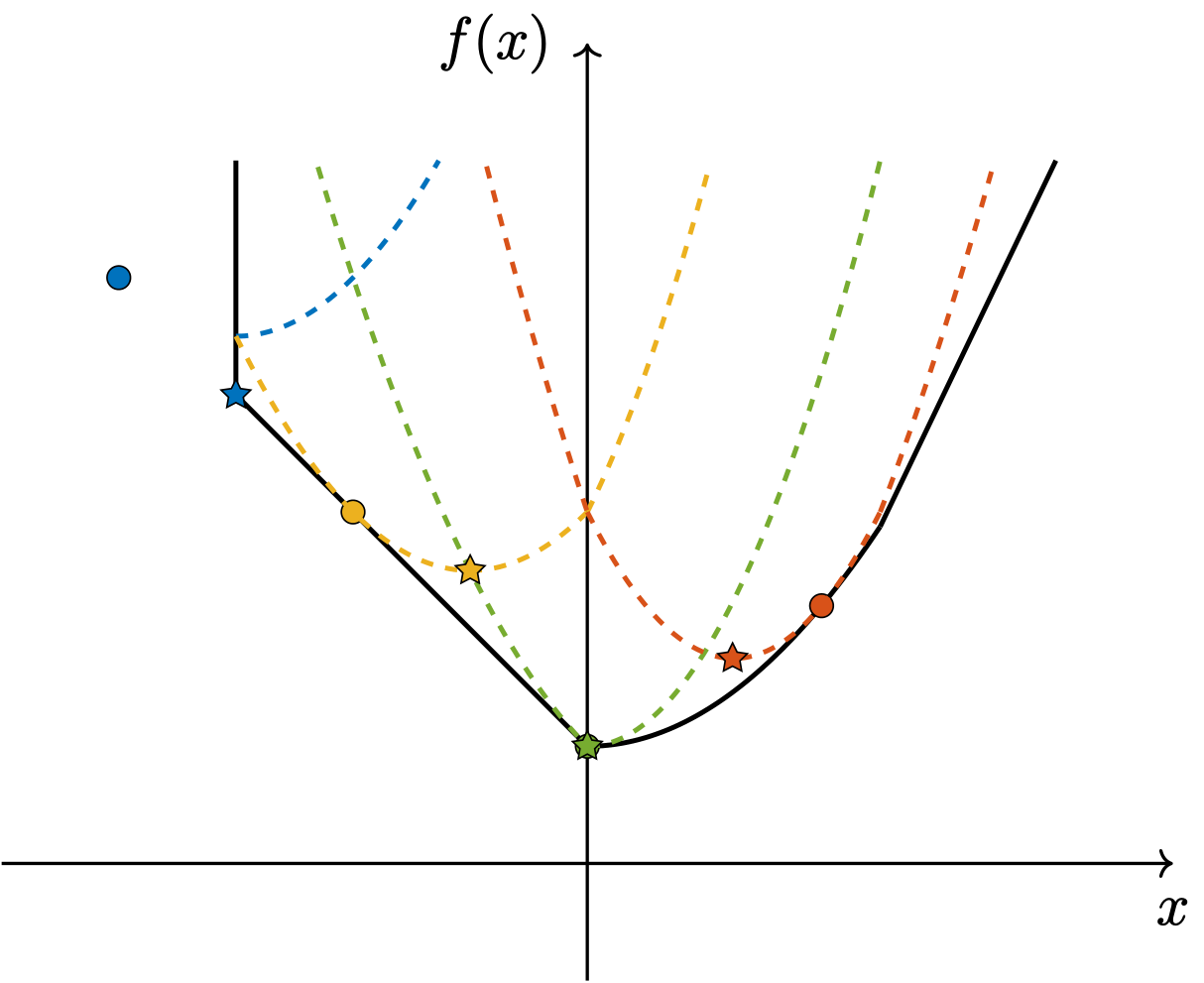
この図では、各色の丸点が $(v,f(v))$ を、その色の点線が $f(x)+\frac{1}{2}\lVert x-v \rVert_2^2$ を示しています。青色の点の $f(v)$ は $+\infty$ であるので、例外的に適当な位置にあります。
proximal operator は、点線における最小解である星印の位置を返します。特に、青色のように $\mathrm{dom}\ f$ の外側にある場合には大まかに射影演算子のように振る舞い、それ以外の場合には大まかに降下方向に進ませるような演算子として振る舞うことを確認してください。
Well-Definedness の証明
これが well-defined である ($\mathrm{prox}_f(v)$ が単集合(singleton)である) ことは次のように示されます。(文献8 Theorem 6.3 および文献8 Theorem 5.25に厳密な証明があります)
$\mathrm{prox}_f(v)$ の定義より、
f(x)+ \frac{1}{2} \lVert x - v \rVert_2^2
が、唯一の最小解を持つことを示せば良いです。
$f(x)$ が閉真凸関数であることから、この関数は閉真強凸関数です。故に、閉真強凸関数が唯一の最小解を持つことを示せば良いです。
真凸性より、ある $r$ が存在して level set $\lbrace x \mathrel{\mid} f(x) \leq r\rbrace$ は非空となります。閉性よりこれは閉集合で、強凸性より有界集合です。よって、ボルツァーノ゠ワイエルシュトラスの定理から、この level set は非空なコンパクト集合です。
また、この関数は閉真凸関数であるので下半連続で、半連続関数へ拡張された最大値最小値定理 (別途参照) から最小値および最小解を持ちます。最小解が唯一なのは強凸性より自明です。
以上より、この関数は唯一の最小値を持ち、$\mathrm{prox}_{f}(v)$ は well-defined です。
この証明で、それぞれの仮定が何の為にあるのか、ということを1次元の場合で考えると、
- $f$ が閉でないと、$x<0$ で $+\infty$, $x=0$ で $1$, $x>0$ で $\frac{1}{2}x^2$ という関数
- $f$ が真(凸)でないと、$f(x)=+\infty$ という定数関数
- $f$ が凸でないと、$f(x)=-x^2$ という関数
- $f+\frac{1}{2}\lvert \cdot \rvert_2^2$ が強凸でないと、$(f+\frac{1}{2}\lvert \cdot \rvert_2^2)(x)=1/x \ (x>0)$ のように単調減少していて level set が非有界な関数
がそれぞれ最小値を持たず反例となります。
なお、$\mathrm{dom}\ f = \mathbb{R}^n$ である場合は、Wikiにあるようにもっと自明です。
Proximal Operator の直感的な理解
$f$ に定数倍のパラメータ $\lambda$ を掛けたものに対する proximal operator は、
\begin{align*}
&\mathrm{prox}_{\lambda f}(v) \\
={}& \arg\min_{x \in \mathbb{R}^n} \left\lbrace \lambda f(x) + \frac{1}{2} \lVert x - v \rVert_2^2 \right\rbrace \\
={}&\arg\min_{x \in \mathbb{R}^n} \left\lbrace f(x) + \frac{1}{2\lambda} \lVert x - v \rVert_2^2 \right\rbrace
\end{align*}
です。
この時、$\lambda \to \infty$ では、
\begin{equation*}
\mathrm{prox}_{\lambda f}(v) \to \arg\min_{x \in \mathbb{R}^n} f(x)
\end{equation*}
と、$f$ の最小解に近づきます。一方、$\lambda \to 0$ では、
\begin{align*}
&\mathrm{prox}_{\lambda f}(v) \\
\to{}& \begin{cases}
v & \text{for } x \in \mathrm{dom}\ f \\
\arg\min_{x \in \mathrm{dom}\ f} \lVert x-v \rVert_2 & \text{otherwise}
\end{cases}
\end{align*}
と射影演算子の振る舞いを示します。
このことから、proximal operator はこれらの中間的な操作だと解釈できます。

(文献9より引用)
Proximal Operator での劣勾配
また、$p_v = \mathrm{prox}_{\lambda f}(v)$ とすると、次の性質が成り立ちます。
\begin{align*}
&p_v = \arg\min_{x \in \mathbb{R}^n} \left\lbrace f(x) + \frac{1}{2\lambda} \lVert x - v \rVert_2^2 \right\rbrace\\
\iff{}& 0 \in \partial f(p_v) + \frac{1}{\lambda} (p_v - v) \quad (\because \text{凸性})\\
\iff{}& \frac{1}{\lambda} (v - p_v) \in \partial f(p_v)
\end{align*}
ここで、
\begin{equation*}
p_y \mathrel{\vcenter{:}}= \mathrm{prox}_{\lambda f}(y), \quad p_x \mathrel{\vcenter{:}}= \mathrm{prox}_{\lambda f}(x)
\end{equation*}
とすると、本記事冒頭で述べたように、
\begin{equation*}
f(p_y) - f(p_x) \geq \left\langle \frac{1}{\lambda} (x - p_x), p_y - p_x \right\rangle
\end{equation*}
が成立します。
Firm Nonexpansiveness
Proximal operator は、firm nonexpansiveness と呼ばれる次の性質を持ちます(参考1, 2, 3):
\begin{equation*}
\lVert p_y - p_x \rVert_2^2 \leq \langle y - x, p_y - p_x \rangle
\end{equation*}

$n=1$ の場合を上に再掲しました。これは $y>x$ に対して $p_y - p_x \leq y-x$、つまり、☆間の距離は○間の距離より短いことを示しており、全体が縮小写像のようになっていることに対応します。
Firm nonexpansiveness の証明をします。Proximal Operatorでの劣勾配で示したように、
\begin{align*}
f(p_y) - f(p_x) &\geq \left\langle \frac{1}{\lambda} (x - p_x), p_y - p_x \right\rangle \\
f(p_x) - f(p_y) &\geq \left\langle \frac{1}{\lambda} (y - p_y), p_x - p_y \right\rangle
\end{align*}
であるので、両辺を足して
\begin{align*}
&0 \geq \frac{1}{\lambda} \langle x-p_x-y+p_y, p_y - p_x \rangle\\
\iff&0 \geq \lVert p_y - p_x \rVert_2^2 - \langle y - x, p_y - p_x \rangle\\
\iff& \lVert p_y - p_x \rVert_2^2 \leq \langle y - x, p_y - p_x \rangle
\end{align*}
が成立します。
なお、この結果は Kachurovskiiの定理の劣勾配版として解釈できます。特に、このような性質を持つ写像は monotone mapping とも呼ばれるようです。
Moreau Envelope
続いて、Moreau envelope について述べます。
Jean-Jacques Moreauはフランスの数学者で、「モロー」と読むのが一般的と思われます。Envelopeは封筒などの意味が有名ですが、包絡線の意味もあります。
下半連続な真凸関数 $f\colon \mathbb{R}^n \to \mathbb{R} \cup \lbrace+\infty\rbrace$ に対して、Moreau envelope (Moreau--Yoshida regularization) は次のように定義されます(参考):
M_{\lambda f}(v) \mathrel{\vcenter{:}}= \inf_{u \in \mathbb{R}^n} \left\lbrace f(u) + \frac{1}{2\lambda} \lVert u - v \rVert^2 \right\rbrace
ところで、この定義の $\inf$ は $\min$ に変えても問題ありませんが、Moreau envelopeは下半連続な真凸 (つまり、閉真凸) 関数以外にも定義されることがあるので、$\inf$ とされているものと思われます。
(Proximal operatorで $\arg\min$ が使われている為、私は混乱しました。文献によってもこの辺りは $\min$ を使うか $\inf$ を使うか揺れているようです。)

(文献10より引用)
Infimal Convolution との関係
Moreau envelope $M_{\lambda f}$ は、$\lambda f$ と $\frac{1}{2} \lVert \cdot \rVert_2^2$ の infimal convolution として表現できます。
実際、
\begin{align*}
&\left(\lambda f \mathrel{\square} \frac{1}{2} \lVert \cdot \rVert_2^2 \right)(x) \\
={} & \inf_{y \in \mathbb{R}^n} \left\lbrace \lambda f(y) + \frac{1}{2} \lVert x - y \rVert^2 \right\rbrace \\
={} & \inf_{y \in \mathbb{R}^n} \left\lbrace f(y) + \frac{1}{2\lambda} \lVert x - y \rVert^2 \right\rbrace
\end{align*}
です。
Moreau Envelope の勾配
下半連続な真凸関数 $f$ に対して、Moreau envelope $M_{\lambda f}$ の勾配は、次のように表現できます。
\begin{align*}
& \nabla M_{\lambda f}(v) \\
={}& \frac{1}{\lambda} (x- \mathrm{prox}_{\lambda f}(x))\\
={}& \frac{1}{\lambda} \left(x - \inf_{u \in \mathbb{R}^n} \left\lbrace f(u) + \frac{1}{2\lambda} \lVert u - v \rVert^2 \right\rbrace\right)
\end{align*}
このことを以下に導出します。
導出
こちらの講義資料を参考に、フレシェ微分可能であることを示し、$M_{\lambda f}$ の勾配を導きます。
やや天下り的ですが、この証明では
\begin{equation*}
\lim_{y \to x} \frac{M_{\lambda f}(y) - M_{\lambda f}(x) - \left\langle y-x, \frac{1}{\lambda} (x-\mathrm{prox}_{\lambda f}(x)) \right\rangle}{\lVert y - x \rVert} = 0
\end{equation*}
を示します。これはフレシェ微分の定義そのものの形式であり、一般に勾配はフレシェ導関数と一致するので、
\nabla M_{\lambda f}(x) = \frac{1}{\lambda} (x-\mathrm{prox}_{\lambda f}(x))
が結果として導かれます。
では、極限値が $0$ であることを示します。まず、
\begin{align*}
p_y &\mathrel{\vcenter{:}}= \mathrm{prox}_{\lambda f}(y) = \arg\min_{u \in \mathbb{R}^n} \left\lbrace f(u) + \frac{1}{2\lambda} \lVert u - y \rVert^2 \right\rbrace, \\
p_x &\mathrel{\vcenter{:}}= \mathrm{prox}_{\lambda f}(x) = \arg\min_{u \in \mathbb{R}^n} \left\lbrace f(u) + \frac{1}{2\lambda} \lVert u - x \rVert^2 \right\rbrace
\end{align*}
とおくと、
\begin{align*}
& M_{\lambda f}(y) - M_{\lambda f}(x) \\
={}& \inf_{u \in \mathbb{R}^n} \left\lbrace f(u) + \frac{1}{2\lambda} \lVert u - y \rVert^2 \right\rbrace - \inf_{u \in \mathbb{R}^n} \left\lbrace f(u) + \frac{1}{2\lambda} \lVert u - x \rVert^2 \right\rbrace\\
={}& f(p_y)+\frac{1}{2\lambda} \lVert p_y - y \rVert^2 - f(p_x) - \frac{1}{2\lambda} \lVert p_x - x \rVert^2 \\
\geq{}& \left\langle p_y - p_x, \frac{1}{\lambda} (x - p_x) \right\rangle + \frac{1}{2\lambda} \lVert p_y - y \rVert^2 - \frac{1}{2\lambda} \lVert p_x - x \rVert^2 \\
={}& \frac{1}{2\lambda} \left(\lVert (p_y - y) - (p_x - x) \rVert^2 + 2 \langle y-x, x-p_x \rangle \right)\\
\geq{}& \frac{1}{\lambda} \langle y-x, x-p_x \rangle
\end{align*}
となります。最初の不等式はProximal Operatorで示した式です。その次の等式変形は非自明ですが、地道に展開整理すると導けます。この不等式より極限値が $0$ 以上であることは直ちに従います。
次に、極限値が $0$ 以下であることを示します。上記不等式で $x,y$ を入れ替えると、
\begin{align*}
&M_{\lambda f}(x) - M_{\lambda f}(y) \geq \frac{1}{\lambda} \langle x-y, y-p_y \rangle\\
\iff&M_{\lambda f}(y) - M_{\lambda f}(x) \leq \frac{1}{\lambda} \langle y-x, y-p_y \rangle
\end{align*}
となります。よって、
\begin{align*}
& M_{\lambda f}(y) - M_{\lambda f}(x) - \frac{1}{\lambda} \langle y-x, x-p_x \rangle\\
\leq {}& \frac{1}{\lambda} \langle y-x, y - p_y - x + p_x \rangle \\
= {}& \frac{1}{\lambda} \lVert y - x \rVert^2 - \frac{1}{\lambda} \langle y-x, p_y - p_x \rangle \\
\leq {}& \frac{1}{\lambda} \lVert y - x \rVert^2 \quad (\because \text{Firm Nonexpansiveness})
\end{align*}
です。最後の不等式は、Firm Nonexpansivenessで示した事実より、内積 $\langle y-x, p_y - p_x \rangle$ が非負であることを用いています。
以上より、勾配が導出されました。
Proximal Gradient Method
近接勾配法(Proximal Gradient Method)と、それに関連する諸定義を少しだけ記述します。文献8 Chapter 10で紹介されている内容です。
Proximal Gradient Method の更新則
まず、以下のcomposite minimization problem を考えます。
\begin{equation*}
\min_{x \in \mathbb{R}^n} \left\lbrace f(x) + g(x) \right\rbrace
\end{equation*}
ただし、
- $g \colon \mathbb{R}^n \to (-\infty, +\infty]$ は閉真凸関数
- $f \colon \mathbb{R}^n \to (-\infty, +\infty]$ は閉真関数かつ、$\mathrm{dom}\ f$ が凸集合で、$\mathrm{dom}\ g \subseteq \mathrm{int}(\mathrm{dom}\ f)$ を満たす
- $f$ はリプシッツ連続である
とします。
ここで、この問題を解く為に生成する点列を考えます。$x^k$ を現在の点、$t_k$ を正の定数として、次のように更新則を定義します。
x^{k+1} = \arg\min_{x \in \mathbb{R}^n} \left\lbrace f(x^k) + \left\langle \nabla f(x^k), x - x^k \right\rangle + g(x) + \frac{1}{2t_k} \lVert x - x^k \rVert^2 \right\rbrace
右辺の中身に注目すると、
- $f(x^k)+ \left\langle \nabla f(x^k), x - x^k \right\rangle$ は $f$ の線形近似です。
- $g(x)$ は そのまま持ってきただけです。
- 最後の $\frac{1}{2t_k} \lVert x - x^k \rVert^2$ は、$x^k$ からの距離を小さくするような働きを持ち、近接項(prox term)と呼ばれます。一種の正則化項です。
一階微分の情報を基にこのような部分問題を考えるのは、かなり自然な発想です。
近接勾配法 (proximal gradient method) とは一般に、初期点 $x^0 \in \mathrm{int}(\mathrm{dom}\ f)$ を与え、$k=0,1,\ldots$ に対して、上記の更新則で最適化していく手法のことを指します。直線探索と組合せることも勿論可能です。
Prox-Grad Operator
ここで、$x^{k+1}$ は次のように表現できます。
\begin{align*}
x^{k+1} &= \arg\min_{x \in \mathbb{R}^n} \left\lbrace t_k g(x) + \frac{1}{2} \lVert x - (x^k - t_k \nabla f(x^k)) \rVert^2 \right\rbrace \\
&= \mathrm{prox}_{t_k g}\left(x^k - t_k \nabla f(x^k)\right)
\end{align*}
ここに、近接写像である $\mathrm{prox}_{t_k g}$ が出てきました。
これを踏まえると、確かに近接項・近接勾配法・近接写像はそれぞれ深い関係にあることがよく分かります。
また、一般に、
T_L^{f,g} (x) \mathrel{\vcenter{:}}= \mathrm{prox}_{\frac{1}{L} g}\left(x - \frac{1}{L} \nabla f(x)\right)
と定義することで、$L_k = 1/t_k$ とすると、近接勾配法の更新則は
x^{k+1} = T_{L_k}^{f,g}(x^k)
とも簡潔に表現できます。この $T_L^{f,g}$ は、prox-grad operator と呼ばれます。
Gradient Mapping
この $T_L^{f,g}$ を用いると、次の gradient mapping $\mathcal{G}_L^{f,g} \colon \mathrm{int}(\mathrm{dom}\ f) \to \mathbb{R}^n$ を定義できます。
\mathcal{G}_L^{f,g}(x) \mathrel{\vcenter{:}}= L \left(x - T_L^{f,g}(x)\right)
先程の話と合わせると、
\begin{align*}
x^{k+1} &= \mathrm{prox}_{t_k g}\left(x^k - t_k \nabla f(x^k)\right) \\
&= T_{L_k}^{f,g}(x^k) \\
&= x^k - \frac{1}{L_k} \mathcal{G}_{L_k}^{f,g}(x^k)
\end{align*}
となっており、一般の最急降下法では $x^{k+1} = x^k - \frac{1}{L_k} \nabla f(x^k)$ であることを踏まえると、このgradient mapping は、通常の勾配演算子 $\nabla f(x^k)$ の一般化に対応していると見做せます。
実際、$g(x)=0$ の場合、
\begin{align*}
\mathcal{G}_L^{f,0}(x) &= L \left(x - T_L^{f,0}(x)\right) \\
&= L \left(x - \left(x - \frac{1}{L} \nabla f(x)\right)\right) \\
&= \nabla f(x)
\end{align*}
なので、勾配に一致します。
1次元の場合の図も示しておきます。$T_L^{f,g}$ が次の点 $x^{k+1}$ に、$\mathcal{G}_L^{f,g}$ が勾配の一般化にそれぞれ対応していることが見て取れるかと思います。

余談ですが、このGradient Mappingは Zhu, H. (2025). An Inexact Proximal Newton Method for Nonconvex Composite Minimization. Journal of Scientific Computing, 102(3), 79. という最近の論文の理論解析でも用いられています。すごい!
そして更なる余談として、私が2か月間くらいやっていた研究は、この論文により完全に破壊されました、悲しい!Moreau's Decomposition
Moreau's Decomposition について述べます。 (この論文にも詳しく載っているようです)
Conjugate Subgradient Theorem
あとの証明で使うため、先に以下の定理を示します(文献8 Theorem 4.20)。
$f\colon \mathbb{R}^n \to \mathbb{R} \cup \lbrace+\infty\rbrace$ を真凸関数とする。任意の $x \in \mathbb{R}^n$, $y \in \mathbb{R}^n$ に対して、次は同値である:
- $\langle x, y \rangle = f(x) + f^*(y)$
- $y \in \partial f(x)$
- $x \in \partial f^*(y)$ (ただし、$f$ はさらに閉であるとする)
証明は以下の通りです。$y \in \partial f(x)$ であることは
\begin{align*}
& f(z) \geq f(x) + \langle y, z - x \rangle\\
\iff {}& \langle y, x \rangle - f(x) \geq \langle y, z \rangle - f(z) \quad \forall z \in \mathbb{R}^n
\end{align*}
が成り立つことと同値で、$z$ について $\sup$ を取ると定義より、
\langle y, x \rangle - f(x) \geq f^*(y)
と同値です。記事序盤で触れたFenchel--Young Inequalityより
\langle y, x \rangle - f(x) \leq f^*(y)
であり、これは $\langle x, y \rangle = f(x) + f^*(y)$ と同値になります。
さらに $f$ が閉であると仮定すると、記事序盤で触れたFenchel--Moreau Theoremより $f^{**} = f$ であり、特に
\begin{align*}
& y \in \partial f(x) \\
\iff {}& \langle y, x \rangle = f(x) + f^*(y) \\
\iff {}& \langle x, y \rangle = (f^*)(y) + (f^*)^*(x)\\
\iff {}& x \in \partial f^*(y)
\end{align*}
となって、定理の主張が示されます。
Moreau's Decomposition Theorem
Moreau's Decomposition とは、一般に次のような分解を指します(文献8 Theorem 6.44)。
$f \colon \mathbb{R}^n \to \mathbb{R} \cup \lbrace+\infty\rbrace$ が閉真凸関数であるとき、任意の $x \in \mathbb{R}^n$ に対して、
\begin{equation*}
x = \mathrm{prox}_{f}(x) + \mathrm{prox}_{f^*}(x)
\end{equation*}
証明は以下の通りです。Proximal Operatorでの劣勾配で述べたように、$u=\mathrm{prox}_{f}(x)$ とすると、
\begin{equation*}
x-u \in \partial f(u)
\end{equation*}
が成立します。 直前で示したConjugate Subgradient Theoremより、
\begin{equation*}
u \in \partial f^*(x-u)
\end{equation*}
と同値です。これは整理すると、
\begin{align*}
& x-(x-u) \in \partial f^*(x-u) \\
\iff {}& x-u = \mathrm{prox}_{f^*}(x) \quad (\because \text{先程と同様の関係式}) \\
\iff {}& x = \mathrm{prox}_{f}(x) + \mathrm{prox}_{f^*}(x)
\end{align*}
となり、主張が示されます。
錐 $\mathcal{K}$ に対する指示関数 $f$ を考えると、
- $\mathrm{prox}_{f}(x)$ は $\mathcal{K}$ の射影演算子に対応
- $\mathrm{prox}_{f^*}(x^*)$ は極錐 $\mathcal{K}^0$ の射影演算子に対応
するので、分解は下図のように直感的理解が可能です。
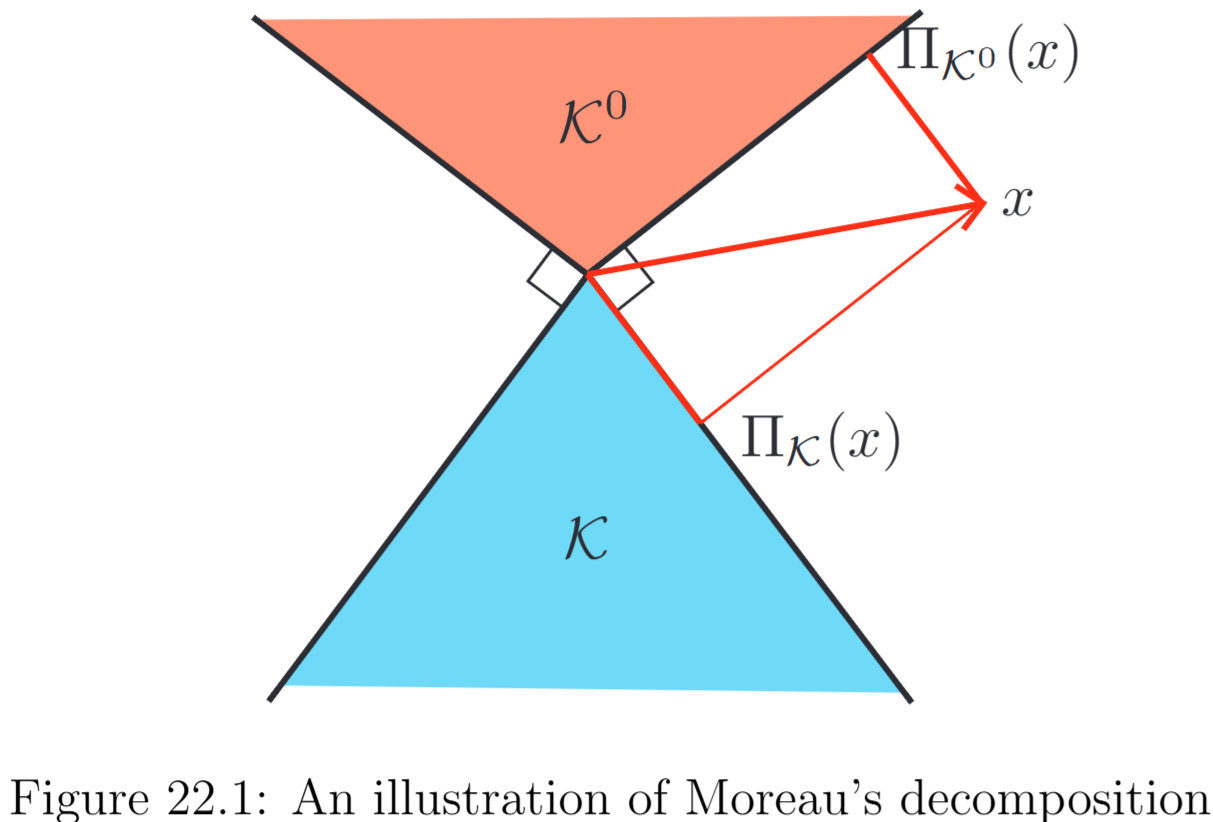
図の引用: リンク
Duality
Appendixとして、少し近接勾配法と関連が薄い話もありますが、双対を取り上げます。
代数的双対
初めに代数的双対(文献11 Definition 3.110)を取り上げます。
ざっくりとした説明としては、線形汎関数は $\phi_a(v)=\langle v, a \rangle$ のことを指し、この $\phi_a$ 全体が $V (\ni v)$ の代数的双対空間 $V^*$ を構成します。
線形汎関数 (linear functional) は、線形空間 $V$ から体 $F$(本記事では $\mathbb{R}$ または $\mathbb{C}$ とする)への線形写像と定義されます。体 $F$ 上の線形空間 $V$ の代数的双対空間 (algebraic dual space) $V^*$ は $V$ 上の線形汎関数 $\phi \colon V \to F$ 全体の成す集合 $\mathcal{L}(V,F)$ です。
$F$ が体であることから、
\begin{align*}
\begin{cases}
(\phi+\psi)(v) &\mathrel{\vcenter{:}}= \phi(v) + \psi(v)\\
(a \phi)(v) &\mathrel{\vcenter{:}}= a \phi(v)
\end{cases}
\\
(\phi \in V^*, \ \psi \in V^*, \ v \in V, \ a \in F)
\end{align*}
がそれぞれ定義できるので、$V^*$ も線形空間となります。
具体例として、二乗総和可能な無限複素数列の集合 $\ell^2$
\begin{equation*}
\ell^2 \mathrel{\vcenter{:}}= \left\lbrace (x_n)_{n=1}^{\infty} \mathrel{|} \sum_{n=1}^{\infty} \lvert x_n \rvert^2 < \infty \right\rbrace
\end{equation*}
を $V$ として考えます。なお、$\ell^2$ は数列空間と呼ばれ、線形空間となります。
$\ell^2$ 上の線形汎関数 $\phi \in V^* = \mathcal{L}(\ell^2,\mathbb{C})$ は、$e_n \mathrel{\vcenter{:}}= (0,\ldots,1,\ldots,0)$ を標準基底として
\begin{align*}
\phi(x) &= \phi((x_1, x_2, x_3, \ldots))\quad (\text{成分表示}) \\
&= \sum_{n=1}^{\infty} x_n \phi(e_n) \quad (\text{線形性}) \\
&= \sum_{n=1}^{\infty} x_n a_n \quad (a_n \mathrel{\vcenter{:}}= \phi(e_n))
\end{align*}
と $(a_n)_{n=1}^{\infty}$ で定まります。
また、(二乗総和可能などとは関係なく)任意の $(a_n)_{n=1}^{\infty}$ で線形汎関数を構築できるので、$V=\ell^2$ の代数的双対空間は $V^* \cong \ell^{\infty}$(複素数列全体)となります。
ここで、上記数式の最終行は内積として解釈できますが、実際、$V$ と $V^*$ は双対対と呼ばれる関係にあり、これにより標準内積(双線形形式)が定まります。
有限次元に慣れていると、$\langle x,a \rangle$ が $\phi_a(x) \mathrel{\vcenter{:}}= (\langle \cdot, a \rangle)(x)$ であるなどとはあまり意識しませんが、この辺の話が Fenchel双対の前提になります。
連続的双対
連続的双対(文献11 Section 7.A)についても軽く取り上げます。
位相線形空間 $V$ の連続的双対空間 (continuous dual space, topological dual space) は、その係数体 $F$ (本記事では $\mathbb{R}$ または $\mathbb{C}$ とする)への連続線形汎関数 $\phi\colon V \to F$ 全体の集合であり、$V'$ と書きます。連続という条件が加わるので、$V' \subseteq V^*$ です。
同じく二乗総和可能な無限複素数列の集合 $\ell^2$
\begin{equation*}
\ell^2 \mathrel{\vcenter{:}}= \left\lbrace (x_n)_{n=1}^{\infty} \mathrel{\Bigl|} \sum_{n=1}^{\infty} \lvert x_n \rvert^2 < \infty \right\rbrace
\end{equation*}
を $V$ として考えます。
$\ell^2$ は体 $\mathbb{C}$ 上の線形空間で $\lVert (x_n) \rVert_2 \mathrel{\vcenter{:}}= \sqrt{\sum_{n=1}^{\infty} \lvert x_n \rvert^2}$ というノルムが定義されており、特に位相線形空間となります。
ここで、連続線形汎関数 $\phi$ が一体どのような形で書けるのか? という問いに対する答えは非自明です。今回は、$\ell^2$ がヒルベルト空間(完備な内積空間)であることを踏まえると、Rieszの表現定理により、$V' \cong V$ となることが分かります。
Rieszの表現定理の主張内容は、ヒルベルト空間 $V$ と、任意の $\phi \in V^*$ に対し、ある $y \in V$ が一意的に存在して、
\begin{equation*}
\phi(x) = \langle x, y \rangle, \quad x \in V
\end{equation*}
とできるということであり、即ち $V \cong V^*$ を意味します。
(なお、$\ell^2$ は $\ell^p$ 空間の内ヒルベルト空間であるような唯一の空間であり、また $\mathbb{R}^n$ はヒルベルト空間なので、$(\mathbb{R}^n)' \cong \mathbb{R}^n$ です。)
この $X$ がさらにノルム線形空間である場合には、$X$ の双対空間にもノルムが
\begin{equation*}
\lVert \phi \rVert = \sup_{\lVert x \rVert \leq 1} \lvert \phi(x) \rvert
\end{equation*}
で定まります。これは双対ノルム (dual norm)と呼ばれ、連続的双対空間はそのような場面で最適化文脈でも登場します。
(連続的双対については以上です)
凸共役
上記を前提とすると、凸共役の話がほんの少し深く理解できて面白いです。
Wikiでは、次のような記述がされています。

ここで、定義に代数的双対空間 $X^*$ が登場しています。
本記事では凸共役において、$X$ も $X^*$ も $\mathbb{R}^n$ として表記していました。しかし、後者の意味する内容は、単にその元であるというよりも、寧ろ線形汎関数であって、文献12でもこの違いは明確に区別されるなど、理解に重要な点となります。
その他の双対
最も記したかった双対の話は以上で終わりですが、「双対」には、他にも様々あります。List of dualities では、70種以上の双対が挙げられており(平面グラフの双対、全称記号と存在記号の双対など)、その内のいくつかは上記のような最適化と近い話題も多いです。
例えば関連する話題としては、
-
ルジャンドル変換
- 解析力学や熱力学でおなじみ
- 凸共役の特殊な場合に相当 (あるいは、ルジャンドル変換の一般化が凸共役)
- 微分を用いた表現も有名
- Lagrange Duality
-
Fenchel Duality
- Fenchel's Duality Theorem とも
- 文献8 Theorem4.15、文献13 Theorem 31.1 など
- 分かりやすい1次元の場合の図解
- Wolfe Duality
などがあります。
Acknowledgement
本記事は修士課程における勉強目的で作成しており、指導教員の方々に感謝申し上げます。
-
Yamagen, Sakam. (2018). 近接勾配法とproximal operator. 甲斐性なしのブログ. ↩
-
Masashi, Sekino. (2018). 近接勾配法(Proximal Gradient Method). Qiita. ↩
-
Ochs, P. (2015). Long term motion analysis for object level grouping and nonsmooth optimization methods (Doctoral dissertation, PhD thesis, Albert-Ludwigs-Universität Freiburg). ↩
-
Ioffe, A. D., & Tihomirov, V. M. (2009). Theory of Extremal Problems: Theory of Extremal Problems. Elsevier. ↩
-
Rockafellar, R. T., & Wets, R. J. B. (2009). Variational analysis (Vol. 317). Springer Science & Business Media. ↩ ↩2
-
Bauschke, H. H., Goebel, R., Lucet, Y., & Wang, X. (2008). The proximal average: basic theory. SIAM Journal on Optimization, 19(2), 766-785. ↩
-
Beck, A. (2017). First-order methods in optimization. Society for Industrial and Applied Mathematics. ↩ ↩2 ↩3 ↩4 ↩5 ↩6 ↩7 ↩8
-
Nagahara, M. (2020). Algorithms for convex optimization. In Security risk management for the Internet of Things: Technologies and techniques for IoT security, privacy and data protection (Chapter 4). ↩
-
Tibshirani, R. J., Fung, S. W., Heaton, H., & Osher, S. (2024). Laplace Meets Moreau: Smooth Approximation to Infimal Convolutions Using Laplace's Method. arXiv preprint arXiv:2406.02003. ↩
-
Nesterov, Y. (2018). Lectures on convex optimization (Vol. 137, pp. 5-9). Berlin: Springer. ↩
-
Rockafellar, R. T. (1970). Convex analysis. Princeton university press. ↩