AHC030の没解法について

Last updated at 2024-02-20Posted at 2024-02-20

AHC030の没解法について

はじめに

2024年2月9日から14日にかけて開催されたTHIRD プログラミングコンテスト2023（AtCoder Heuristic Contest 030）に参加し、暫定6位・最終8位になりました。

私の解法自体は以下のツイートに大まかにまとめてあります。

ただ、この解法は1位のterry_u16さんやWriterであるwata_adminさんの解法の完全下位互換に過ぎないので、本記事で触れることはありません。もしこの解法にご興味がある方は、wataさんの提出や、東邦大学メディアネットセンターのページなどを参照して頂ければと思います。

ところで、私はこのコンテストにおいて最終的に提出した解法以外にも、とある解法を試していました。結果自体は（その方針単体だと）かなり悪いものではありましたが、個人的に面白く、似たような解法の方もお見かけしたのでここに記します。

解法の概略

解法の概略を述べます。

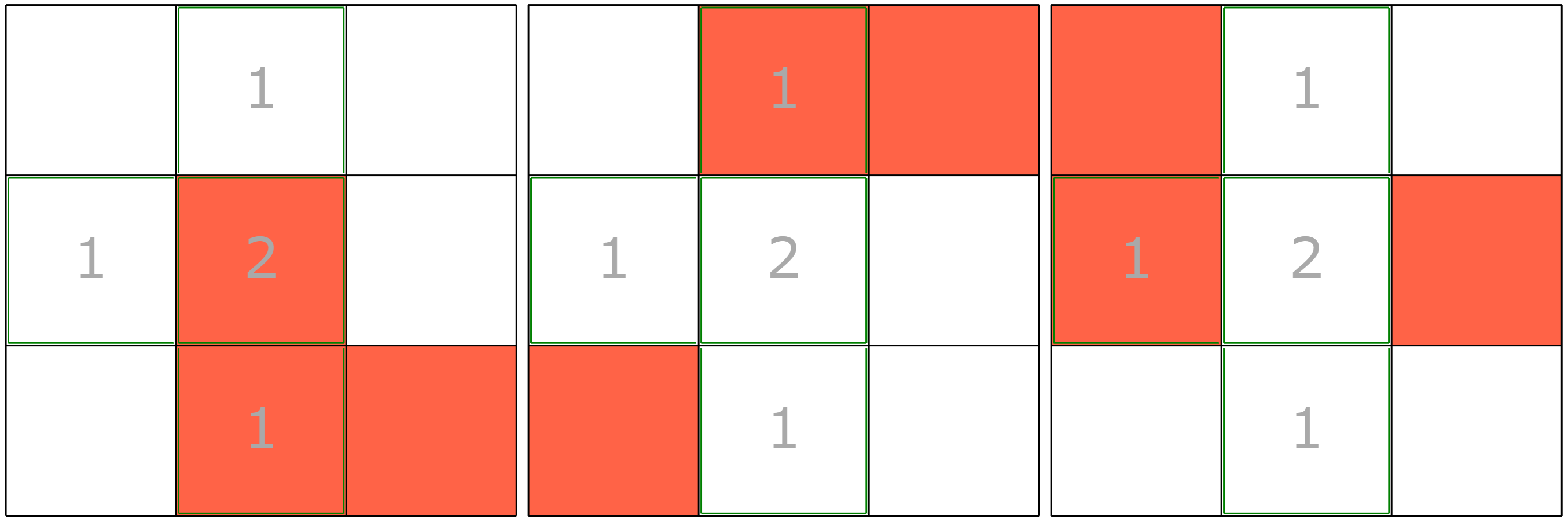
まず、適当に定めた範囲を占います。以下の例では島の大きさ$N=3$において、$T=3$回の占いを行う場合を示しました。赤いマスが占った範囲$S$を表しており、緑で囲われている石油が存在する箇所に注目すると、

1番目の占いでは範囲$S_1$を占って3単位の石油が見つかると期待される
2番目の占いでは範囲$S_2$を占って1単位の石油が見つかると期待される
3番目の占いでは範囲$S_3$を占って1単位の石油が見つかると期待される

という関係になっています。ただし、占い師の腕は十分に良く、誤差が無いと仮定しています。

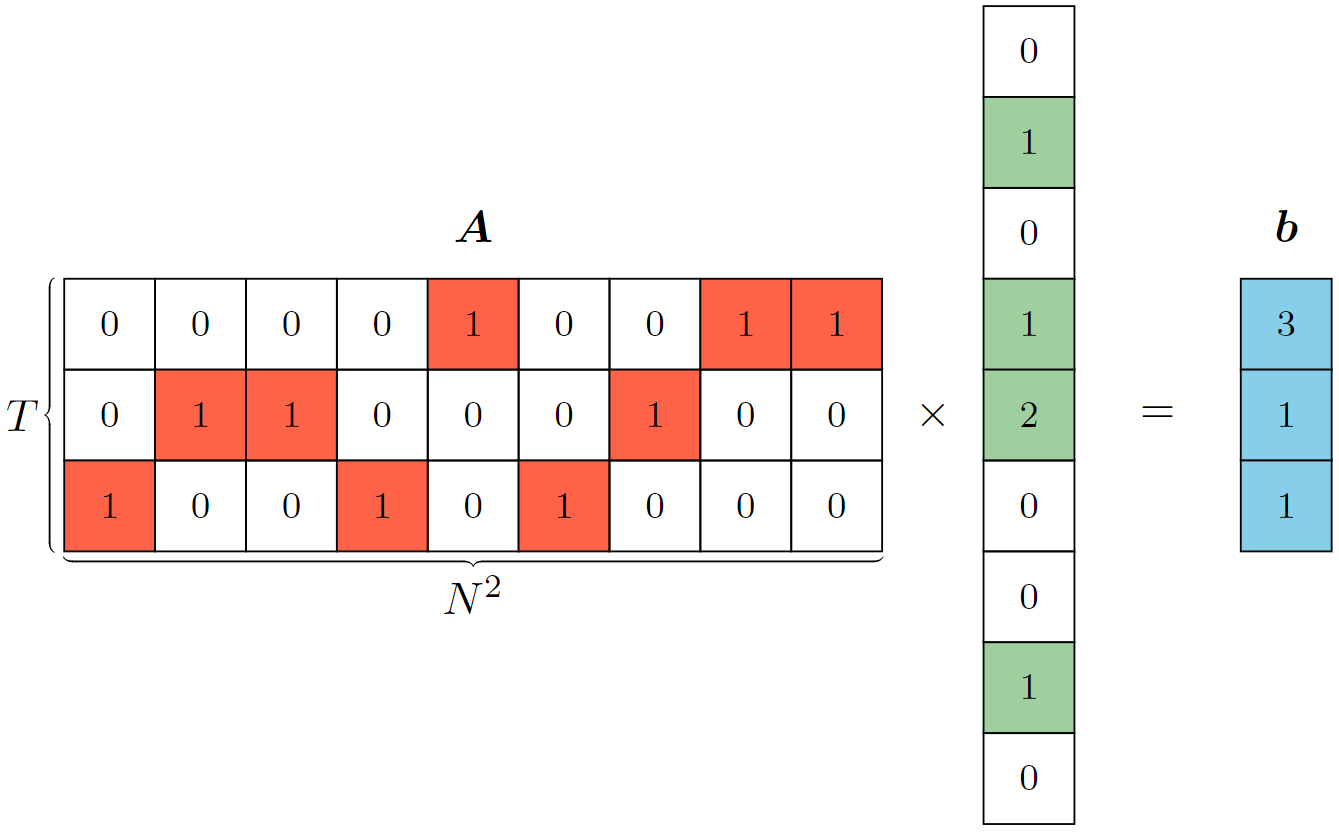
そして、このそれぞれの占い範囲$S$を$N^2$次元のベクトルを用いて表現し、それを縦に並べた行列$A$を考えます。

    A_{t,\mathrm{idx}} = \begin{cases}
        1 & \text{範囲$S_t$に$(i,j)$マスが含まれる場合 $(\mathrm{idx}=i \times N+j)$} \\
        0 & \text{それ以外の場合}
    \end{cases}

と定義しています。例えば$A$の1行目は1番目の占い範囲$S_1$に対応しています。そして、各マスにおける実際の石油埋蔵量を$N^2$次元のベクトル$\boldsymbol{x}$で表現すると、期待される占い結果は$(A\boldsymbol{x}=)\boldsymbol{b}$となり、その関係を上図では示しています。つまり、$\boldsymbol{b}$は$T$回の占い結果を並べたベクトルとなります。

さて、この関係を用いると本問題は

    A\boldsymbol{x}=\boldsymbol{b}

を満たす$\boldsymbol{x}$を求める問題に帰着されます。求めたいのは各マスの石油埋蔵量を表したベクトル$\boldsymbol{x}$だからです。占い結果に一切の誤差が無く、かつ行列$A$が列フルランクである場合、この方程式には一意に解が存在しますので、その解$\boldsymbol{x}$を求められます。

しかし、実際には占いに誤差が生じます。なので、完全な等号は成り立ちません。そこで代わりに、

    \lVert A\boldsymbol{x}-\boldsymbol{b} \rVert_1

を最小化したいと考えることも出来ます。ただし、$\lVert \cdot \rVert_1$は$L^1$ノルムを表しています。イメージとしては、$A\boldsymbol{x}$と$\boldsymbol{b}$の差分を可能な限り小さくしたいということです。この方針は線形計画問題を解くことに帰着されることが一般に知られており、実際にPuLPなどの線形計画ソルバーを用いて解かれている方もいらっしゃるようでした。

また、この定式化をさらに少し変えて、次の

    \lVert A\boldsymbol{x}-\boldsymbol{b} \rVert_2

を最小化したいと考えることも出来ます。ただし、$\lVert \cdot \rVert_2$は$L^2$ノルムを表しています。行列$A$が列フルランクである場合、その解析解が$(A^\top A)^{-1}A^\top \boldsymbol{b}$であることが一般に知られており、この方針で解かれている方もいらっしゃるようでした。

そして、これは二乗誤差最小化をしていると捉えることも出来ます。$\lVert A\boldsymbol{x}-\boldsymbol{b} \rVert_2^2$は、その定義より各占いの結果で出てくる誤差を二乗して足し合わせたものになっているからです。

さて、以上の話を基にして、本記事では何をお伝えしたいのかというと、この二乗誤差最小化の方針を精緻化すると、実はそれが最尤推定になっているということです。

最尤推定の導出

記事の後半にあたる本節では最尤推定の導出を行います。

この問題では、マス数$k_t$の範囲$S_t$において、その石油の埋蔵量$v(S_t)$とした時に、占い結果は平均$(k_t-v(S_t))\epsilon + v(S_t)(1-\epsilon)$分散$k_t\epsilon(1-\epsilon)$の正規分布に従うという設定でした（なお、これは二項分布を正規分布で近似したものになっています）。

そして、本来ではこの占い結果は非負整数に丸められるのですが、以下ではそれを無視して話を進めます。当然、本当はここを考慮した方が正しいですが数学的な議論の為に無視しています。詳しくは、競プロ文脈であればbowwowforeachさんによる誤差関数の話などを参照してください。

ここで、$t(1\leq t\leq T)$回目の占いについて、マス数$k_t$の範囲$S_t$における真の石油の埋蔵量を$v(S_t)$と置きます。また、その占い結果が$b_t$であるとします。

真の石油埋蔵量$v(S_t)$の最尤推定することは、次の最適化問題を解くことに等しいです。

  \max_{v(S_t)} \prod_{t=1}^{T} \frac{1}{\sqrt{2\pi k_t\epsilon(1-\epsilon)}} \exp\left(-\frac{\left((k_t-v(S_t))\epsilon + v(S_t)(1-\epsilon)-b_t\right)^2}{2k_t\epsilon(1-\epsilon)}\right)

この式は、平均$\mu$分散$\sigma^2$の正規分布の確率密度関数が

    f(b) =
    \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(b-\mu)^2}{2\sigma^2}\right)

であり、各占いが独立試行であることを踏まえると、目的関数は固定された石油の埋蔵状況に対してその占い結果が得られる確率を表しています。この確率を最大化することが最尤推定になります。

$k_t$は試行後においては既知の定数ですので、定数部分を取り払った上で自然対数を取ると、

  \max_{v(S_t)} \sum_{t=1}^{T} -\frac{\left((k_t-v(S_t))\epsilon + v(S_t)(1-\epsilon)-b_t\right)^2}{2k_t\epsilon(1-\epsilon)}

となります。

そして、正負を逆転させて最小化問題にすれば、

  \min_{v(S_t)} \sum_{t=1}^{T} \frac{\left((k_t-v(S_t))\epsilon + v(S_t)(1-\epsilon)-b_t\right)^2}{2k_t\epsilon(1-\epsilon)}

となります。この式が二乗の総和の形になっていることは注目に値します。つまり、これは二乗誤差最小化問題になっています。そこで、この最適化問題を$L^2$ノルムで表すと、

  \begin{align*}
  &\min_{v(S_t)} \sum_{t=1}^{T} \frac{\left((k_t-v(S_t))\epsilon + v(S_t)(1-\epsilon)-b_t\right)^2}{2k_t\epsilon(1-\epsilon)}\\

  =&
  \min_{\boldsymbol{v(S)}} \frac{1}{2\epsilon(1-\epsilon)}\sum_{t=1}^{T} \left(\frac{(1-2\epsilon)v(S_t)-(b_t-\epsilon k_t)}{\sqrt{k_t}}\right)^2\\

  =&
  \min_{\boldsymbol{v(S)}} \frac{1}{2\epsilon(1-\epsilon)}\left\lVert \frac{(1-2\epsilon)\boldsymbol{v(S)}-(\boldsymbol{b}-\epsilon\boldsymbol{k})}{\sqrt{\boldsymbol{k}}} \right\rVert_2^2\\

  =&
  \min_{\boldsymbol{v(S)}} \frac{1}{2\epsilon(1-\epsilon)}\left\lVert \frac{1-2\epsilon}{\sqrt{\boldsymbol{k}}}\boldsymbol{v(S)}-\left(\frac{\boldsymbol{b}-\epsilon\boldsymbol{k}}{\sqrt{\boldsymbol{k}}}\right) \right\rVert_2^2
  \end{align*}

となります。後半2行は厳密な書き方をしていませんが、例えば$\frac{1-2\epsilon}{\sqrt{\boldsymbol{k}}}\boldsymbol{v(S)}$は$\frac{1-2\epsilon}{\sqrt{k_t}}v(S_t)$を並べたベクトルであることなどを示しています。

最後に、この最適化問題を前半で定義した

試行ごとの範囲$S_t$をマスごとに表した行列$A$
マスごとの石油埋蔵量を表したベクトル$\boldsymbol{x}$
試行ごとの占い結果を表したベクトル$\boldsymbol{b}$

を用いて表現します。すると、$\boldsymbol{v(S)}$とは$A\boldsymbol{x}$に他ならないので、

  \min_{\boldsymbol{x}}
  \frac{1}{2\epsilon(1-\epsilon)} \left\lVert \frac{1-2\epsilon}{\sqrt{\boldsymbol{k}}}\boldsymbol{A}\boldsymbol{x} - \frac{\boldsymbol{b}-\epsilon\boldsymbol{k}}{\sqrt{\boldsymbol{k}}} \right\rVert_2^2

となり、係数などを無視して見ればこれは

    \min_{\boldsymbol{x}}
    \lVert A'\boldsymbol{x}-\boldsymbol{b}' \rVert_2^2

という$L^2$ノルム最小化問題そのものとなっています。これが最尤推定と二乗誤差最小化および$L^2$ノルム最小化の関係です。

実装について

おまけとして、上で述べた$L^2$ノルム最小化問題を実際に解く方法について述べます。これは一般にMoore–Penrose形一般化逆行列を用いて解けると知られています。そしてこの一般化逆行列は、特異値分解を用いて求められます。

従来のAtCoderにおけるC++では、これを求めるのにも一苦労だったと思いますが、直近の言語アップデートのお陰で行列ライブラリEigenが使えるようになりました。このEigenを使うことで、容易に求められます。私はEigenを今回初めて触ったのですが、かなり扱いやすく数時間程度で実装出来たので便利だと思います。ただ、他のEigenを使った方では、どうやらコンパイル時間が長くなりすぎてシステムテストの時にCEが出てしまったようでした。そこは少し注意が必要かも知れません。

以下にSeed=0,1,2に対する結果を示します。$2N^2-1$回ランダムな$N$マスに対して占いを行い、最後に$L^2$ノルム最小化問題を解きました。また、タブーサーチによる少しの工夫を施してはいます。

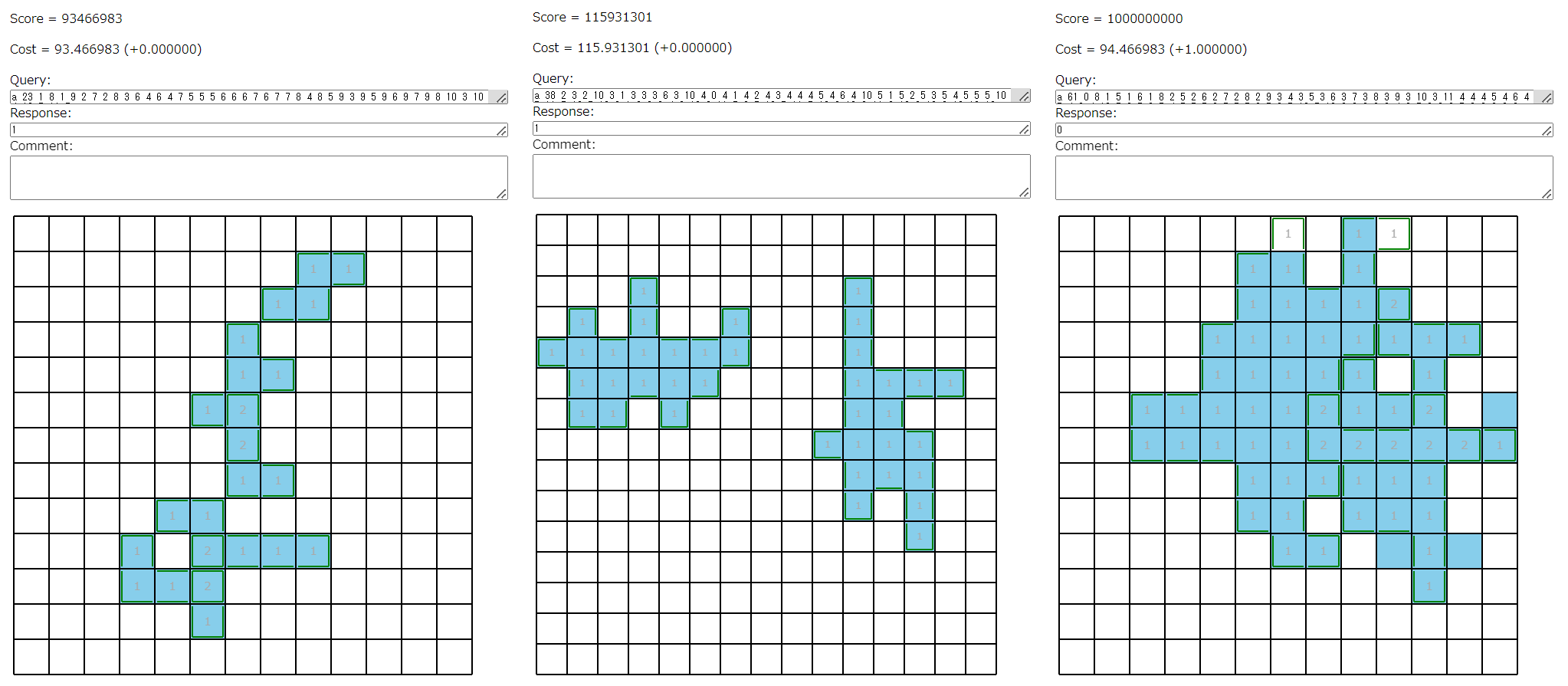
結果として

Seed=0: ほぼ確実に解が求まる
Seed=1: 乱数のシード次第では解が求まる
Seed=2: 解は求まらないが、それなりに近い解が求まる

という感じでした。

重要になるコードは以下の通りです。

void solveLS(const set<int>& taboo) {
    // Minimize ||Ax - b||_2^2
    // A:T \times SZ x:SZ b:T
    vector<int> activeIndexes;
    vector<int> rev(N * N, -1);
    for (int idx = 0; idx < N * N; idx++)
        if (taboo.count(idx) == 0) {
            rev[idx] = activeIndexes.size();
            activeIndexes.push_back(idx);
        }
    int T = sizes.size();
    const int SZ = activeIndexes.size();
    Eigen::MatrixXd A = Eigen::MatrixXd::Zero(T, SZ);
    Eigen::VectorXd b = Eigen::VectorXd::Zero(T);
    for (int tIdx = 0; tIdx < T; tIdx++) {
        double coeff = (1 - 2 * eps) / std::sqrt(eps * (1 - eps) * sizes[tIdx]);
        for (auto idx : placesPerTrial[tIdx])
            if (rev[idx] != -1) A(tIdx, rev[idx]) = coeff;
        b(tIdx) = (responses[tIdx] - eps * sizes[tIdx]) /
                  std::sqrt(eps * (1 - eps) * sizes[tIdx]);
    }
    Eigen::VectorXd x = A.colPivHouseholderQr().solve(b);
    answer.assign(N * N, 0);
    for (int idx = 0; idx < N * N; idx++)
        if (rev[idx] != -1) answer[idx] = max(0, int(round(x(rev[idx]))));
}

全容はこちらの提出にあります。154行です。

なお、冒頭でもお伝えした通り、この方針単体ではめちゃくちゃ悪い結果しか出せません。そもそも$N^2$回以上占いを行わないと劣決定系になってしまう、つまり解が一つに定まらない上に、連続緩和してしまっている、つまり占い結果や石油埋蔵量が整数値ではなく実数値として扱ってしまっているということが大きく響くからです。

なので、この方針はあくまで数学的な鑑賞用に近く、厳密にどこに石油があるかを求めたい本問とかなり相性が悪いです。そしてそれが没にした理由でもあります。

また、コンテスト中に実際に私が試したのは、EigenのunsupportedにあるNon-Negative Least Squares (NNLS)を使う方法です。こちらは非負制約が付きます。

現在のAtCoderでは、EigenのバージョンがEigen@3.4.0-2ubuntu2（出典:AtCoder）と少し古いのでこれを直接includeして使うことは出来ませんが、Mozilla Public License v. 2.0の下にGitHubで公開されており、コードを参照させて頂きました。

尤も、それでもやはりあまり上手くは行きませんでした。ポリオミノとして油田の形状が分かっているという情報を一切使っていない為、手法をちょっと改善した程度では本質的には変わらないと考えられます。試した当時は非負制約まで入れるとどこまで解が良くなるかは未知数だなと思っていたのですが、今振り返るとやはりその情報が使えていない時点であまり筋が良いとは言えません。

この辺の上手く行く/行かないの直感が自分にはまだまだ足りていないと痛感しました。

最後に

本記事は、AHC030の没解法について述べました。

まとめると、

二乗誤差最小化と最尤推定は本質的に同値である
言語アップデートにより使えるようになったEigenを用いることで簡単にこれは解ける
ただし、離散/連続のギャップなどの為に実際にはあまり使えない

ということでした。

実は私が最初に思いついていたのはLPを用いた$\lVert A\boldsymbol{x}-\boldsymbol{b} \rVert_1$の最小化でした。私のバックグラウンドの都合上、全ての問題がLPに見える病気にかかってしまっているので最悪です。

ただ、その後よくよく考えるとこれは二乗誤差最小化にした方が最尤推定の観点からは正しく、それに計算量の観点からも優れているのだなと気付きました。そのことは私の知らない話で面白く感じたので本記事に書いてみました。既にご存知の方からすれば何を当たり前なことをと思われているかも知れませんが……。

また、コンテスト終了後にTwitter(現X)にて様々な解法を目にしましたが、この話を基にするとそれらが統一的に解釈できる節があります。皆がてんでばらばらに解いた結果、実は根底に通ずるものがあるというのも、かなり面白いと感じました。この記事の読者の中にも、いずれかの方針に近いやり方で解いた方がいらっしゃれば嬉しく思います。

以上です。読んで頂きありがとうございました。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up