「凸関数は連続である」という言説の落とし穴

開区間上で定義された凸関数は連続です。この意味で、「凸関数は連続である」と言えます。

しかし、閉区間上で定義された凸関数は区間の端点で連続であるとは限りません。

では、そういう自明な例外しかないんですね、と分かった気でいると、こういう例が落とし穴になります。下図で青点 $(0,0)$ は連続点なように見えますが、赤で示した $(0,0)$ に収束する点列を考えると、実は不連続点です。

本記事の内容は、Nesterovによる"Lectures on Convex Optimization"¹に一部準拠します。以下、教科書と表記します。

概要

本記事では以下のフローチャートに基づき説明します。

定義

厳密な議論の為に定義を示します。

凸関数

集合 $Q$ が 凸(convex) であることは、次と同値です。（教科書 Definition 2.1.1）

\alpha x + (1 - \alpha) y \in Q \quad (\forall x, y \in Q, ~ \forall \alpha \in [0, 1])

凸集合である	凸集合でない

(Wikipedia「凸集合」より引用 / CheCheDaWaff, CC BY-SA 4.0, via Wikimedia Commons)

また、拡大実数に値を取る関数 $f\colon \mathbb{R} \to \mathbb{R} \cup \lbrace \pm\infty \rbrace$ の domain は次のように定義されます。

\mathrm{dom} ~ f = \lbrace x \in \mathbb{R}^n \mathrel{\mid} \lvert f(x) \rvert < \infty \rbrace

つまり、実数の範囲内に値を取る点の集合です (effective domainとして $-\infty$ の場合を含めることもあります)。本記事および教科書では $\mathrm{dom} ~ f \neq \emptyset$ を仮定します。

なお、真凸関数 (proper convex function)²は $\mathrm{dom} ~ f \neq \emptyset$ と $f(x) \neq -\infty$ が条件の為、代わりに真凸関数であることを仮定しても殆ど同じ議論になります。

そして、$f$ が 凸関数 であることは、$\mathrm{dom} ~ f$ が凸であり、かつ、次を満たすことと同値です。（教科書 Definition 3.1.1）

\begin{gather*}
f(\alpha x + (1 - \alpha) y) \leq \alpha f(x) + (1 - \alpha) f(y) \\
(\forall x, y \in \mathrm{dom} ~ f,~\forall \alpha \in [0, 1])
\end{gather*}

連続

関数 $f$ が $\mathrm{dom} ~ f$ で連続であることは、任意の $\overline{x} \in \mathrm{dom} ~ f$ において $f$ が連続であることと同値です。

ある $\overline{x} \in \mathrm{dom} ~ f$ において $f$ が連続であることは、$\overline{x}$ に収束する任意の点列 $\lbrace x_k \rbrace \subseteq \mathrm{dom} ~ f$ に対し、$\lbrace f(x_k) \rbrace$ が $f(\overline{x})$ に収束すること、すなわち、

\lim_{k \to \infty} x_k = \overline{x} \implies \lim_{k \to \infty} f(x_k) = f(\overline{x})

が成立することと同値です³。

Section 1: dom f が実数全域となる凸関数は連続である

本節では以下の命題を示します⁴。

凸関数 $f\colon \mathbb{R}^n \to \mathbb{R}$ は連続である。

言い換えると、次と等価です。

$\mathrm{dom} ~ f$ が実数全域となる （i.e. $\pm \infty$ に値を取らない) 凸関数は連続である。

直感的には、各点の回りで適切な近傍が取れるので、変な不連続性が生じない、ということです。

$ax+b, x^2, | x |, e^x$ などの関数が該当します。ただし、$1/x$ や $-\log x$ すら、この「$\mathrm{dom} ~ f$ が実数全域となる」という条件を満たさないことに注意して下さい。

「dom fが実数全域となる凸関数は連続である」の証明

話の本筋ではない為、以下に折りたたんで証明を示しました。必要な方はお読みください。

証明 （ここを押して読んで下さい）

任意の $\overline{x} \in \mathbb{R}^n$ に対して、$f$ が $\overline{x}$ で連続だと示します。

ある $M$ が存在して、$\lVert x - \overline{x} \rVert \leq 1$ を満たす任意の $x \in \mathbb{R}^n$ に対し、$\lvert f(x) - f(\overline{x}) \rvert \leq M$ と出来ます。 $f(x) \in \mathbb{R}$ が $\pm \infty$ でなく、有限値を取る為です。

任意の $0 < r \leq 1$ に対し、$\lVert x-\overline{x} \rVert = r$ を満たす $x \in \mathrm{dom} ~ f = \mathbb{R}^n$ が存在します。 $\overline{y}_1, \overline{y}_2 \in \mathrm{dom} ~ f$ を

\overline{y}_1 := \overline{x} + \frac{x-\overline{x}}{r}, \quad \overline{y}_2 := \overline{x} - \frac{x-\overline{x}}{r}

と定義します。$\lVert \overline{y}_1 - \overline{x} \rVert = \lVert \overline{y}_2 - \overline{x} \rVert = 1$ より、$\lvert f(\overline{y}_1) - f(\overline{x}) \rvert \leq M,$ $\lvert f(\overline{y}_2) - f(\overline{x}) \rvert \leq M$ が成立します。

ここで、

\begin{align*}
        & - f\left(\overline{{x}} - \frac{x - \overline{x}}{r} \right) +  f(\overline{x})\\
\leq {} & \left(\frac{1}{r} f(x) - \frac{1+r}{r}f(\overline{x})\right)+ f(\overline{x})\\
= {} & \frac{f(x) - f(\overline{x})}{r}\\
= {} & \left(\frac{1}{r}f(x) - \frac{1-r}{r}f(\overline{x})\right) - f(\overline{x})\\
\leq {} & + f\left(\overline{x} + \frac{x - \overline{x}}{r}\right) - f(\overline{x})
\end{align*}

が成立します。不等式はそれぞれ適切に変形すると $f$ が凸である定義式より導かれます。$\overline{y}_1,$ $\overline{y}_2,$ $M$ の定義より、

\begin{align*}
    & \left\lvert \frac{f(x) - f(\overline{x})}{r} \right\rvert \\
\leq {}& \max \left( \lvert f(\overline{y}_1) - f(\overline{x}) \rvert, \lvert f(\overline{y}_2) - f(\overline{x}) \rvert \right) \\
\leq {}& M
\end{align*}

が導けます。直感的には $M$ が半径1の範囲内における最大の傾きの絶対値を意味し、凸性から上記の値は $M$ 以下になるということです。

$r$ は任意だったので、$r \to 0$ とすれば、$f(x) \to f(\overline{x})$ が得られ、$f$ は $\overline{x}$ で連続だと示されます。

よって、$f$ は連続であり、$\mathrm{dom} ~ f$ が実数全域となる凸関数は連続です。

Section 2: 閉凸関数でない場合、連続性は様々あり得る

続いて、$\mathrm{dom} ~ f \neq \mathbb{R}^n$ である場合について考えます。つまり、$\pm \infty$ に値を取ることがある場合です。

閉凸の定義

まず、エピグラフを定義します。関数 $f\colon \mathbb{R}^n \to \mathbb{R}$ の エピグラフ(epigraph) は次のように定義されます。

\mathrm{epi} ~ f = \lbrace (x, t) \in \mathbb{R}^{n+1} \mathrel{\mid} x \in \mathrm{dom} ~ f, ~ f(x) \leq t \rbrace

連続性を議論する上で重要な性質が閉凸です。関数 $f$ が 閉凸 であることは、エピグラフが閉集合であることと同値です。（教科書 Definition 3.1.2）

閉凸	閉凸

右の例では、$\mathrm{dom} ~ f$ は $\lbrace x \in \mathbb{R} \mathrel{\mid} x > 0 \rbrace$ と開区間ですが、閉凸関数です。

また、以下は閉凸でない例です。

閉凸でない	閉凸でない

定義と見比べて下さい。

連続でない例

凸関数に閉凸という条件を課さない場合、連続な例（開区間上の凸関数）や、不連続な例が容易に構築出来ます。先にも示した、以下は不連続な凸関数です。

この関数が凸関数であることは、凸関数の定義

\begin{gather*}
f(\alpha x + (1 - \alpha) y) \leq \alpha f(x) + (1 - \alpha) f(y) \\
(\forall x, y \in \mathrm{dom} ~ f,~\forall \alpha \in [0, 1])
\end{gather*}

において、$x$ または $y$ が区間の左端である時のみ非自明ですが、確かに定義を満たしています。よって、閉凸でないなら、容易に不連続な例は作れます。

余談として、以下の例は不連続ですが、そもそも非凸です。不連続点が $\mathrm{dom} ~ f$ の境界になければならないのは、凸性の担保の為と言えます。

以上で、閉凸関数ではないという、ある種自明な例外を議論しました。

ここで、閉凸関数であるという条件を課した時、不連続な例が存在するのか否かは、かなり非自明な問いです。それが実は存在する、ということを次節で示します。

Section 3: 閉凸関数でも不連続になり得る

本節では、$\mathrm{dom} ~ f \neq \mathbb{R}^n$ かつ閉凸関数である場合について考えます。この場合、次の事実が成り立ちます。

• 2変数以上の場合、$f$ は連続であるとは限らない。
• 1変数の場合、$f$ は連続である。

これらをそれぞれ証明します。

Section 3.1: 2変数以上の場合

2変数以上の場合、閉凸関数であっても連続であるとは限らないことを、反例で示します。

$g\in \mathbb{R}^n$ と $\gamma \in \mathbb{R}$ に対して、

\begin{align*}
\phi(y,g,\gamma) &:= \langle g, y \rangle - \frac{\gamma}{2} \| y \|_2^2 \\\\
\psi(g,\gamma) &:= \sup_{y \in \mathbb{R}^n} \phi(y,g,\gamma)
\end{align*}

と定義します。$\langle \cdot, \cdot \rangle$ は内積、$\lVert \cdot \rVert_2$ はユークリッドノルムです。これが凸関数であることの証明は比較的容易なので省略します。詳細は教科書を参照して下さい。

$\psi(g,\gamma)$ の具体的な値は以下のようになります。

\psi(g,\gamma) = \begin{cases}
0 & g=0,~\gamma=0\\
\frac{\| g \|_2^2}{2\gamma} & \gamma > 0\\
\infty & \text{otherwise}
\end{cases}

具体的な値の計算（ここを押して読んで下さい）

$\psi(g,\gamma)$ の挙動を $\gamma$ で場合分けして調べます。

• $g=0,~\gamma=0$ の場合

$\phi(y,0,0) = 0$ より $\psi(0,0) = 0$ です。

• $\gamma>0$ の場合

\begin{align*}
\psi(g,\gamma) &= \sup_{y \in \mathbb{R}^n} \left( \langle g, y \rangle - \frac{\gamma}{2} \| y \|_2^2 \right) \\
&= \sup_{y \in \mathbb{R}^n} \left( -\frac{\gamma}{2} \left\| y - \frac{g}{\gamma} \right\|_2^2 + \frac{\| g \|_2^2}{2\gamma} \right) \\
&= \frac{\| g \|_2^2}{2\gamma}
\end{align*}

です。

• $g \neq 0,~\gamma=0$ または $\gamma<0$ の場合

$g\neq 0,~\gamma \leq 0$ の場合、$y_\alpha = \alpha g$ とすると、

\begin{align*}
\phi(y_\alpha,g,\gamma) &= \langle g, \alpha g \rangle - \frac{\gamma}{2} \| \alpha g \|_2^2 \\
&= \alpha \| g \|_2^2 - \frac{\gamma}{2} \alpha^2 \| g \|_2^2 \\
&\to \infty \quad (\alpha \to \infty)
\end{align*}

より、$\psi(g,\gamma)=\infty$ です。

$g=0,~\gamma < 0$ の場合、$\phi(y,0,\gamma) = -\frac{\gamma}{2} | y |_2^2$ より、$\psi(0,\gamma)=\infty$ です。

以上より、$\psi(g,\gamma)=\infty$ です。

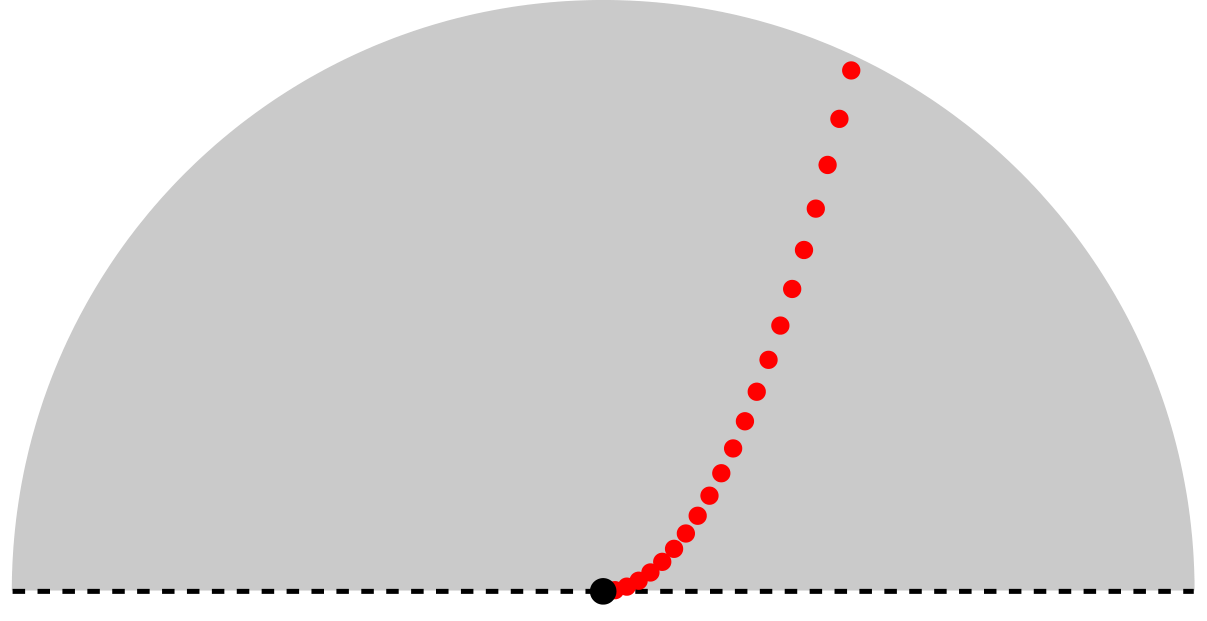
これを $n=1$ の場合に図示すると、冒頭にも示した以下のグラフになります。

図では $\gamma$ の下限を少しずつ変えて示しています。このグラフは青点 $(g,\gamma)=(0,0)$ において $\phi(g,\gamma)=0$ ですが、$g \neq 0$ では $\gamma \to 0$ において $\phi(g,\gamma) \to \infty$ です。

ここで、赤の点列は、ある $\beta>0$ に対し、

\begin{cases}
\displaystyle \lim_{k \to \infty} (g_k,\gamma_k)= (0,0) \\
\displaystyle \lim_{k \to \infty} \psi(g_k,\gamma_k)= \beta
\end{cases}

を満たす点列です。$\gamma > 0$ において $\psi(\sqrt{\gamma}g,\gamma) = \frac{1}{2} \lVert g \rVert_2^2$ であることを用いると作れます。これは明らかに $\psi$ が不連続だと示しています。

さらに面白い点として、$\mathrm{dom} ~ \psi =$ $(\mathbb{R} \times \lbrace \gamma > 0 \rbrace) \cup \lbrace (0,0) \rbrace$ は閉でも開でもないですが、$\psi$ は閉凸関数です。

$n=1$ で $\psi$ が閉であることを証明します。

一般に、ある関数 $f$ が閉である、つまりエピグラフ $\lbrace (x,t) \mathrel{\mid} x \in \mathrm{dom} ~ f,~ f(x) \leq t \rbrace$ が閉集合であることは、任意の $c \in \mathbb{R}$ に対して、劣位集合(sublevel set) $\lbrace x \in \mathrm{dom} ~ f \mathrel{\mid} f(x) \leq c \rbrace$ が閉集合であることと同値です。十分性は自明で、必要性も点列を用いた議論などで示せます。

ここで、ベクトル $g$ の唯一の成分のことも $g$ と表記すると、

\psi(g,\gamma) \leq c \iff \frac{1}{2c} g^2 \leq \gamma

であって、これは放物線の上側部分で閉集合です。
よって、任意の劣位集合が閉集合であり、$\psi$ は閉、特に閉凸関数であることが示されました。

この小節のまとめとして、以下のことを強調しておきます。

2変数以上の閉凸関数 $f$ は $\mathrm{dom} ~ f$ で連続であるとは限らない。

Section 3.2: 1変数の場合

1変数の場合、閉凸関数 $f$ は $\mathrm{dom} ~ f$ で連続であることを示します。上記2変数の場合との違いに注目して下さい。

つまり、以下などが連続です。

系として開区間で定義された凸関数の連続性が従います。なお、この事実はかなり簡単に示せますが、そのような証明は別の記事⁵などを参照して下さい。

では、1変数の閉凸関数 $f$ が $\mathrm{dom} ~ f$ で連続であることを示します。

「1変数の閉凸関数はdom fで連続である」の証明

任意の $\overline{x} \in \mathrm{dom} ~ f \subseteq \mathbb{R}$ に対して、$f$ が $\overline{x}$ で連続だと示します。

点列 $\lbrace x_k \rbrace \subseteq \mathrm{dom} ~ f$ が $\overline{x}$ に収束するとします。

Appendixに示すように、$f$ は閉凸ならば下半連続です。つまり、以下は一般に成立します。

\liminf_{k \to \infty} f(x_k) \geq f(\overline{x})

この時、

\limsup_{k \to \infty} f(x_k) \leq f(\overline{x})

であることを示せば、上極限と下極限が一致する⁶為、その極限は $f(\overline{x})$ に一致し、$f$ が $\overline{x}$ で連続であることが示されます。

非常に重要な事として、1変数、つまり、数直線上の凸関数のdomainは、それが凸集合であるという性質上、一つの区間の形以外にありえません。また、$\mathrm{dom} ~ f \neq \emptyset$ であることを仮定しています。

つまり、$x_k \to \overline{x}$ より、$k$ が十分大きい任意の $x_k$ は、高々2つの固定された $\overline{y}_1, \overline{y}_2\in \mathrm{dom} ~ f$ を用いて、

x_k \in \lbrace (1-\alpha_k) \overline{x} + \alpha_k \overline{y}_1, (1-\alpha_k) \overline{x} + \alpha_k \overline{y}_2 \rbrace \quad (\alpha_k \in [0, 1])

と表せます。

例えば以下の図では、赤点が $\lbrace x_k \rbrace$ を示しますが、十分 $\overline{x}$ に近い点は、そのように表せることが分かります。

また、凸関数の定義より、

\begin{cases}
f(x_k) \leq (1-\alpha_k) f(\overline{x}) + \alpha_k f(\overline{y}_1) \\
f(x_k) \leq (1-\alpha_k) f(\overline{x}) + \alpha_k f(\overline{y}_2)
\end{cases}

のいずれかが成立します。

ここで、$x_k \to \overline{x}$ より、$\alpha_k \to 0$ が導かれます。そして、上記不等式で $\alpha_k \to 0$ とすると、

\limsup_{k \to \infty} f(x_k) \leq f(\overline{x})

が導かれます。これは、$f$ が $\overline{x}$ で上半連続であることを示しています。

よって、$f$ は $\overline{x}$ で連続であり、特に、$f$ は $\mathrm{dom} ~ f$ で連続です。

2変数関数の場合、何故証明が回らないのか

補足として、上の証明が何故2変数以上の場合に回らないのか、という点について考察します。

関数 $\psi$ は、閉凸関数だが連続ではない2変数関数でした。

そのdomainである $\mathrm{dom} ~ \psi =$ $(\mathbb{R} \times \lbrace \gamma > 0 \rbrace) \cup \lbrace (0,0) \rbrace$ および赤の点列を2次元平面上にプロットしたのが下図です。

この点列では、先の証明で仮定した $\overline{y}_1,~\overline{y}_2$ に相当するものが無限個必要になってしまいます。これでは $x_k \to \overline{x}$ としても、$\alpha_k \to 0$ とは限らないため、先の証明が回らないのです。

ここに1変数の場合と2変数以上の場合の決定的な違いがあると考えています。

まとめ

本記事では、凸関数の連続性について、以下のことを示しました。

理解の一助になれば幸いです。

Appendix 閉凸関数ならば下半連続である

補足として、閉凸関数ならば下半連続であるという主張を示します(教科書 Theorem 3.1.4.1)。先述の通り、閉凸関数は連続であるとは限らないですが、それを弱めた性質が下半連続性であり、それは成立するということです。

本節では、下半連続の定義を示し、その後に閉凸関数ならば下半連続であることを示します。

下半連続の定義

ある $\overline{x} \in \mathrm{dom} ~ f$ において $f$ が下半連続であることは、$\overline{x}$ に収束する任意の点列 $\lbrace x_k \rbrace \subseteq \mathrm{dom} ~ f$ に対し、

\liminf_{k \to \infty} f(x_k) \geq f(\overline{x})

が成立することと同値です。下図も参照して下さい。

(Wikipedia「半連続」より引用 / Mktyscn, Public domain, via Wikimedia Commons)

実際、$\psi$ の例でも $(\overline{g},\overline{\gamma})=(0,0)$ に収束する赤点で示した点列も、関数値 $\psi$ は $\beta>0$ に収束し、

\liminf_{k \to \infty} \psi(g_k,\gamma_k) = \beta \geq \psi(0,0) = 0

を満たしています。

（なお、本記事では省略しますが真凸関数かつ閉凸関数であることの必要十分条件は、それが下半連続である⁷ことです）

「閉凸関数ならば下半連続である」の証明

$f$ が閉凸関数ならば下半連続であることを示します。

$\overline{x}$ に収束する任意の点列 $\lbrace x_k \rbrace \subseteq \mathrm{dom} ~ f$ に対し、点列 $\lbrace (x_k, f(x_k)) \rbrace \subseteq \mathrm{epi} ~ f$ を考えます。

\liminf_{k \to \infty} f(x_k) =: \overline{f} \geq f(\overline{x})

が言えれば良いです。

$\overline{f}$ の値に基づく場合分けを行います。なお、$\overline{f}$ は常に拡大実数 $\mathbb{R} \cup \lbrace \pm\infty \rbrace$ 内に存在します。$\liminf$ になじみがない方は、文献⁶も参考にして下さい。

• $\overline{f} \in \mathbb{R}$ の場合

$\liminf$ の性質⁶より、ある部分列 $\lbrace f(x_{k_j}) \rbrace$ が $\overline{f} \in \mathbb{R}$ に収束します。$\lbrace x_k \rbrace$ は $\overline{x}$ に収束する点列でした。なので、収束部分列の性質⁸として、$x_{k_j}$ も $\overline{x}$ に収束します。以上より、$\lbrace (x_{k_j}, f(x_{k_j})) \rbrace$ は $(\overline{x}, \overline{f})$ に収束します。

ここで、閉凸関数の定義より $\mathrm{epi} ~ f$ は閉集合である為、その内で定義される任意の点列は、極限を持つならばそれは $\mathrm{epi} ~ f$ 内に存在します。

よって、点列 $\lbrace (x_{k_j}, f(x_{k_j})) \rbrace$ は $(\overline{x}, \overline{f})$ という極限を持つため、それは $\mathrm{epi} ~ f$ 内に存在します。つまり、

(\overline{x}, \overline{f}) \in \mathrm{epi} ~ f
\iff
\overline{f} \geq f(\overline{x})

が成り立ち、主張は成立します。

• $\overline{f} = -\infty$ の場合

条件より $\liminf_{k \to \infty} f(x_k) = -\infty$ です。$\overline{x} \in \mathrm{dom} ~ f$ なので $f(\overline{x})-1$ は固定された実数値です。よって、ある部分点列 $\lbrace x_{k_j} \rbrace$ が存在し、$f(x_{k_j}) \leq f(\overline{x})-1$ が成り立ちます。$\mathrm{epi} ~ f$ の定義より $\lbrace (x_{k_j}, f(\overline{x})-1) \rbrace \subseteq \mathrm{epi} ~ f$ で、収束先は $(\overline{x}, f(\overline{x})-1)$ です。

先程と同様に閉性よりこれは $(\overline{x}, f(\overline{x})-1) \in \mathrm{epi} ~ f$ を導きます。

しかし、これは $f(\overline{x}) \leq f(\overline{x})-1 \iff 0 \leq -1$ を意味し矛盾です。なので、そもそもの仮定が誤りだと分かります。

• $\overline{f} = \infty$ の場合

この場合、$\overline{f} = \infty \geq f(\overline{x})$ は自明です。

以上より、場合分けは尽くされ、

\overline{f} = \liminf_{k \to \infty} f(x_k) \geq f(\overline{x})

が成り立ち、$f$ は $\overline{x}$ で下半連続です。

謝辞

本記事は所属研究室の輪読準備の一環として書かれました。
研究室の皆様に感謝致します。

1. Nesterov, Yurii. Lectures on convex optimization. Vol. 137. Berlin: Springer, 2018. ↩

2. Wikipedia. 真凸関数. 2022. ↩

3. MATHPEDIA. 位相空間論5:連続写像 (命題 5.18). 2021. ↩

4. Misha Lavrov. Is a convex function always continuous?. Stack Exchange, 2018. ↩

5. 数学の景色. 凸関数と凸不等式(イェンセンの不等式)についてかなり詳しく. 2023. ↩

6. 数学の景色. 上極限,下極限(limsup,liminf)の定義と例と性質2つ. 2022. ↩ ↩² ↩³

7. Wikipedia. 閉凸函数. 2016. ↩

8. 野村数学研究所. 点列の収束と任意の部分列の収束. ↩