概要
注意書き
本記事はAHC014という、AtCoderで開催された株式会社estieさんによるヒューリスティックコンテストの参加記、および、解説記事です。
先日開催されたAHC014というヒューリスティックコンテストに出場し、24位になりました。
本記事では、私の解法の概略と問題の性質について少し書かせて頂きます。
今回の問題において、上位勢はその殆どが焼き鈍しというメタヒューリスティックを用いていましたが、私はそれとは別のビームサーチという手法を用いました。
上記リンクにある解説放送における40:35あたりからの、writerであるwataさんの発言によれば、
「(ビームサーチなどの手法は)今回の問題はあまり向いていなさそう」
「少なくとも生のスコアを使ってビームサーチする限りうまく行かない」
などとのことでした。
結論から述べれば全く以って仰る通りなのですが、しかし、実はビームサーチという方針で、かつほぼ生のスコアを使ったとしても、24位くらいにはなれる(そして、恐らくその辺りがほぼ限界かも知れない)ということをお伝えしたく、本記事を執筆しています。
なお、自分より上位の方のコードをざっと見た限り、既に解説記事を書いていらっしゃるpenguin46さんを除いて、「beam」という単語はソースコードに出ていなかったので(かつpenguin46さんも焼き鈍し解のようなので)、恐らく私の解が提出者の中では一番良いビームサーチをメインとした解のようです。
くどい説明もあるかと思われますが、皆様にとって以下の解説が何らかの助けになれば幸いです。
問題
解法
具体的な解法を述べる前に、段階的に前提となる事項を整理していきます。
問題の性質に関する前提
前提A_1 一辺の長さが1の正方形をメインに考える
これは解説放送でも触れられていましたが、基本的には小さい矩形領域を使用した方がよいです。大きい長方形などを使ってしまうと、使用できる辺の本数が減ってしまい、結果として新たに置ける点の個数も減るので無駄が生じてしまいます。
この記事における「長さ」の定義を、感覚的には$max(abs(dx),abs(dy))$で定めるとしてやると、長さが1の正方形は当然以下の二つのみです。
(なお、私の方針では、基本的に点よりも線の方が重要なので、新たに追加された点が正方形の4頂点のいずれであるかなどは、今は考えないでもらって大丈夫です)
これらをメインに以下考えていきます。
前提A_2 長さ1の正方形はいくつかの種類に分類して考えることが出来る
先の前提A_1で考えた正方形について、(あくまで独自の用語ですが)縦横格子と斜め格子の二つに分類して考えることが出来る、つまり、傾いていない正方形と傾いている正方形でそれぞれ分類して考えることが可能で、どの辺を使用するかということはそれぞれ独立に決めて良い、ということは多くの方に直感的に理解して頂けることかと思います。
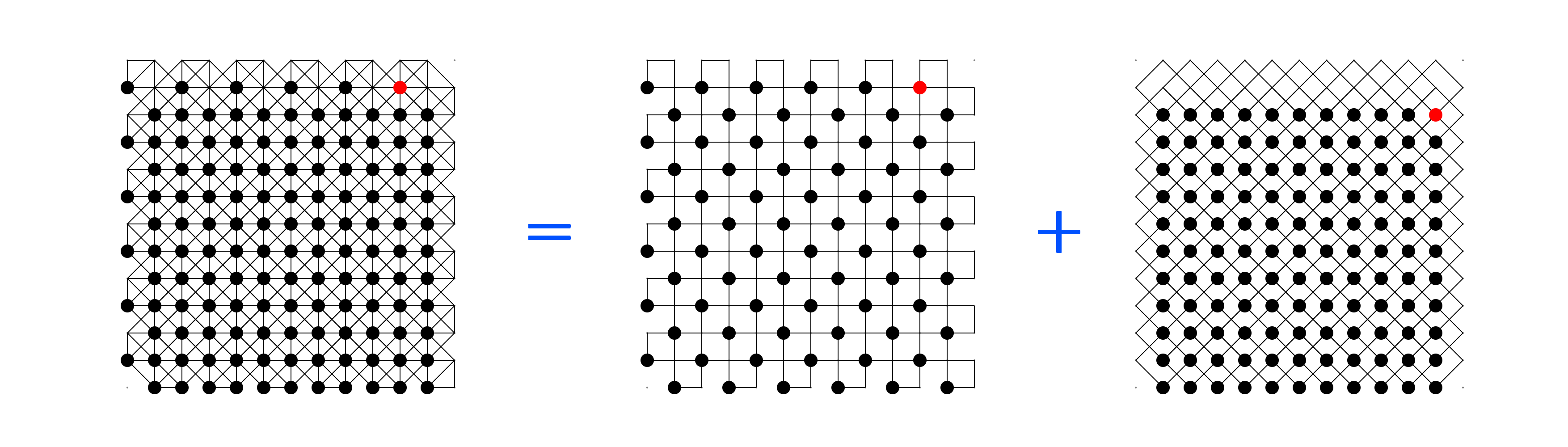
ところで、この縦横格子ですが、辺を重複しないような最も綺麗な(最密充填な)敷き詰め方は、偶奇性(以下パリティと書きます)に注目すると以下の2パターン存在します。分かりやすさの為、正方形内部に色を付けています。
この時、一方のパリティに属する正方形を採用すると、他方のパリティに属する正方形は最大4つ失われてしまうということがご覧いただけるでしょうか。
上下左右の辺を、それぞれ一つずつ他方のパリティに属する正方形が使用している場合に、あわせて4つの損失ということです。
これは明らかに望ましいとは言えません。出来るだけ長方形を多く描きたいという状況において、もしそれぞれのパリティが入り乱れて使用されてしまえば、それだけ多くの候補が失われてしまいます。
結局、このパリティをどちらか一方に制限すれば、もう一方のパリティの正方形は全て使えなくなるものの、確実に最大数の正方形を使用できることが出来るので、もしかしたらこの「パリティをどちらかに決め打つ」ということは有効な手段かも知れないと考えられます。
(無論、制限があればそれだけ自由は損なわれるので、この時点ではまだ必ずしも有効な手段とは言えないです。)
斜め格子についても考えてみます。
同様に、辺の集合を被らせないということを意識すると、x座標に関するパリティによって以下の2パターンに分類することが可能です。
これまた、一方のパリティに属する正方形を採用すると、他方のパリティに属する正方形は右上、右下、左下、左上の最大4つが失われてしまいます。
これに関してもどちらかのパリティに決め打てば、もしかしたらうまく行くかもしれません。
そして、x座標とy座標は概念として対等なので、これを90度回転し、y座標に関するパリティにのみ注目した議論も可能になってきます。
ともかく、一見するとどれも同じ長さ1の正方形ではありますが、実はこれらはいくつかのパリティによる分類を有している、という観点が重要になってきます。
前提A_3 雪崩の発生が多くの他の現象より有意に強い
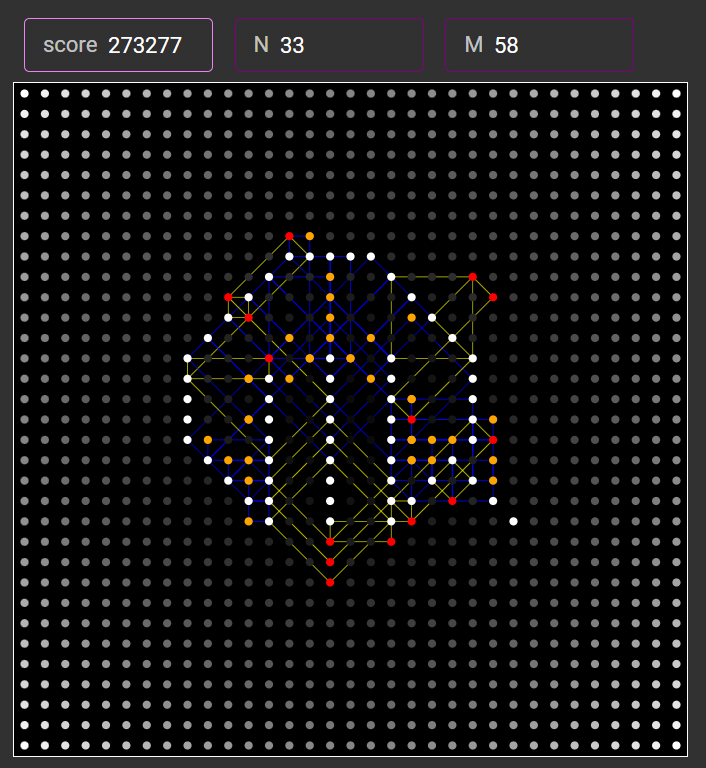
ここで、とあるビジュアライザ結果を見てみましょう。
かえでさんによる解説記事にも登場していたので、ご存じの方も多いかも知れませんが、しましまさんという方が、初日の時点で極めて高いスコアのビジュアライザ結果を共有されていました。
この画像の特に下部の部分では、どうやら連鎖的に外側へ長方形が伸びていく機構が確認できます。
本来の点配置が以下のestieさんのロゴなので、元々点は全くない箇所のはずです。
このような、無から有を創り出している現象が存在するのだというヒントを、ビジュアライザから得ることが出来ます。
そして、これまた独自の用語で恐縮ですが、その連鎖的に発生していく様に注目して、この現象を雪崩と私は勝手に名前を付けて考察していました。以下でもこの用語を使用します。
その後の共有されたビジュアライザ結果を見ても、良いスコアを獲得している者はほぼ必ず雪崩が起こっているので、どうやら雪崩を発生させることが、他の方針よりも強そうだということが分かります。
(余談ですが、私は最初の3日間はビジュアライザを自分で移植してずっと手動解を作り続けていました。その過程を経ても、やはりどうにも雪崩以上に強い現象は存在しないだろうということが確認できたので、それなりに自信をもって考察することが出来ました。ビジュアライザの作成はそういった実装前の考察にも役立つので、個人的にはお勧めです)
前提A_4 雪崩の発生条件を整理する
さて、ではその強いと目される雪崩の発生を目指していきます。
結論から述べますが、雪崩は以下のような手順によって発生していきます。
傾いている正方形と傾いていない正方形がおよそ交互に全ての辺(枠)を使い切るように使用していけば、雪崩は上手く発生します。
この時、先程述べた前提A_2とこの雪崩は、極めて相性が良いということがご覧いただけるかと思います。
つまり、雪崩で使用される縦横格子のパリティ、斜め格子のパリティはそれぞれ完全に固定されており、パリティを決め打つことによって雪崩も作りやすくなるという一石二鳥という構図になっています。
(背景には、辺(枠)を使い切るという共通した理由が存在している為、これは必然的です)
このことから、パリティを決め打つことで得られる利点が、自由度が失われるという欠点よりも大きく上回ることが予想され、問題を解く上での大きなヒントを得ることが出来ます。
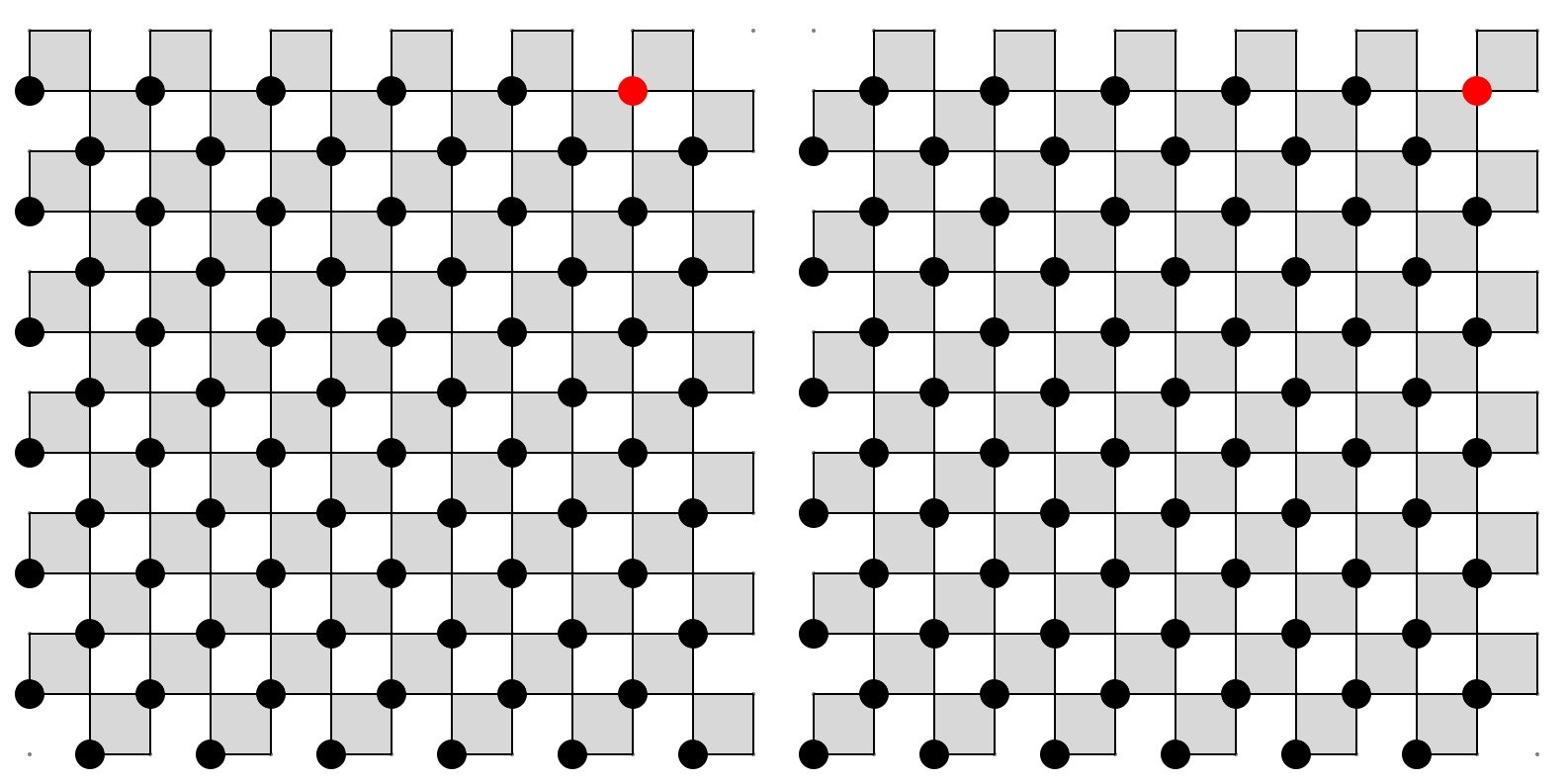
また、特にパリティを決め打つということと雪崩の関係の観点から言えば、「他方のパリティを全く使用しない」という別の面も非常に重要になってきます。
例えば、以下のような場合を考えてみます。
左が上手く雪崩を発生させられた場合、右が他方のパリティが混入してしまった場合の概念図です。
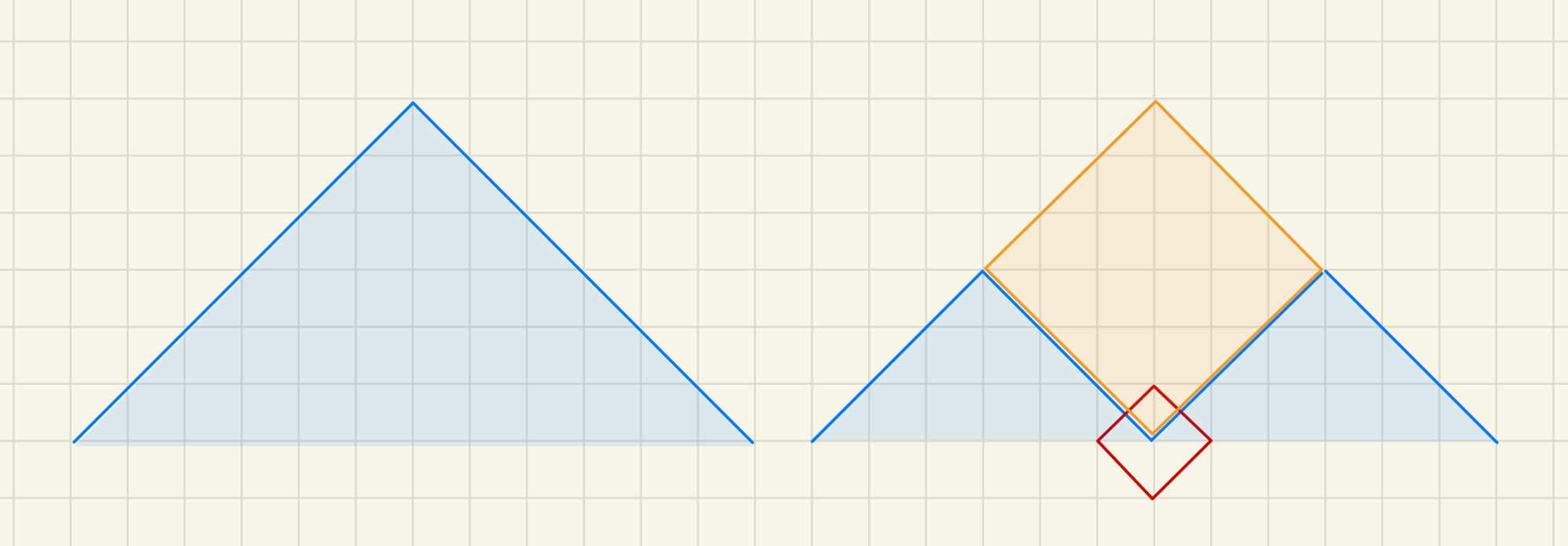
少し試せばすぐ分かることですが、一個でも他方のパリティを有する正方形を使用してしまうと、その時点で雪崩は完全にストップしてしまい、本来得られるはずだった得点が完全に失われてしまいます。特に、外側であればあるほどスコアの重みは大きかったので、その損失は絶大です。
局所的に見ていると、なぜ他とまったく同じ形の正方形が何万点もの損失につながるのか、ということは理解しづらいですが、パリティの混入という観点から見ればこれは自明で、後々ビームサーチをする上でも重要になってきます。
なお、縦横格子の方はパリティを変えても大丈夫です。
つまり、以下の別パターンも存在します。
そして同様に斜め格子についてもパリティは複数パターンあります。
しかし、実は以下の点には注意する必要があります。
前提A_5 雪崩には方向が存在する
先程の節で縦横格子と斜め格子はそれぞれ複数のパターンがあると述べましたが、実は斜め格子は縦横格子と決定的に違う点が存在しています。
実は斜め格子の扱いを決定することの方が縦横格子の扱いを決定するよりも基本的にはより重要です。
その理由は、雪崩には方向が存在するからです。
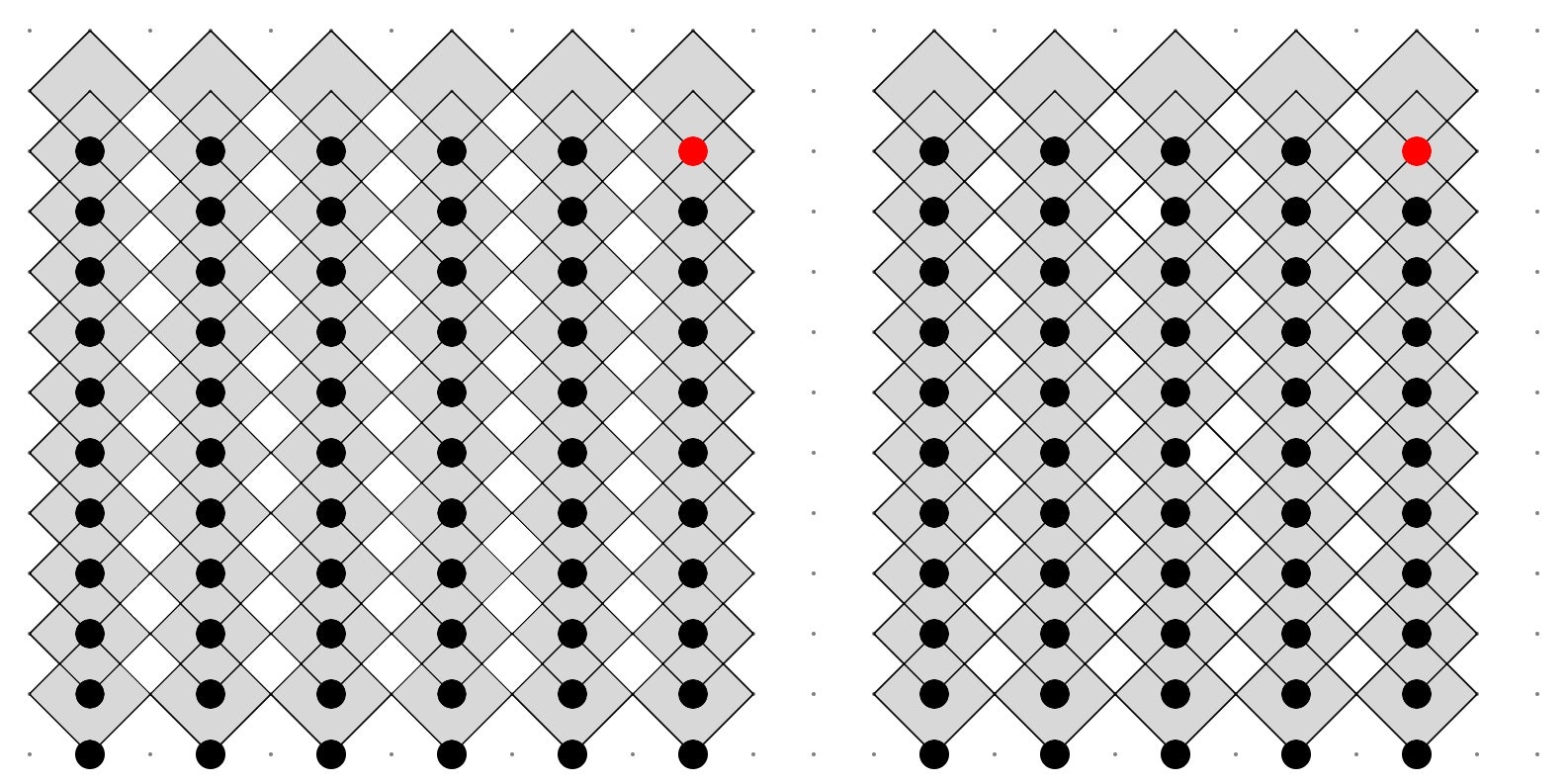
例えば、y軸に関するパリティを守ったかに思える以下のような図の場合、一見雪崩が発生してくれそうにも思えますが、よく見てもらえれば分かる通り、もう既に新たにおける点は(斜め格子では)一つもありません。
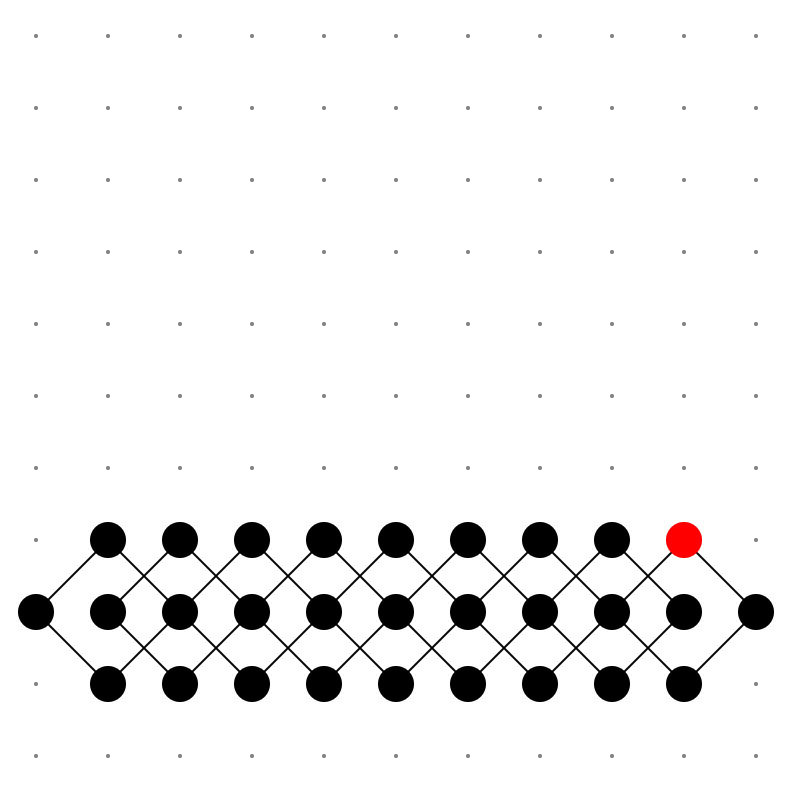
結局、雪崩が伸びる方向とは別の軸に関するパリティで斜め格子を制限しなければ、雪崩は発生しない、ということが分かります。
前提A_6 雪崩の方向を意識して、有効になる正方形を事前に列挙可能である
ここまでくれば前提Aはあと一歩です。
基本的には4方向すべてに雪崩を発生させた方が強いので、全方向に雪崩が発生できるよう、斜め格子のパリティに注意して格子を決定すると、例えば以下の通りになります。
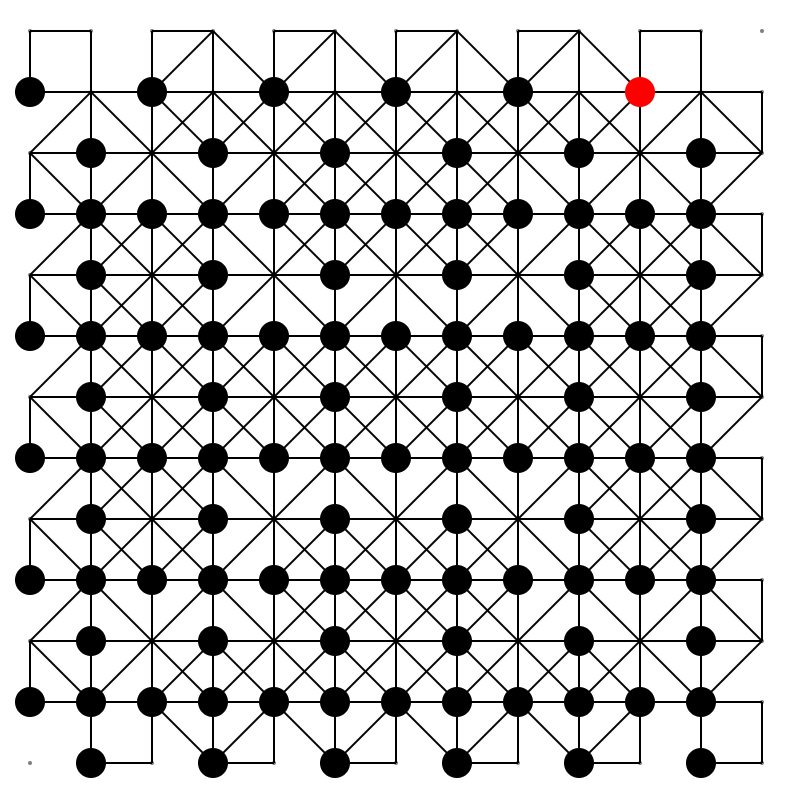
上の図では、図の上側、右側、下側、左側のどこに属しているか、ということを大まかな目安として斜め格子のパリティを切り替えており、このようにして、雪崩の方向に注意を払いながら有効になる正方形を事前に列挙することが出来ました。
以下、またまた独自の用語ですが、このように特定のパリティの組み合わせにおける有効な正方形のことをok_rectと呼ぶことにします。
同時に、パリティの嚙み合わせという語を導入します。斜め格子に関して、パリティを変更している境界線のような意味合いです。
先程の画像をよく見て頂ければ分かる通り、実はこのように列挙したok_rect達は、最密な敷き詰めではありません。異なるパリティを組み合わせて使用している為、前提A_2で述べたようにいくつかの正方形は失われてしまいます。
この失われる正方形というのが、パリティの噛み合わせそのものと言っても良いと思われます。
つまり、パリティの噛み合わせとは、雪崩の方向を変更させるために、一体どの正方形を放棄するのか、といった意味合いを持っています。
この噛み合わせ部分は、少なければ少ないほど多くの正方形を描けるので、あえて雪崩の向きを無視して噛み合わせ部分を減らすということも考えなくてはなりません。
(このように、パリティの嚙み合わせに関する議論は極めて重要なのですが、詳細は一旦省略します)
なお、これらok_rectを「事前に列挙可能である」ということは、それなりの意味を有します。
多くの場合、適当にやってしまうと、ある時点での合法手から一個取り出して採用すると、他の合法手も消えてしまうということが発生します。
これは同じ辺を共有している候補が複数含まれている場合、その内のどれか一つだけしか採用することが出来ないためです。
しかし、このok_rectに関しては最初から辺を共有せず、過去にどのような正方形を採用したかに依存しない列挙の仕方であるため、(上手く実装すれば)一回一回候補を更新する必要がなくなり、大幅な高速化が望めることになります。
実際、純粋なビームサーチを実装した場合、この合法手の更新が実行時間の9割を占めていたため、この高速化は割と本質的でした。
以上で前提Aは終了です。
…ところで、この前提Aというのは何か新規性のある内容なのでしょうか？
私以外で明確にこの雪崩などに言及していると感じた解法は（私の観測範囲だと）bowwowforeachさんとeijirouさん以外にあまりいらっしゃらず、他の方々は気付いている上で重要でないとスルーしているのか、他の方針で十分なので無視したのかどうなのかよく分かってないです。
少しは目新しさがある内容だといいのですが...
[追記]
その後、fuppy_kyoproさんやmakibishiさん、yUNIXさんもほぼ同様のことを考察されていることが分かりました。
やはり多くの方が気付いて考察されている事実のようですね。
こういったことに気付くことも、今回は重要だったのかも知れません。
では次に、あともう一つの前提Bを紹介していきます。
ビームサーチというメタヒューリスティックに関する前提
ここでは、問題自体とは少し離れて、メタヒューリスティック、つまり、問題を解く上での大まかな枠組みについて考えていきます。
先述の通り、私はビームサーチという手法を用いたので、それに関する汎用的なことを紹介していきます。
前提B_1 ビームサーチというメタヒューリスティック
広く知られた手法であるため、説明は下記リンクに任せます。
ご存知でない方は是非いくつかご覧になってください。
誤解を恐れず言えばビームサーチとは「幅のある貪欲」といった感じの手法で、この手法を用います。
前提B_2 chokudaiサーチというメタヒューリスティック
同様に、chokudaiサーチもビームサーチの亜種として広く知られています。
AtCoder社長のchokudaiさんによる手法です。
こちらも下記リンクを以って説明とさせて頂きます。
なお、普通にchokudaiサーチを使うとメモリを大量に使用するので、ガベージコレクションなどに時間がかかることがあります。
このような場合、ご本人のツイートにあるような対処をとるか、
あるいは、c++ではquick_exitを使うと良いと思われます。
私はこちらを今回採用しました。
しかし、実を言うと、私の解法におけるchokudaiサーチの得点に対する寄与は5%にもなりません。
chokudaiサーチの利点の一つに実行時間の管理が楽というのがあり、どうしてもビーム幅次第で時間が余ってしまうのを誤魔化すために採用した苦肉の策のようなものです。
なので、今回に関してはそこまで重要ではないです。
前提B_3 ZobristHashによる重複盤面の除去
さて、これまでに紹介した前提で私の方針が既におよそ分かった方も多いかと思われますが、これを愚直に実装しても、実は単なる貪欲とほぼ変わらない結果が出てしまいます。
その理由がビームサーチにおける多様性の欠如です。
具体例を挙げます。
長方形A、長方形B、長方形Cという3つの長方形がそれぞれ同時に採用できるとしましょう。
この時、この問題では「長方形を適用する順序」はあるものの、最終的に評価されるのは「結果となる盤面」だけなので、
- 長方形A→長方形B→長方形C
- 長方形A→長方形C→長方形B
- 長方形B→長方形A→長方形C
- 長方形B→長方形C→長方形A
- 長方形C→長方形A→長方形B
- 長方形C→長方形B→長方形A
の6パターンはそれぞれ別の状態とカウントされてしまいます。
このような長方形が4つ5つと増えていけば組み合わせ爆発が起こって、ビーム幅を増やしても、同じような状態ばかりを保持することになってしまい、これは望ましくありません。
このような問題に対処する一般的な手法にZobristHashによる重複除去というのが挙げられます。
簡単に言うと、盤面をxorでハッシュ化して、同じハッシュの状態を一つしか持たないとする手法です。
AHC011でも使用されている方がいらっしゃったので、割と汎用性のある手法だと思います。
このような工夫などを凝らすことで、ビームサーチに多様性を持たせることが出来ます。
(そしてこれが私がコンテスト後半に最も注力した事柄です。この点は感想にて後述します)
前提B_4 「確実に前進」という重要キーワード
長い前提の列挙もこれで最後です。そして、最後にして恐らく最も重要なことです。
突然ですが、皆さんはこちらの記事をご存じでしょうか。正直私のこの記事より100倍くらい有用なことが書いてあります。
この記事で言われている重要なことに、
遷移を設計する際に僕が指針としている考えは、確実に前進です。
ということがあります。
私はこのことを、探索すべきゲームなどに対して、操作をそのままビームサーチの合法手として据えるのではなく、いくつかの手をまとめたり、明らかに悪い手を最初から除いたりする事で、所謂ゴミ状態を削減し、より効率的にビームを打つようにしようということだと解釈しています。
今回も、この確実に前進ということを意識すると上手く行きました。
具体的には、前提Aで述べた本問の諸性質をうまく反映させることを考えます。
では、以下に解法のまとめを書きます。
解法まとめ
-
縦横格子、斜め格子のパリティに関して、合計16個のパターンを列挙します。
-
これら16パターンを初期状態として、ビームサーチを打ちます。最初の20ターンだけは、多様性確保の為、評価関数として以下の二通りを用いました。
(これ自体にあまり深い意味はなく、乱数も多様性確保の為です)- $(描かれたokrectの数)^{0.25}\times(生のスコア)\times([0.9,1.1]の範囲の乱数)$
- $(描かれたokrectの数)\times([0.9,1.1]の範囲の乱数)$
その後は生のスコアをそのまま使用しました。
-
確実に前進ということを意識しながら、ビームサーチにおける遷移に以下のようなルールを設けます。
- 基本的に遷移は非ok_rectをメインで考えます。
- 非ok_rectの長方形を適用した後、新たに合法となったok_rectを必ず全て適用させるようにします。(確実に前進の最たるポイントです。これによってゴミ状態を出来る限り削減します。)
- なお、この時パリティの嚙み合わせの都合上、斜め格子の方が縦横格子よりも重要になるため、dequeを用いて、斜め格子は前方に、縦横格子は後方に追加することで、優先的に縦横格子を使用し、斜め格子は温存します。そして、候補の更新を出来るだけ遅延させ、更新回数を減らします。
- ZobristHashによって重複が発覚したら遷移させません。
- 多様性確保のため、20ターンまでは、評価関数の値に関係なく、必ず各パターン最低10個は存在するように調整します。
-
これらが終わったのち、まだ時間が余っているようであれば、先程までに確定した最善のパターンでchokudaiサーチをします。基本的には上と同じですが、今度は必ずしもok_rectを全て適用させなくてもよいと制限を緩めています。
このようにすると、暫定スコアで64,113,260点の20位、システムテストで2,514,100,162点の24位になることが出来ます。
(確実にパラメータ調整をミスっていたので、システムテストはちょっと下振れです…)
以上で本解説記事のメインは終了です。お読みいただきありがとうございました。
不明点や間違っている点があれば教えて頂けると幸いです。
以下、興味のある方はあと少しだけお付き合い下さい。
感想1
101回いいねしました。chokudaiサーチによるAHC優勝者が見てみたいです。
尤も、ビームサーチ系がボコられているのは、純粋に問題との相性が悪いだけな気もしますが…
感想2
以下は解説記事ではなく、参加記のような色が強い反省です。
今回は明らかに焼き鈍し系が強かったですが、これは一体何故かということを私はずっと考えていました。
いくつもこれまでに述べてきた議論や実装に穴があることは分かっていますが、それでも最も後悔があるとすればパリティの嚙み合わせです。焼き鈍しは基本的に全然考えなかったものの、ここで焼き鈍しがちらと頭によぎってはいたので、ここで方針ミスに気が付くべきでした。
コンテストの後半は多様性の確保に注力したとは先述の通りですが、それをやってもやっても思うようにスコアの上昇につながりませんでした。
単純に多様性を確保するだけでは、事前にok_rectが決められている為、柔軟なパリティの嚙み合わせを実現させることが困難です。
これが雪崩の発生を止めていることまでは分かっていたので、ここで方針転換に踏み切れなかったのは凄く悔しいです。
尤も、どうやらWLeiteさんのstatisticsによれば、私の最大の反省点はSparseな場合(つまり、雪崩と無縁な場合)のようです。
ただ、これに気付くのはちょっと無理みがありますね…
正直全く気が付きませんでした。
自己ベストは管理してそれとの比較は常に表示していましたが、それでも気がつかなかったので、ここはちょっと仕方ないと思っている節があります。
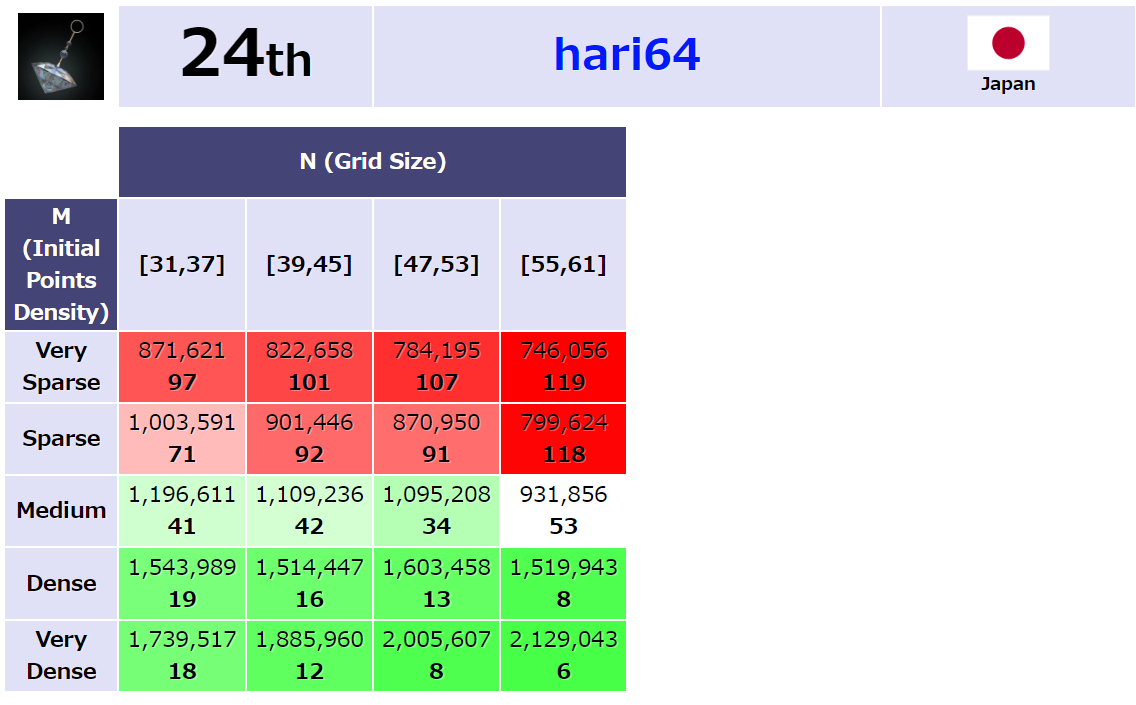
やはり、自分が最も考えていたことの延長線上に、局所的な更新に強い焼き鈍しという解が見えていたので、そこまで突っ切れていたらなと思ってしまいます。
色々反省点はありますが、次回のAHCが今から楽しみです。
ここまでお読みいただきありがとうございました。
最後にestieさんに感謝を込めてリンクを置いておきます。
楽しいコンテストをありがとうございました。