関数の最小値(最大値)を求める事の重要性
「ある関数の最小値(最大値)とそのときのパラメータを求める」という、いわゆる最小化(最大化)問題というのはとても重要な問題だったりします。
これまで計算科学において、例えば計算物理学では、エネルギーを最小化して相転移などの物理現象を解析する、といった事が盛んに行われてきました。
ところが最近では、機械学習のためにもこの手の問題が考えられているようです。
その理由は、機械学習では、損失関数と呼ばれる関数を最小化することでニューラルネットワークを構成するパラメータの決定(学習)を行うからです。そして、そこで得たパラメータを用いて画像認識や音声認識などデータの分類や推測を行います。
このように、これまで計算科学の分野でのみ考えられてきた関数の最小化(最大化)問題というのは、情報科学の進歩によってさらに多方面の分野に広がりを見せていて、今まで以上に重要度が増しているのです。
ところで、最大値を求めるという問題は、関数の符号を反転させれば最小値を求める問題へと帰着されます。
というわけで、これ以降は、関数の最小値を求める事だけを考えるとし、最小値を求める数値的手法とそのベンチマーク結果を紹介します。
勾配降下法(最急降下法)
関数$f(x_1,x_2,...,x_m)$の最小値を求める最もシンプル、かつ、実装が容易な方法は勾配降下法(最急降下法)です。
計算の原理は至って簡単で「斜面の傾きを利用して標高の低い方向へと進んでいく」というものです。
具体的には、なんらかの方法によって関数$f(x_1,x_2,...,x_m)$の微分を計算し、次の表式によって変数$x_1,x_2,...,x_m$の更新を反復的に行うという手法です。
x_{i}^{(n+1)} = x_{i}^{(n)} - \eta \frac{\partial f(x_1^{(n)},x_2^{(n)},...,x_m^{(n)})}{\partial x_i}
\left| x_{i}^{(n+1)} - x_{i}^{(n)} \right| < \varepsilon (収束条件)
ここで、$x_{i}^{(n)}$は$n$回目の反復計算によって得られた$i$番目の変数を表し、$n$回目と$n+1$回目の計算結果が$\varepsilon$未満となったとき、値が収束して最小値が求まったものと判断し、計算を終えます。
$\eta$は学習係数と呼ばれる正のパラメータで、計算を行う人間が適当に値を調整する必要があります。
式を見てもらえば解りますが、傾きの符号の逆方向、つまり、谷の方向に向かって変数を更新してますよね。
このようにして、$n$回目の計算で得られた座標と傾きを使い、さらに良いであろう$n+1$回目の結果を得るわけです。
勾配降下法による計算例
例として次の関数の最小値と座標を求めることで勾配降下法をベンチマークをしてみます。
f(x_1,x_2) = \frac{1}{20}(x_{1}-8)^{2} +(x_{2}+5)^2 \tag{1}
なお、ここでは初期値として$x_1^{(0)}=-10,x_2^{(0)}=10$と選び、収束条件は$\varepsilon < 10^{-6}$としました。
こんなもの数値計算するまでもなく最小値は$0$で、そのときの座標は$x_1=8,x_2=-5$なのですが、勾配降下法が一体どんなものなのか確認するために性質のよく解った関数を例として選びました。
まず、勾配降下法では適当な学習係数$\eta$を選択しなければなりません。
$\eta$が小さすぎると少ししか値が更新されないため収束が遅く、逆に大きすぎると谷を飛び越えて明後日の方向に更新が行われてしまうからです。
次に示すグラフは勾配降下法の計算によって得た、学習係数$\eta$(横軸)と値が収束するまでの更新の回数(縦軸)の関係を示したものです。
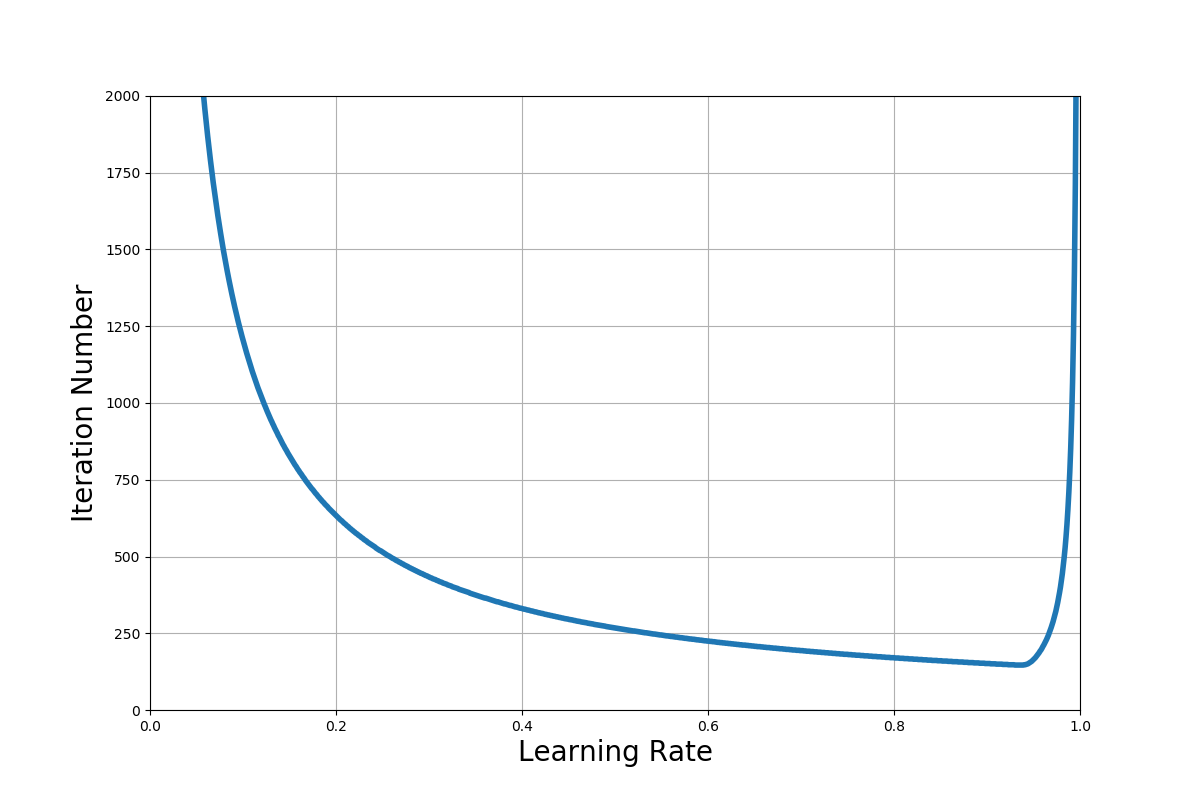
この図より、$\eta<1$の範囲で収束することが確認できますね。
なお、収束に必要な更新回数の最小値は$\eta = 0.93$のときの147回でした。
それでは一体どのようにして値が更新されているのか確認してみましょう。
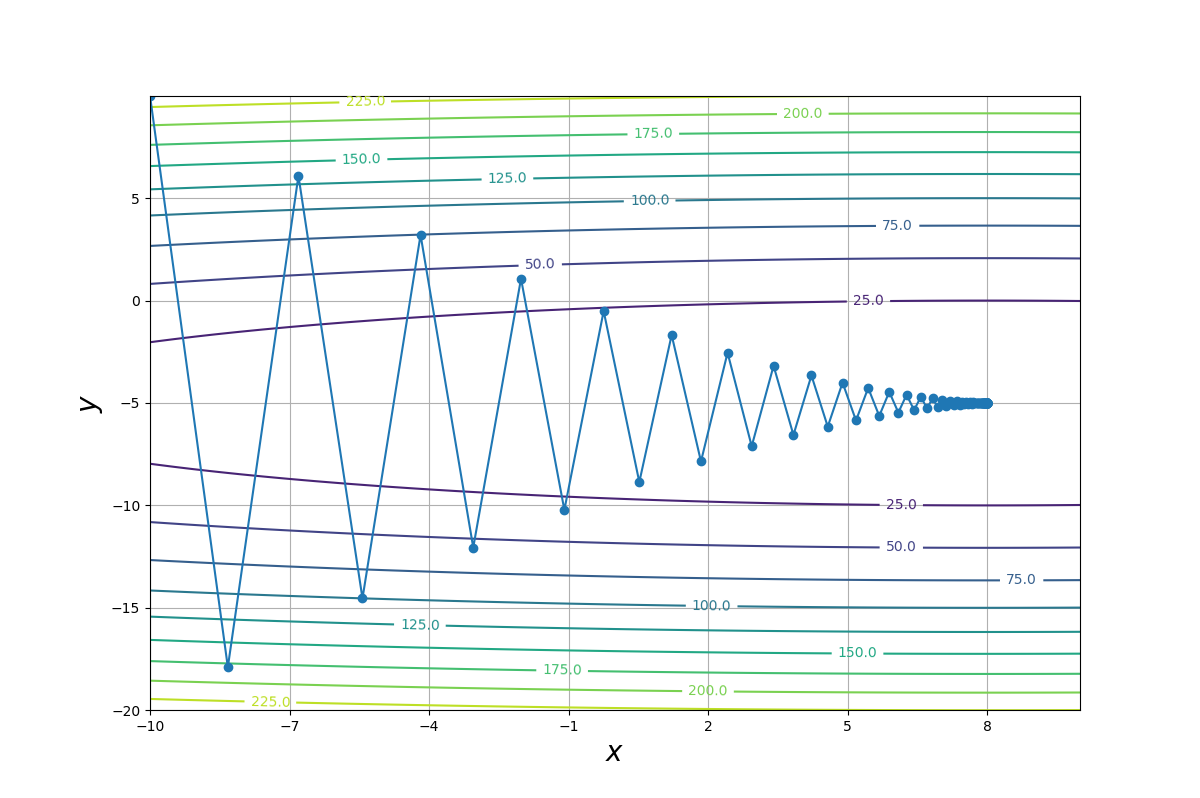
下の図は、学習係数を最適にチューニングしたとき$(\eta=0.93)$の、反復計算によって更新されてゆく$x_1^{(n)},x_2^{(n)}$の軌跡と$f(x_1,x_2)$の等高線を$x$-$y$平面上に示したものです。
$x_1^{(n)},x_2^{(n)}$は$f(x_1,x_2)$の最小値に向かって正しく進んではいますが、かなりジグザグに移動していることが解りますね。
このグラフを見る限り、あまり効率的ではない進み方をしているとは感じないでしょうか?
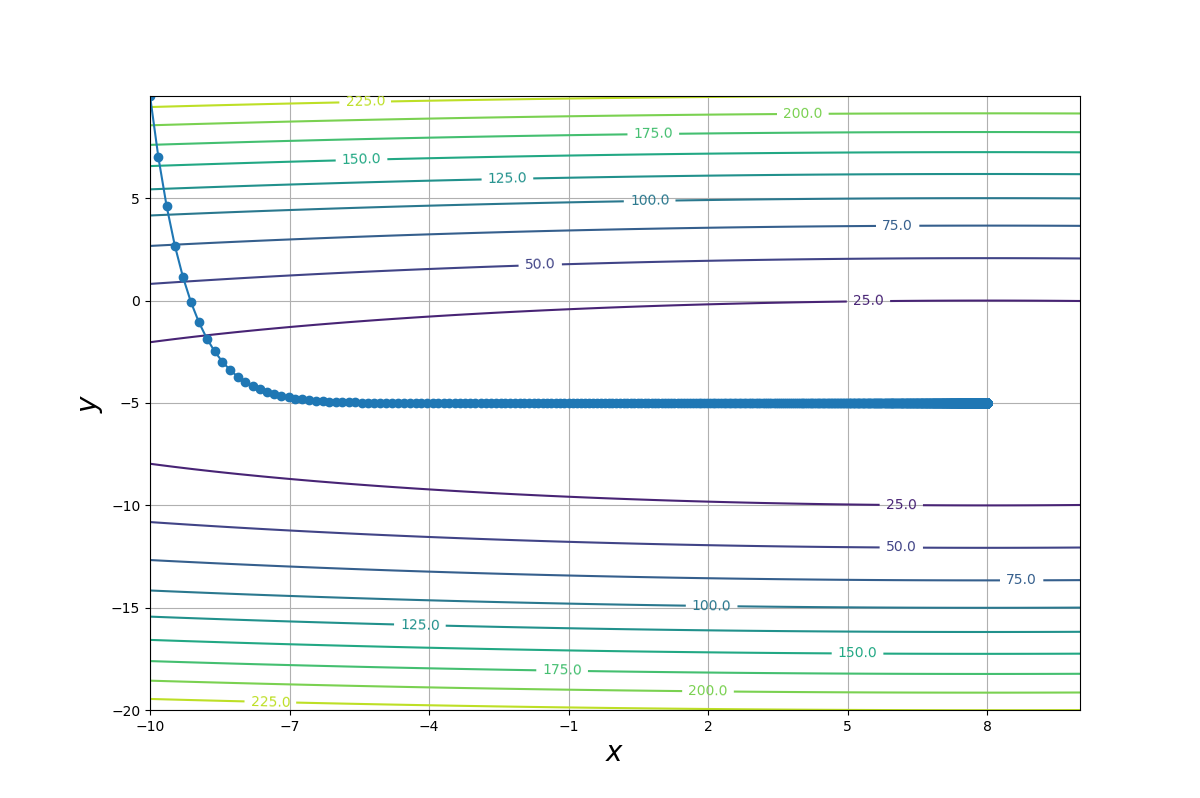
なお、学習係数が小さい$(\eta =0.1)$場合は次のような軌跡になります。
この場合、勾配が最も急な方向(等高線に垂直な方向)に沿って値が更新されています。(勾配降下法が最急降下法とも呼ばれる所以はこれです。)
しかし、更新される値が小さいため収束が遅く、計算回数は多くなっているようです。
AdaGrad
これまで勾配降下法について見てきました。
関数の最小値を求めることができた一方、「更新の効率があまり良ろしくないのでは?」と感じたのも事実です。
そこで考え出されたのが次の表式で表されるAdaGradと呼ばれる手法です。
h_{i}^{(n+1)} =h_{i}^{(n)} + \left (\frac{\partial f(x_1^{(n)},x_2^{(n)},...,x_m^{(n)})}{\partial x_i} \right)^2
x_{i}^{(n+1)} = x_{i}^{(n)} - \frac{\eta}{\sqrt{h_i^{(n+1)}}} \frac{\partial f(x_1^{(n)},x_2^{(n)},...,x_m^{(n)})}{\partial x_i}
\left| x_{i}^{(n+1)} - x_{i}^{(n)} \right| < \varepsilon (収束条件)
ポイントは関数の微分を利用して$h_{i}^{(n)}$という因子を計算し、$x_{i}^{(n)}$を更新する際に用いるという点です。
そして学習係数$\eta$を$\sqrt{h_{i}^{(n)}}$で補正しているので、変数ごとに学習係数を調整しているとも見なせます。
しかし、それ以外は勾配降下法と変わりません。
また、$h_{i}^{(n)}$を計算するために必要な$f(x_1,x_2,...,x_m)$の微分は、勾配降下法でも必要となったものですから、AdaGradのために特別に用意する必要はありません。
しかしながら、結論から先に言えば、これだけの工夫で計算時間を圧倒的に短縮できます。
AdaGradによる計算例
勾配降下法同様に、(1)式で表される関数$f(x_1,x_2)$をAdaGradによって最小化するというベンチマークを行いました。
初期値と収束条件は勾配降下法のときと同じ$x_1^{(0)}=-10,x_2^{(0)}=10,\varepsilon < 10^{-6}$に設定し、$h_{i}^{(0)}=0$としました。
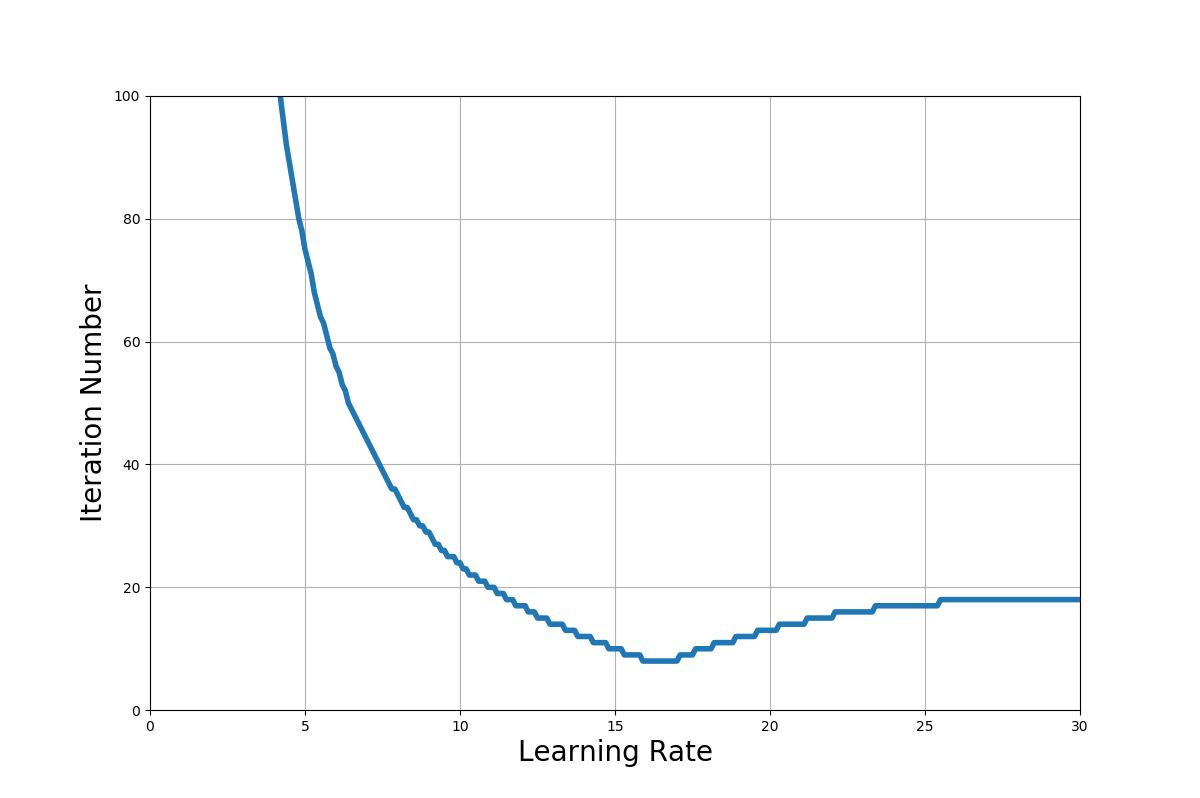
AdaGradによって求めた学習係数$\eta$と値が収束するまでに必要となった反復計算の関係を次の図に示します。
この図より、AdaGradを用いると$\eta>1$でも収束していることが確認できます。
また、学習係数$\eta = 15.9$に設定すれば、たったの8回計算しただけで値が収束するという結果が得られました。
これは勾配降下法と比べると歴然の差ですね!
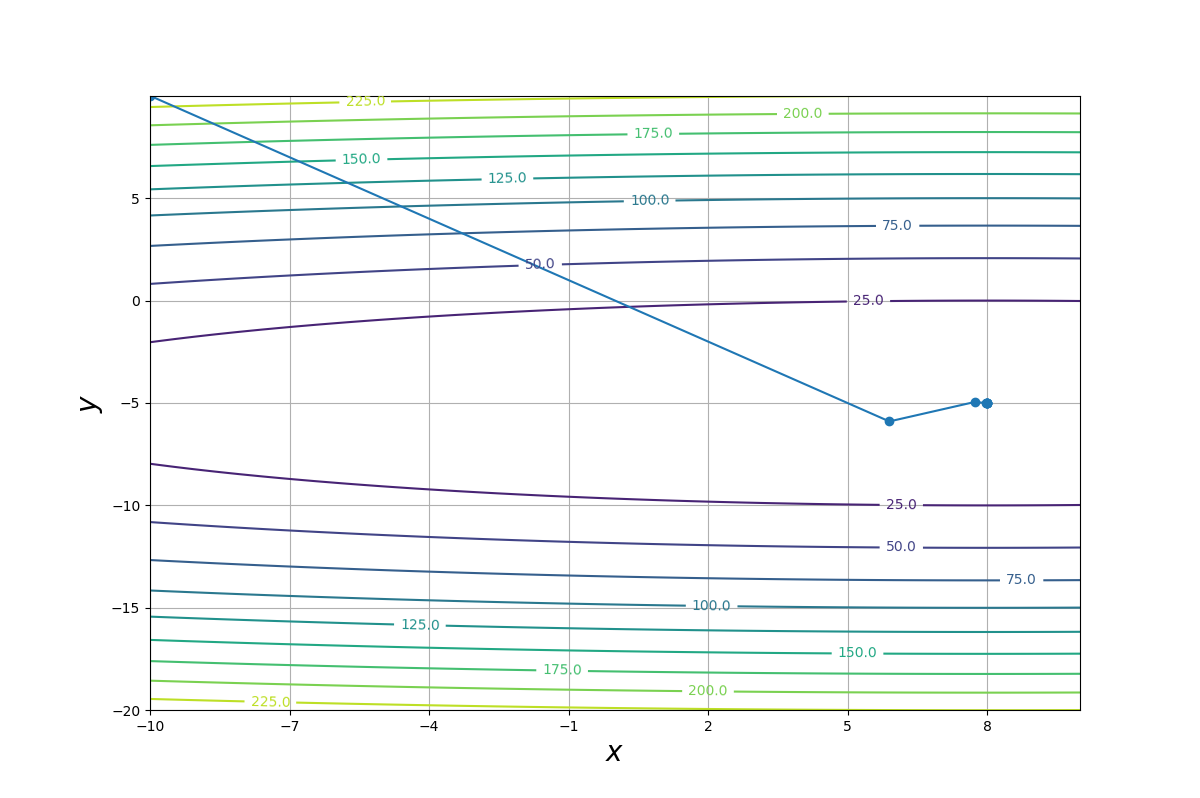
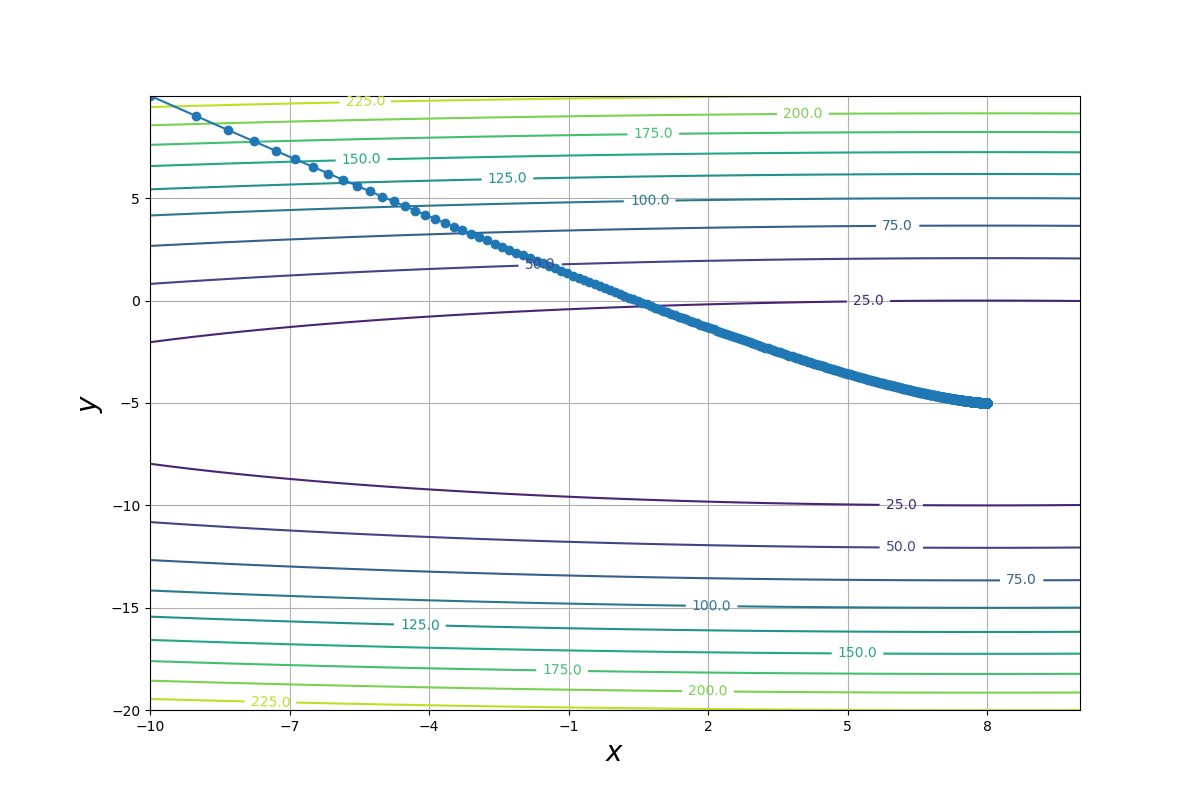
続いて、最適にチューニングした学習係数$(\eta = 15.9)$での$x$-$y$平面に描画した$x_1^{(n)},x_2^{(n)}$軌跡と$f(x_1,x_2)$の等高線を以下の図に示します。
最適にチューニングしたAdaGradでは1回目の計算でかなり解に近い値まで更新され、2回目以降の計算では解と殆ど変わらない値まで近づいています。
勾配降下法のようにジグザグな軌跡を描くということはないようです。
なお、学習係数が小さい場合$(\eta = 1)$の軌跡は次の図ようになります。
勾配降下法では斜面に最も急な方向に値を更新していましたが、AdaGradは目的地への最短経路に近い方向へに向かって値を更新しているように見えますね。
結論
AdaGradはすごい。
勾配降下法が実装できるなら、少しの工夫で出来るAdaGradも試してみる価値はあると思いました。