はじめに
状態空間モデルにおいて状態を逐次的に推定する有名な手法の1つにカルマンフィルタというものがあります。
カルマンフィルタなどを用いて出来る事・概要・手順・numpyを用いた行列実装をまとめてみました。
この記事の対象としている人
- 確率分布の計算はなんとなくわかる
- 状態空間の概念はなんとなくわかる
- カルマンフィルタはよく知らない
- numpyの行列実装の仕方を知りたい
カルマンフィルタで出来る事
カルマンフィルタを使うと、ノイズ混じりの観測データから、観測ノイズを取り除いた状態を逐次推定できます。
こんな感じです。
経済やマーケティングの文脈においては、時系列データの平滑化やトレンドの把握、少し先の予測などに使われます。
ある事象に対して、時点1から時点tまで時系列に沿って観測したデータ$y_{1:t}$があるとします。
例えば、DAU(Daily Active User, 1日あたりにログインしたユーザー数)を想定します。
DAUが以下のように分解出来るとします。
DAU = 状態(サービス内要因, サービス魅力度など) + 観測誤差(サービス外要因, 曜日変動やノイズなど) \\
観測誤差(サービス外要因) \sim N(0, \Sigma) \\
DAUの監視を通じて知りたいのは、時点tにおけるサービスの魅力度を表す状態$x_t$です。しかし、状態$x_t$そのものを直接観測する事は出来ず、観測出来るDAUはサービス外の要因が混じっています。なので、DAU観測データ$y_{1:t}$からサービス外の要因を取り除き、状態$x_t$を推定したいです。
そこで、フィルタリングや予測、平滑化を行います。
フィルタリング、予測、平滑化の違い
時点1から時点tまでの観測データ$y_{1:t}$を元に、ある時点の状態$x_{t'}$を推定します。つまり、$p(x_{t'} | y_{1:t})$を求めます。
より正確には、観測データが手元にあるときの時点tの状態$x_t$確率分布$p(x_{t'} | y_{1:t})$を求め、その平均や分散を求めます。
ここで、
- t' < t, つまり時点tまでの観測値を元に過去の時点の状態$x_{t'}$を推定する場合、平滑化
- t' = t, つまり時点tまでの観測値を元に現在の時点の状態$x_{t'}$を推定する場合、フィルタリング
- t' > t, つまり時点tまでの観測値を元に未来の時点の状態$x_{t'}$を推定する場合、予測
という違いがあります。
例えば、過去のトレンドを知りたいときは平滑化を行ってもよいですし、現在のトレンドをリアルタイムに知りたければ、最新時点のデータが入ってくる度にフィルタリングを行えばよいでしょう。
カルマンフィルタについて
カルマンフィルタ、カルマン予測、カルマン平滑化の順に説明します。
前提
まず、以下のような状態空間モデルを想定します
状態方程式: x_t = G_t x_{t-1} + w_t \\
観測方程式: y_t = F_t x_t + v_t \\
状態ノイズ: w_t \sim N(0, W_t) \\
観測ノイズ: v_t \sim N(0, V_t)
$x_t, w_t$: p×1ベクトル
$G_t, W_t$: p×p行列
$F_t$: 1×pベクトル
$y_t, v_t, V_t$: スカラー
状態$x$は、時点tが増えるにつれ係数$G$がかかり、状態が遷移していきます。
状態が遷移する度に、正規分布に従うノイズ$w$が混ざります。
時点tの観測値$y_t$は、観測方程式に従って求められます。
観測値$y_t$には、正規分布に従う観測ノイズ$v$が混ざります。
$G_t, F_t, W_t, V_t$は既知であるとします。
カルマンフィルタの概要
カルマンフィルタは、時点tまでの観測値$y_{1:t}$から時点tの状態$x_t$を逐次的に効率よく求める手法です。
観測値から観測ノイズを取り除いた状態を推定するので、フィルタリングと呼ばれます。
時点tまでの観測値$y_{1:t}$の情報を元に時点tの状態$x_t$を推測するフィルタリング分布$p(x_t | y_{1:t})$を逐次的に求めたいです。
具体的には、時点毎のフィルタリング分布を仮定し、そのパラメータを逐次的に求めたいです。
そのために、以下の3つの分布を設定します。
フィルタリング分布: p(x_t | y_{1:t}) = N(m_t, C_t) \\
一期先予測分布: p(x_t | y_{1:1-t}) = N(a_t, R_t) \\
一期先予測尤度: p(y_t | y_{1:t-1}) = N(f_t, Q_t) \\
フィルタリング分布は時点tまでの観測値$y_{1:t}$を元に時点tの状態$x_t$を発生させる分布
一期先予測分布は時点t-1までの観測値$y_{1:t-1}$を元に時点tの状態$x_t$を予測する分布
一期先予測尤度は時点t-1までの観測値$y_{1:t-1}$を元に時点tの観測値$y_t$を予測する関数
一期先予測分布$p(x_t | y_{1:t-1})$は、観測値$y_t$を観測する前に予測したフィルタリング分布$p(x_t | y_{1:t})$のようなものです。
フィルタリング分布と一期先予測分布はどちらも$x_t$を発生させる確率分布になっています。
最後の関数が尤度と名付いているのは、恐らくこの関数が観測された$y_{1:t}$から尤もらしいパラメータ$m_t, C_t$を推測するために使われるからだと思われます。
確率"分布"(確率密度関数)は固定したパラメータからある値が発生する確率を求めるのに対し、"尤度"(尤度関数)は観測されたデータ(固定された値)を発生させたパラメータがある値だとどれくらい尤もらしいかを返す関数です。
時点tにおけるパラメータ$\Theta_t = { m_t, C_t, a_t, R_t, f_t, Q_t }$を、時点t-1のフィルタリング分布パラメータ$m_{t-1}, C_{t-1}$と観測値$y_t$を用いて求めます。
カルマンフィルタの手順
過去の観測値$y_{1:t-1}$から1期先予測分布(予測値に基づくフィルタリング分布)を計算して、その後に観測された$y_t$を用いて1期先予測分布のパラメータを修正していくイメージです。
1期先予測分布$p(x_t|y_{1:t-1})$を計算・予測
↓
データ$Y_t=y_t$を観測
↓
$y_t$の情報を元にフィルタリング分布$p(x_t|y_{1:t})$へ修正
この計算を観測したい時点まで繰り返します。
初期状態のフィルタリング分布のパラメータ$m_0, C_0$を設定します。
以下の計算をT回繰り返します。
1 時点tの一期先予測分布$p(x_t | y_{1:t-1})$のパラメータ
a_t = G_t m_{t-1} \\
R_t = G_t C_{t-1} G_t^T + W_t
2 時点tの一期先予測尤度$p(y_t | y_{1:t-1})$のパラメータ
f_t = F_t a_t \\
Q_t = F_t R_t F_t^T + V_t
3 時点tのカルマンゲイン
K_t = R_t F_t^T Q_t^{-1}
4 時点tの状態($x_t$を発生させるフィルタリング分布のパラメータ)の更新
m_t = a_t + K_t(y_t - f_t) \\
C_t = (I - K_t F_t) R_t
# コードにするとこんな感じ
def kalman_filter(m, C, y, G=G, F=F, W=W, V=V):
"""
Kalman Filter
m: 時点t-1のフィルタリング分布の平均
C: 時点t-1のフィルタリング分布の分散共分散行列
y: 時点tの観測値
"""
a = G @ m
R = G @ C @ G.T + W
f = F @ a
Q = F @ R @ F.T + V
# 逆行列と何かの積を取る場合は、invよりsolveを使った方がいいらしい
K = (np.linalg.solve(Q.T, F @ R.T)).T
# K = R @ F.T @ np.linalg.inv(Q)
m = a + K @ (y - f)
C = R - K @ F @ R
return m, C
カルマン予測の概要・手順
カルマン予測は、t+k時点予測分布$p(x_{t+k} | y_{1:t})$を求める手法です。
基本的な概念はカルマンフィルタと変わりません。
カルマンフィルタは
- 一期先予測分布$p(x_t | y_{t-1})$を計算
- データ$y_t$を元にフィルタリング分布$p(x_t|y_{1:t})$へ修正
という流れを辿っていましたが、未来のデータは観測出来ません。そこで
- 最新時点tのフィルタリング分布$p(x_t | y_{1:t})=p(x_{t+0} | y_{1:t})$を準備、時点tにおける0期先予測分布とする
- $p(x_t | y_{1:t})$を用いてt+1時点の一期先予測分布$p(x_{t+1} | y_{1:t})$を計算
- $p(x_{t+1} | y_{1:t})$を用いてt+2時点の一期先予測分布$p(x_{t+2} | y_{1:t})$を計算
...
というように、観測データによる修正をせずひたすら予測分布の計算を繰り返します。カルマンフィルタと同じ計算式です。
時点tでの0期先予測分布$a_t(0)=m_t, R_t(0)=C_t$を元に、時点t+k, k期先予測分布の平均$a_t(k)$, 分散$R_t(k)$をk=1~kまで逐次的に計算します
a_t(k) = G_{t+k} a_t(k-1) \\
R_t(k) = G_{t+k} R_t(k-1) G_{t+k}^T + W_{t+k}
# 一期先予測分布を連続して求めるだけ
def kalman_prediction(a, R, G=G, W=W):
"""
Kalman prediction
"""
a = G @ a
R = G @ R @ G.T + W
return a, R
カルマン平滑化の概要・手順
カルマン平滑化は、時点tの平滑化分布
p(x_t | y_{1:T}) = N(s_t, S_t)
を求める手法です。(t < T)
カルマンフィルタを時点Tまで計算したとします。
カルマン平滑化は、時点tのフィルタリング分布$p(x_t | y_{1:t})$を、時点t+1の平滑化分布$p(x_{t+1} | y_{1:T})$で補正します。
これにより、トレンドはより滑らかになります。
手順(RTSアルゴリズム)
0 時点t+1での平滑化分布: $s_{t+1}, S_{t+1}$を準備(t=Tのときは時点tのフィルタリング分布を使用)
1 時点tの平均化利得を計算
A_t = C_t G_{t+1}^T R_{t+1}^{-1}
2 時点tの平滑化分布のパラメータを計算
s_t = m_t + A_t(s_{t+1} - a_{t+1}) \\
S_t = C_t + A_t(S_{t+1} - R_{t+1})A_t^T
# カルマン平滑化
# 固定区間平滑化を行う
# 時点Tまでのカルマンフィルタリングが一旦完了しているものとする
# aとRの計算は、カルマンフィルタリングの計算時に格納したものを使った方が、計算効率は良さそう
def kalman_smoothing(s, S, m, C, G=G, W=W):
"""
Kalman smoothing
"""
# 1時点先予測分布のパラメータ計算
a = G @ m
R = G @ C @ G.T + W
# 平滑化利得の計算
# solveを使った方が約30%速くなる
A = np.linalg.solve(R.T, G @ C.T).T
# A = C @ G.T @ np.linalg.inv(R)
# 状態の更新
s = m + A @ (s - a)
S = C + A @ (S - R) @ A.T
return s, S
実装
自作関数の定義だけ上に書いたものを使います。
ライブラリのインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from tqdm import tqdm_notebook as tqdm
np.random.seed(1234)
pd.set_option('display.max_columns', None)
sns.set_style('darkgrid')
%matplotlib inline
仮想データ
一番簡単な例として、ランダムウォークを想定します。
これは、ローカルモデルの一種です。
x_t = x_{t-1} + w_t \\
y_t = x_t + v_t \\
w_t \sim N(0, 1) \\
v_t \sim N(0, 10) \\
観測時点Tは100, 予測時点は5, 初期状態は100とします
G = np.array([[1]])
F = np.array([[1]])
W = np.array([[1]]) # 恣意的に与える必要がある
V = np.array([[10]]) # 上に同じ
T = 100
K = 5
x0 = 100
w = np.random.multivariate_normal(np.zeros(1), W, T+K)
v = np.random.multivariate_normal(np.zeros(1), V, T+K)
x = np.zeros(T+K)
y = np.zeros(T+K)
x[0] = x0 + w[0]
y[0] = x[0] + v[0]
for t in range(1, T+K):
x[t] = x[t-1] + w[t]
y[t] = x[t] + v[t]
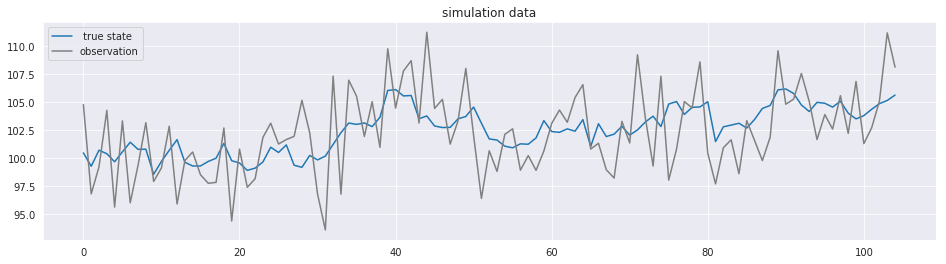
fig, ax = plt.subplots(figsize=(16, 4))
sns.lineplot(np.arange(T+K), x, ax=ax, label=" true state")
sns.lineplot(np.arange(T+K), y, color="gray", ax=ax, label="observation")
ax.set_title("simulation data")
ax.legend()
plt.show()
パラメータ設定
# 初期状態のフィルタリング分布のパラメータ
m0 = np.array([[0]])
C0 = np.array([[1e7]])
# 結果を格納するarray
m = np.zeros((T, 1))
C = np.zeros((T, 1, 1))
a_pred = np.zeros((K, 1))
R_pred = np.zeros((K, 1, 1))
s = np.zeros((T, 1))
S = np.zeros((T, 1, 1))
実行
# カルマンフィルター
for t in range(T):
if t == 0:
m[t], C[t] = kalman_filter(m0, C0, y[t:t+1])
else:
m[t], C[t] = kalman_filter(m[t-1:t], C[t-1:t], y[t:t+1])
# カルマン予測
for t in range(K):
if t == 0:
a = G @ m[T-1:T]
R = G @ C[T-1:T] @ G.T + W
a_pred[t] = a
R_pred[t] = R
else:
a_pred[t], R_pred[t] = kalman_prediction(a_pred[t-1], R_pred[t-1])
# カルマン平滑化
for t in range(T):
t = T - t - 1
if t == T - 1:
s[t] = m[t]
S[t] = C[t]
else:
s[t], S[t] = kalman_smoothing(s[t+1], S[t+1], m[t], C[t])
結果
$Z_{0.05/2} \fallingdotseq 1.96$より、標準偏差に1.96を掛けたものを95%区間とします。
カルマンフィルタリング(t<=100)とカルマン予測(t>100)の結果をプロットします。
upper = 115
lower = 85
legend_loc = "lower left"
fig, axes = plt.subplots(nrows=3, figsize=(16, 12))
sns.lineplot(np.arange(T+K), x, ax=axes[0], label="true state")
sns.lineplot(np.arange(T+K), y, color="gray", ax=axes[0], label="observation")
sns.lineplot(np.arange(T), m.flatten(), color="red", ax=axes[0], label="kalman filter + prediction")
axes[0].plot(np.arange(T), (m - 1.96 * C[:,:,0]**(1/2)).flatten(), alpha=0.3, color='gray', label=".95 interval")
axes[0].plot(np.arange(T), (m + 1.96 * C[:,:,0]**(1/2)).flatten(), alpha=0.3, color='gray')
axes[0].plot(np.arange(T, T+K), a_pred.flatten(), color='red')
axes[0].plot(np.arange(T, T+K), (a_pred - 1.96 * R_pred[:,:,0]**(1/2)).flatten(), alpha=0.3, color='gray')
axes[0].plot(np.arange(T, T+K), (a_pred + 1.96 * R_pred[:,:,0]**(1/2)).flatten(), alpha=0.3, color='gray')
axes[0].axvline(100, color="black", linestyle="--", alpha=0.5, label="left: filtering, right: prediction")
axes[0].set_ylim(lower, upper)
axes[0].legend(loc=legend_loc)
axes[0].set_title("Kalman Filter + Prediction")
sns.lineplot(np.arange(T+K), x, ax=axes[1], label="true state")
sns.lineplot(np.arange(T+K), y, color="gray", ax=axes[1], label="observation")
sns.lineplot(np.arange(T), s.flatten(), color="green", ax=axes[1], label="kalman smoothing")
axes[1].plot(np.arange(T), (s - 1.96 * S[:,:,0]**(1/2)).flatten(), alpha=0.3, color='gray', label=".95 interval")
axes[1].plot(np.arange(T), (s + 1.96 * S[:,:,0]**(1/2)).flatten(), alpha=0.3, color='gray')
axes[1].axvline(100, color="black", linestyle="--", alpha=0.5, )
axes[1].set_ylim(lower, upper)
axes[1].legend(loc=legend_loc)
axes[1].set_title("Kalman Smoothing")
# sns.lineplot(np.arange(T+K), x, ax=axes[2], label="true state")
sns.lineplot(np.arange(T+K), y, color="gray", ax=axes[2], label="observation")
sns.lineplot(np.arange(T), m.flatten(), color="red", ax=axes[2], label="kalman filter")
sns.lineplot(np.arange(T), s.flatten(), color="green", ax=axes[2], label="kalman smoothing")
axes[2].axvline(100, color="black", linestyle="--", alpha=0.5)
axes[2].set_ylim(lower, upper)
axes[2].legend(loc=legend_loc)
axes[2].set_title("Kalman filter vs kalman smoothing")
plt.show()
print("カルマンフィルタリングの分散の平均: {:.3f}".format(C.mean()))
print("カルマン平滑化の分散の平均: {:.3f}".format(S.mean()))

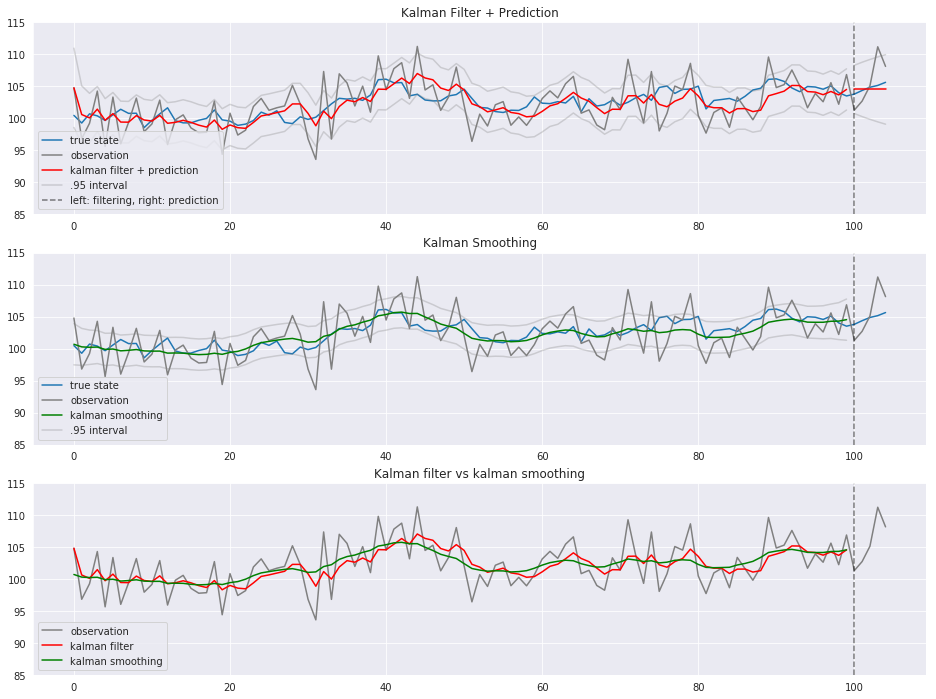
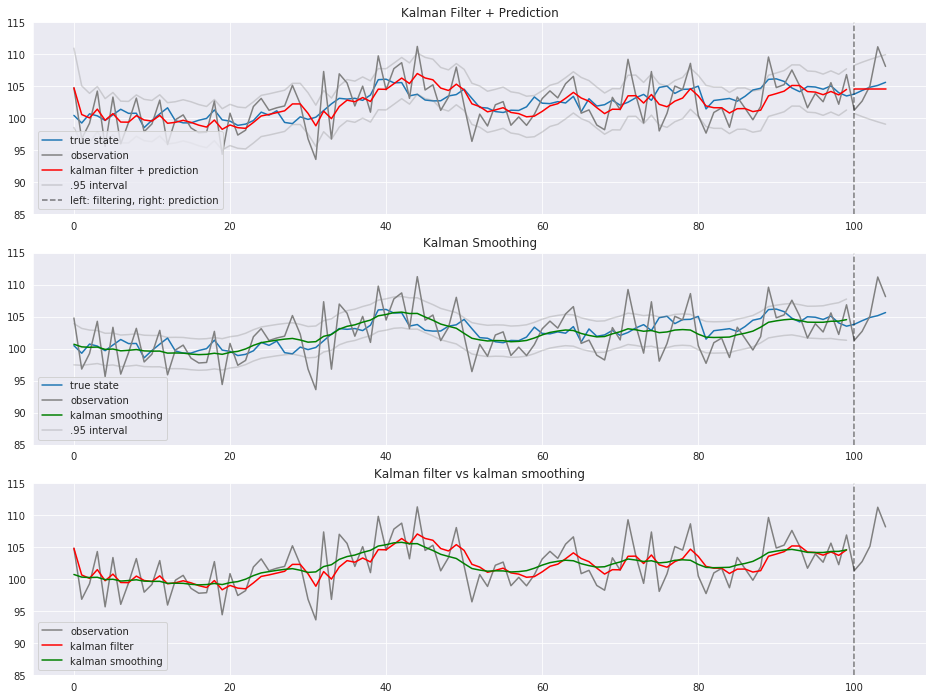
青が真の状態、グレーが観測値、赤がカルマンフィルタ、緑がカルマン平滑化です。 カルマンフィルタ(赤)やカルマン平滑化(緑)と真の状態(青)がそれなりに近しい動き方をしていることがわかります。
観測誤差をある程度取り除いて状態を推定できました。
カルマンフィルタと比べ、カルマン平滑化の方が分散が小さくなっています。
カルマン予測は時点を追うごとに分散が大きくなっています。
過去と現在の情報から状態を推測するカルマンフィルタに比べ、カルマンフィルタの結果を1期先の平滑化分布で補正するカルマン平滑化の方が、よりなだらかです。
いかがでしたでしょうか
まとめ
- カルマンフィルタは観測値$y_{1:t}$から状態$x_t$を求める手法
- 観測誤差のノイズを取り除いて、状態を推定することができる
- pythonで実装してみた
TO DO
もっと複雑なモデルに対する適用