きっかけ
ベータ分布という名前を聞いたことはあるでしょうか。
ベータ分布は、コインの表裏のような2値のいずれかを選ぶときに用いられるベルヌーイ分布や二項分布などの、共役事前分布としてよく使われる確率分布です。正の実数a, bを定義したときμ ∈ (0, 1)となるμの取りうる確率を生成します。
この分布は2つのパラメータによって制御されるのですが、2つの値の取り方によって分布の形がとても大きく変化します。そのため、多くの参考書では様々なパラメータで分布の形がどう変わるのか挿絵を入れています。
今回は対話型の描画が出来るBokehというモジュールを用いて、2つのパラメータを自由に操作しながら分布の動きをリアルタイムに確認できる図を作っていきたいと思います。
(参考)ベータ分布の数式的な理解
ベータ分布とは確率密度関数が
$$
Beta(\mu | a, b) = C_B(a, b) \mu^{a-1} (1 - \mu)^{b-1}
$$
という式になる分布です。
Cは正規化項で
$$
C_B(a, b) = \frac{\Gamma(a + b)}{\Gamma(a) \Gamma(b)}
$$
と定義されます。
Γはガンマ関数といい、
$$
\Gamma(x) = \int t^{x-1} e^{-t}dt
$$
と定義されます。
これは階乗(n!)を一般化したもので、
$$
\Gamma(x+1) = x \Gamma(x)
$$
$$
\Gamma(1) = 1
$$
という性質より、自然数nに対しては
$$
\Gamma(n+1) = n!
$$
が成り立ちます。
Bokehについて
Bokeh公式サイトのQuickstartを真ん中くらいまでやれば基本的な操作はだいたい掴めるかと思います。
ざっくり説明していくと、Bokehは
- Bokeh.models(低レベル、自由度高)
- Bokeh.plotting(高レベル、自由度低)
2つのAPIがあります。基本的には後者のplottingを用います。
どんなときに使えるか
Bokehは描画した後から描画領域などを細かく調整し、調整し終わった図をpngで保存出来ます。
そのため、時系列の折れ線グラフなど、描画範囲やX軸やY軸の広さを細かく調整したいときに重宝します。
また、今回のように変数を調整すると分布がどう変化するかを試すときにも役に立ちます。
インストール
pip install bokeh
描画
bokeh.plottingの基本的な流れは
- データの準備(list, numpy.array, pandas.Series, etc)
- 出力先の指定(output_file("filepath")でhtml出力 or output_notebook()でnotebook埋め込み出力)
- figure()を作成
- renderer(形式的なデータを適切なルールに従って描画するためのシステム)を追加
- 結果をshow()かsave()する
となっています。
output_notebook()を宣言するときは、ノートブックの冒頭で宣言する必要があります。
描画例1
# 折れ線グラフをhtml出力する
from bokeh.plotting import figure, output_file, show
# データの作成
x = [1, 2, 3, 4, 5]
y = [6, 7, 2, 4, 5]
# 出力HTMLファイルパスを指定
output_file("outputs/lines.html")
# タイトルと軸ラベルを指定したfigureを定義
p = figure(title = "simple line example", x_axis_label = "x", y_axis_label = "y")
# プロットに判例と線の暑さを指定したrenderer(今回は折れ線グラフ)を追加
p.line(x, y, legend = "Temp", line_width = 2)
# 結果を描画
show(p)

新しいウィンドウが立ち上がって折れ線グラフが出力されます。
htmlファイルが保存されるので、ローカル環境でいつでも開く事が出来ます。
Jupyter notebookとの連携
output_file(PATH)ではなく、output_notebook()と冒頭に宣言する事で、Jupyter notebookに描画を埋め込む事が出来ます。また、Jupyter上にスライドバーなどを作って描画内容を後からリアルタイムに変更出来ます。
ここにある
"Jupyter Interactors.ipynb", "Numba Image Example.ipynb"
を実行してみるといいでしょう。
上記ファイルをGitHub上で開き、画面右側にある「Raw」ボタンのURLをコピーし、ターミナルで
wget COPIED_URL LOCAL_PATH
と実行すれば、ローカル環境の好きなパスにipynbファイルをダウンロードします。
後は、jupyter notebookを起動し、落としたファイルがあるディレクトリに移動し、クリックすれば実行できます。
描画例2:Jupyterで動く対話型の描画例
# ライブラリの読み込み
from ipywidgets import interact
import numpy as np
from bokeh.io import push_notebook, show, output_notebook
from bokeh.plotting import figure
# 出力先の宣言
output_notebook()
# データの定義
x = np.linspace(0, 2*np.pi, 2000)
y = np.sin(x)
# figure()を宣言
p = figure(title = "simple line example",
plot_height = 300,
plot_width = 600,
y_range = (-5, 5))
# rendererを追加
# ただp.line()とするのではなく、変数rに格納する
r = p.line(x, y, line_width = 3)
# グリグリ動かすボタンを作るには、Interactorを定義する
# 今回は、f, w, A, phiという4変数を動かすことで"r"と名付けたrendererを操作する
def update(f, w=1, A=1, phi=0):
if f == "sin": func = np.sin
elif f == "cos": func = np.cos
elif f == "tan": func = np.tan
r.data_source.data['y'] = A * func(x * w + phi)
push_notebook()
# 描画
show(p, notebook_handle = True) # notebook_handle = Trueにすると、後から描画内容を操作出来る

# interactorの実行
# []はプルダウンリスト、()はスライダー
interact(update, f = ["sin", "cos", "tan"], w = (0, 100), A = (0, 5), phi = (0, 20, 0.1))

こんな感じでウィジェットが出て来ます。
後はfをcosやtanにしたり、スライダーをいじって遊びましょう。
グリグリ動かせるベータ分布の描画
チュートリアルからの抜粋はこれくらいにしておいて、本題に入りましょう。
まず、ベータ分布を作るには確率密度関数を定義します。
Pythonで数値計算といえばnumpyが有名ですが、今回はsympyを使います。
numpyは数値配列(離散的なデータ)を扱うのに対し、sympyは数式を数式のまま扱ってくれるからです。
例えば、numpyは無理数に対して近似的な計算をしてしまいますが、sympyは無理数を無理数のままで計算するので、理論上誤差が発生しません。
詳細はここを参照してみてください。
### 必要なモジュールの読み込み、設定
import numpy as np
from sympy import *
from ipywidgets import interact
from bokeh.io import push_notebook, show, output_notebook
from bokeh.plotting import figure, output_file
output_notebook() # 描画をjupyter notebookに出力
### 描画
## 1.データの定義
data_x_array = np.arange(0, 1, 0.01)
data_mu_array = np.arange(0, 1, 0.01)
def my_beta(data_a, data_b, data_mu):
'''
ベータ分布の確率密度関数
a, bを設定した上で任意のmuを入れると、muがその値である確率を返す
data_a: a > 0
data_b: b > 0
data_mu: 0 <= mu <= 1
'''
# sympyでは、変数に使うアルファベットをあらかじめ定義する
# ここで使用したアルファベットを他の変数として使ってはならない
a, b, t, x, mu = symbols('a b t x mu')
# 関数の定義
Gamma = Integral(t**(x - 1) * exp(-t), (t, 0, oo)) # ガンマ関数、この段階では積分を定義するだけで計算は行わない
C = Gamma.subs(x, a + b) / (Gamma.subs(x, a) * Gamma.subs(x, b)) # ベータ分布の正規化項
Beta = C * mu**(a - 1) * (1 - mu)**(b - 1) # ベータ分布の確率密度関数
# a, bが与えられたときのmuの確率を計算
prob = Beta.subs([(a, data_a), (b, data_b), (mu, data_mu)]).doit() # doit()は積分を計算するコマンド
return np.float(prob)
data_prob_array = np.array([my_beta(1, 1, data_mu) for data_mu in data_mu_array]) # デフォルトではa=1, b=1の分布を描画する
# beta(a, b, mu)はsympy.core.numbers.NUMBERを返すので、floatに変換する必要がある
## 2.出力先の指定
# output_file("beta.html") # html保存をしたいときは#を外す
## 3.figureを宣言
p = figure(title = "Beta distribution",
plot_height = 300,
plot_width = 600,
y_range = (0, 8))
## 4.rendererを追加
r = p.line(data_x_array, data_prob_array, line_width = 3)
## 5.interactorを定義
def update(data_a=1, data_b=1):
r.data_source.data['y'] = np.array([my_beta(data_a, data_b, data_mu) for data_mu in data_mu_array])
push_notebook()
## 6.描画
show(p, notebook_handle=True) # notebook_handleをTrueにすると後から図を制御出来る
## 7.interactorの実行
interact(update, data_a = (0, 20, 0.5), data_b = (0, 20, 0.5))

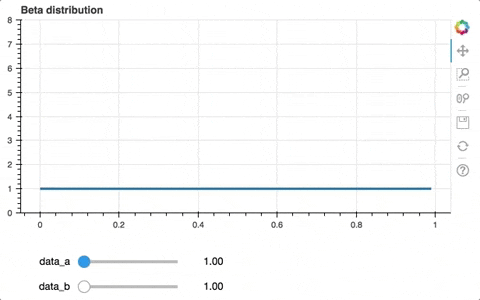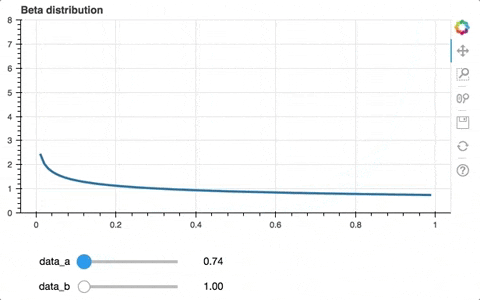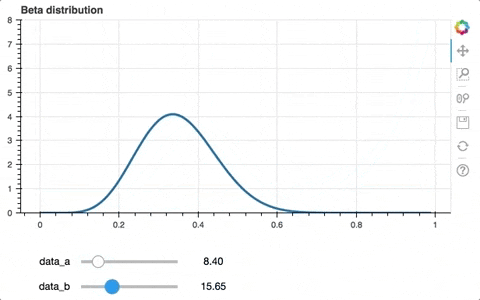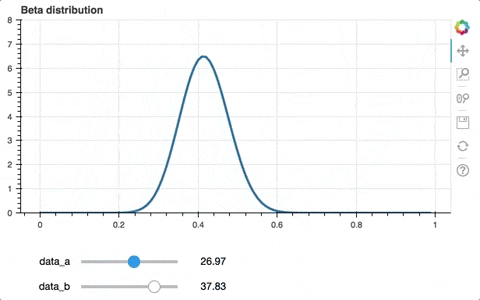
描画出来ました。
上図より、ベータ分布はa = b = 1のとき一様分布になっていることがわかります。
scipyを使って遅延を無くす
上の図は一見問題なく描画出来ていますが、1つ問題があります。それは、スライダーを動かした時に図が動くまでとても時間がかかる事です。確率密度関数を自作したため、計算が遅くなっているのです。
そこで、scipy.stats.beta.pdf()を用いてinteractorを改良します。
# モジュールの読みこみ
from scipy.stats import beta
# update関数の改良
def update_scipy(data_a = 1, data_b = 1):
r.data_source.data['y'] = np.array([beta.pdf(data_mu, data_a, data_b) for data_mu in data_mu_array])
push_notebook()
# 再び描画
show(p, notebook_handle=True)
interact(update_scipy, data_a = (0.01, 50, 0.01), data_b = (0.01, 50, 0.01))
かっこいい!
aを大きくすればするほど右側(μ=1側)の確率が上がったり、aやbの値が大きい方が尖度(尖り具合)が大きいことがわかります。
スライダーのメモリを0~1と1以上で変えたほうが良さそうですが、それはまたの機会に。
まとめ
- ベータ分布はベルヌーイ分布や二項分布の共役事前分布
- ベータ分布はa,b2つのパラメータから任意のμを生成する確率を求める分布
- Bokehは対話型の描画が出来るモジュール
- Jupyterに図を埋め込んだりウィジェットで図をグリグリ動かせるが、場合によっては遅延する
終わりに
客先などにこういうグリグリ動く図を見せるとわかりやすく「すごい」と思わせられるので、覚えておいて損は無いです。
公式のギャラリーにたくさんの描画例が載っているので、これから色々な図を試していこうと思います。