C#で実装するトップダウン型自動微分

#自動微分とは

　自動微分(Automatic Differentiation, AD)とは、その名の通り自動で微分する技術のことです。プログラム上での微分手法には、$\frac{f(x+h)-f(x)}{h}$みたいな計算をして求める数値微分や、数式処理によって偏導関数を求める数式微分などがありますが、自動微分ではどちらとも違う手法で微分値を求めることができます。

　自動微分にはボトムアップ型の手法とトップダウン型の手法があり、以下のページではボトムアップ型の実装を紹介しています。

• 二重数で自動微分する
• ボトムアップ型自動微分の実験

　今ブームのニューラルネットワークで用いられている誤差逆伝播法はトップダウン型自動微分の一種ということなので、ここではトップダウン型の実装に挑戦してみようと思います。言語はC#。

#考え方

　自動微分では、合成関数の微分の考え方を利用します。

f(g_1(x),g_2(x),\cdots) \Rightarrow
\frac{\partial f}{\partial x} = \frac{\partial f}{\partial g_1}\frac{dg_1}{dx} + \frac{\partial f}{\partial g_2}\frac{dg_2}{dx} + \cdots

　自動微分では、対象となる関数を対象となる関数を単純な関数に分解して計算グラフで考えます。たとえば、$y=a\exp(x)\times(\exp(x)+b)$から$\frac{\partial y}{\partial x}$を求めることを考えます。$y$を初等関数や四則演算に分解して、各演算に変数名を振ると、

\begin{align}
c&=\exp(x)\\
d&=ac\\
e&=c+b\\
f&=d+e\\
y&=f
\end{align}

となり、以下のような計算グラフで表せます。各ノードが中間変数、各エッジが演算の入出力関係を示しています。

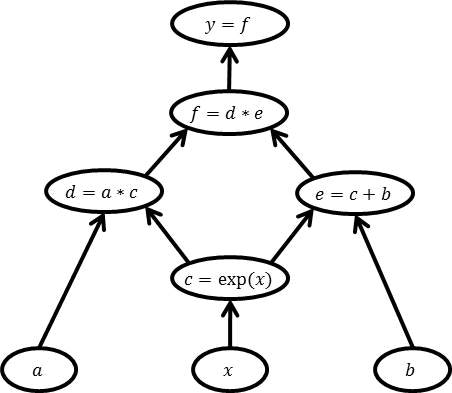
　各演算は単純なものなので、微分値を計算することができます。この微分値と各エッジを対応付けて考えます。

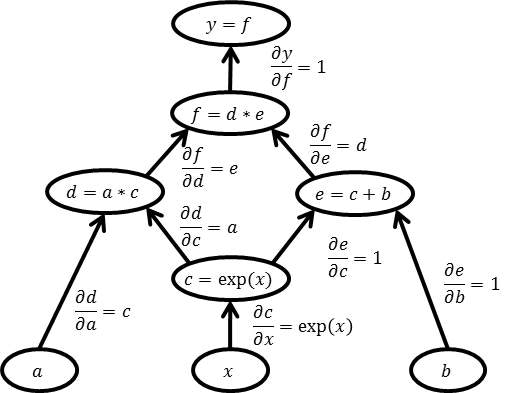
　グラフを見てわかるように$c$以外は直接$x$の関数ではないので、合成関数の考え方から、$\frac{\partial y}{\partial x}=\frac{\partial y}{\partial c}\frac{\partial c}{\partial x}$となります。また同様に、$\frac{\partial y}{\partial c}=\frac{\partial x}{\partial d}\frac{\partial d}{\partial c}+\frac{\partial x}{\partial e}\frac{\partial e}{\partial c}$となります。ですので、上から順に

\begin{align}
\frac{\partial y}{\partial f} &= 1\\
\frac{\partial y}{\partial d} &= \frac{\partial y}{\partial f}\frac{\partial f}{\partial d} = 1 \cdot e = e\\
\frac{\partial y}{\partial e} &= \frac{\partial y}{\partial f}\frac{\partial f}{\partial e} = 1 \cdot d = d\\
\frac{\partial y}{\partial a} &= \frac{\partial y}{\partial d}\frac{\partial d}{\partial a} = ce\\
\frac{\partial y}{\partial c} &= \frac{\partial y}{\partial d}\frac{\partial d}{\partial c} + \frac{\partial y}{\partial e}\frac{\partial e}{\partial c}= ae+d \cdot 1=ae+d\\
\frac{\partial y}{\partial b} &= \frac{\partial y}{\partial e}\frac{\partial e}{\partial b} = d \cdot 1 = d\\
\frac{\partial y}{\partial x} &= \frac{\partial y}{\partial c}\frac{\partial c}{\partial x} = (ae+d)\exp(x)
\end{align}

と計算することで$\frac{\partial y}{\partial x}$を求めることができます。
　この考えを、プログラムで実装していきたいと思います。

#実装

##計算グラフの構築

　まず、計算グラフを構築できるような自動微分型クラスを考えます。一つのインスタンスが一つの演算や変数を表すとして、演算の出力値、入力値、入力変数による偏導関数値をメンバとして持つように実装するとこんな感じでしょうか。

namespace AutoDiff
{
    /// <summary>
    /// 自動微分を実現するクラス
    /// 一つのインスタンスが一つの演算や変数を示す
    /// </summary>
    public class AD
    {
        /// <summary>
        /// 演算の出力値
        /// </summary>
        private double Output;
        /// <summary>
        /// 演算の入力
        /// </summary>
        private AD[] Inputs;
        /// <summary>
        /// 入力変数による偏導関数値
        /// </summary>
        private double[] Differentials;

        /// <summary>
        /// 変数を表すコンストラクタ
        /// </summary>
        /// <param name="v">変数値</param>
        public AD(double v)
        {
            Output = v;
            Inputs = null;
            Differentials = null;
        }
        /// <summary>
        /// 演算を表すコンストラクタ
        /// </summary>
        /// <param name="v">演算の結果値</param>
        /// <param name="InputNum">入力の数</param>
        private AD(double v, int InputNum)
        {
            Output = v;
            Inputs = new AD[InputNum];
            Differentials = new double[InputNum];
        }
        /// <summary>
        /// 暗黙の型変換
        /// </summary>
        public static implicit operator AD(double v)
        {
            return new AD(v);
        }
    }
}

　演算を表すコンストラクタは外から直接呼ぶことはないのでprivateにしてあります。四則演算はオペレータオーバーロードで、初等関数はstaticなメンバ関数として実装します。

public class AD
{
    :
    /// <summary>
    /// 入力変数と対応する偏微分値を追加する
    /// </summary>
    private void AddInput(int index, AD input, double diff)
    {
        this.Inputs[index] = input;
        this.Differentials[index] = diff;
    }
    /// <summary>
　  /// +演算子のオーバーロード
　  /// </summary>
    public static AD operator +(AD x, AD y)
    {
        var z = new AD(x.Output + y.Output, 2);
        z.AddInput(0, x, 1);
        z.AddInput(1, y, 1);
        return z;
    }
    /// <summary>
    /// *演算子のオーバーロード
    /// </summary>
    public static AD operator *(AD x, AD y)
    {
        var z = new AD(x.Output * y.Output, 2);
        z.AddInput(0, x, y.Output);
        z.AddInput(1, y, x.Output);
        return z;
    }

    /// <summary>
    /// Exp関数
    /// </summary>
    public static AD Exp(AD x)
    {
        var z = new AD(Math.Exp(x.Output), 1);
        z.AddInput(0, x, z.Output);
        return z;
    }

    // 他の関数はいったん略
}

　AddInputは、指定したインデックスのInputsとDifferentialsに入力変数と対応する偏微分値を格納する関数です。$\frac{\partial}{\partial x}(x+y)=1,\frac{\partial}{\partial y}(x+y)=1$なので、+演算子のオーバーロードの中でxを格納したInputsに対応するDifferentialsに1を入れ、yに対応するDifferentialsにも1を入れています。同様に、$\frac{\partial}{\partial x}(x\cdot y)=y,\frac{\partial}{\partial y}(x\cdot y)=x$なので、*演算子のオーバーロードの中で、x,yに対応するDifferentialsにそれぞれy,xの出力値を入れています。またExp関数に関しては、$\frac{\partial}{\partial x}\exp(x)=\exp(x)$で、出力値と等しくなるので、Differentialsに自身の出力値を入れています。
　このように実装することで、自然に計算グラフを構築できるクラスを実現できます。上記計算グラフは、たとえば

var x = new AD(1);
var a = 2;
var b = 3;

var c = AD.Exp(x);
var d = a * c;
var e = c + b;
var f = d * e;
var y = f;

等とすることによって構築できます。

##微分機能の実装

微分を行うメンバ関数GetDifferentialを実装します。この関数は、上記AD型変数yに対してy.GetDifferential()とすると、$\frac{\partial y}{\partial a},\frac{\partial y}{\partial b},\ldots,\frac{\partial y}{\partial x}$を取得できるような関数です。

以下のような考え方でこの関数を実装します。

• yに対する偏微分値を表すメンバ変数difを持たせる。
• difを0で初期化する。
  • 微分計算を行う際、計算グラフをたどって、各ノードのdifを初期化する。
• yのdifを1にする。
  • $\frac{\partial y}{\partial y}=1$は自明。
• 偏微分値の計算が完了した変数の入力に、入力に対応する偏微分値×自身の偏微分値を足しこんでいく。
  • $y(f_1(x),f_2(x),\ldots)$のとき、$\frac{\partial y}{\partial x} \gets \frac{\partial y}{\partial x} + \frac{\partial y}{\partial f_i}\frac{\partial f_i}{\partial x}$という操作を$f_1,f_2,\ldots$に対して行うことで
    $\frac{\partial y}{\partial x}=\frac{\partial y}{\partial f_1}\frac{\partial f_1}{\partial x} + \frac{\partial y}{\partial f_2}\frac{\partial f_2}{\partial x} + \cdots$を計算できる。
• 偏微分値の計算完了を判定するために、他の演算の入力として使われている回数を表すメンバ変数UsedNum、偏微分値の足しこみが行われた回数を表すメンバ変数CalculatedNumを持たせる。
  • difの初期化の際にUsedNumをインクリメントしていき、偏微分値の足しこみの際にCalculatedNumをインクリメントする。
  • UsedNumとCalculatedが等しくなったら計算完了とみなすことができる。

この考えでGetDifferentialを実装すると、

public class AD
{
    :
    /// <summary>
    /// 偏微分値
    /// </summary>
    private double dif = 0;
    
    /// <summary>
    /// この変数を入力として使っている演算の数
    /// </summary>
    private int UsedNum;
    /// <summary>
    /// 偏微分値の足しこみ回数
    /// </summary>
    private int CalculatedNum;

    /// <summary>
    /// 計算待機リスト
    /// </summary>
    private static Queue<AD> CalcList = new Queue<AD>();

    /// <summary>
    /// 準備中フラグ
    /// </summary>
    private bool InPreparation = false;

    /// <summary>
    /// 微分計算
    /// </summary>
    public void GetDifferential()
    {
        // 待機リストが空になるまでループして全ノードで準備
        CalcList.Enqueue(this);
        while (CalcList.Count > 0)
        {
            CalcList.Dequeue().prepare();
        }

        // 目的関数自身による微分値は1になる
        this.dif = 1.0;

        // 待機リストが空になるまでループして全ノードで計算
        CalcList.Enqueue(this);
        while (CalcList.Count > 0)
        {
            CalcList.Dequeue().calculate();
        }
    }
    /// <summary>
    /// 偏微分計算の準備
    /// </summary>
    private void prepare()
    {
        // すでに計算準備を行っているなら何もしない
        if (this.InPreparation) return;
        this.InPreparation = true;

        this.dif = 0;
        this.CalculatedNum = 0;

        if (Inputs == null) return;
        for (int i = 0; i < Inputs.Length; i++)
        {
            var src = Inputs[i];
            src.UsedNum++;
            if (!src.InPreparation)
                CalcList.Enqueue(src);
        }
    }
    /// <summary>
    /// 偏微分値計算
    /// </summary>
    protected void calculate()
    {
        // すでに偏微分値計算を行っているなら何もしない
        if (!this.InPreparation) return;
        this.InPreparation = false;

        if (Inputs== null) return;
        for (int i = 0; i < Inputs.Length; i++)
        {
            var src = Inputs[i];
            src.dif += this.dif * Differentials[i];
            src.CalculatedNum++;
            // 計算回数が演算ソースとして使われている回数に達した（＝微分値導出完了）なら待機リストに加える
            if (src.CalculatedNum >= src.UsedNum)
            {
                src.UsedNum = 0;
                CalcList.Enqueue(src);
            }
        }
    }

    /// <summary>
    /// 変数値、演算の結果値
    /// </summary>
    public double Val { get { return Output; } }
    /// <summary>
    /// 偏微分値
    /// </summary>
    public double Dif { get { return dif; } }
}

　ValとDifは変数値や偏微分値を取得するためのプロパティです。y.GetDifferential()とやると、x.Difが$\frac{\partial y}{\partial x}$を表す値になります。
　基本的には上で書いた考え方の通りに実装していますが、いくつか実装上の都合で変わっている部分を説明します。
　計算グラフの頂点からグラフをたどる場合、グラフの形によっては同じノードを複数回たどることになります。重複してノードをたどってしまうと、UsedNumの数がずれたり、偏微分値の足しこみが重複して正しい結果を計算できなくなります。InPreparationというメンバ変数を用意して、ノードの状態を管理することで、重複計算を回避しています。
　また、CalcListというキューをstaticで用意して、計算待機リストとして使っています。prepare関数やcalculate関数の中で入力ノードをCalcListに追加して、GetDifferential関数の中でwhileを回してCalcListに追加したノードでprepareやcalculateすることで、計算グラフをたどりながら計算することを実現しています。関数の再帰等の手法でも実現できますが、複雑な演算を微分する場合、再帰だとスタックオーバーフローする可能性があるのでこのような手法を使いました。
　for文のところはLINQとか使った方がかっこいいかなとも思いましたが、実行速度を優先してこんな風になりました。

##その他の関数

　簡単のため和積とExp関数しか実装しませんでしたので、他の四則演算やよく使う関数も実装します。

public class AD
{
    :
    /// <summary>
    /// +単項演算子のオーバーロード
    /// </summary>
    public static AD operator +(AD x)
    {
        var z = new AD(x.Output, 1);
        z.AddInput(0, x, 1);
        return z;
    }
    /// <summary>
    /// -単項演算子のオーバーロード
    /// </summary>
    public static AD operator -(AD x)
    {
        var z = new AD(-x.Output, 1);
        z.AddInput(0, x, -1);
        return z;
    }
    /// <summary>
    /// -演算子のオーバーロード
    /// </summary>
    public static AD operator -(AD x, AD y)
    {
        var z = new AD(x.Output - y.Output, 2);
        z.AddInput(0, x, 1);
        z.AddInput(1, y, -1);
        return z;
    }
    /// <summary>
    /// /演算子のオーバーロード
    /// </summary>
    public static AD operator /(AD x, AD y)
    {
        var z = new AD(x.Output / y.Output, 2);
        z.AddInput(0, x, 1 / y.Output);
        z.AddInput(1, y, -x.Output / (y.Output * y.Output));
        return z;
    }

    /// <summary>
    /// Sqrt関数
    /// </summary>
    public static AD Sqrt(AD x)
    {
        var z = new AD(Math.Sqrt(x.Output), 1);
        z.AddInput(0, x, 0.5 / z.Output);
        return z;
    }
    /// <summary>
    /// Log関数
    /// </summary>
    public static AD Log(AD x)
    {
        const double delta = 1e-13;
        var z = new AD(Math.Log(x.Output + delta), 1);
        z.AddInput(0, x, 1 / (x.Output + delta));
        return z;
    }
    /// <summary>
    /// Log関数
    /// </summary>
    public static AD Log(AD x, double a)
    {
        const double delta = 1e-13;
        var z = new AD(Math.Log(x.Output + delta, a), 1);
        z.AddInput(0, x, 1 / ((x.Output + delta) * Math.Log(a)));
        return z;
    }
    /// <summary>
    /// Sin関数
    /// </summary>
    public static AD Sin(AD x)
    {
        var z = new AD(Math.Sin(x.Output), 1);
        z.AddInput(0, x, Math.Cos(x.Output));
        return z;
    }
    /// <summary>
    /// Cos関数
    /// </summary>
    public static AD Cos(AD x)
    {
        var z = new AD(Math.Cos(x.Output), 1);
        z.AddInput(0, x, -Math.Sin(x.Output));
        return z;
    }
    /// <summary>
    /// Tan関数
    /// </summary>
    public static AD Tan(AD x)
    {
        var z = new AD(Math.Tan(x.Output), 1);
        double cos = Math.Cos(x.Output);
        z.AddInput(0, x, 1 / (cos * cos));
        return z;
    }
    /// <summary>
    /// Tanh関数
    /// </summary>
    public static AD Tanh(AD x)
    {
        var z = new AD(Math.Tanh(x.Output), 1);
        z.AddInput(0, x, 1 - z.Output * z.Output);
        return z;
    }
    /// <summary>
    /// 絶対値関数
    /// </summary>
    public static AD Abs(AD x)
    {
        var z = new AD(Math.Abs(x.Output), 1);
        z.AddInput(0, x, x.Output < 0 ? -1 : 1);
        return z;
    }
    /// <summary>
    /// Max関数
    /// </summary>
    public static AD Max(AD x, AD y)
    {
        return x.Output > y.Output ? +x : +y;
    }
    /// <summary>
    /// Min関数
    /// </summary>
    public static AD Min(AD x, AD y)
    {
        return x.Output < y.Output ? +x : +y;
    }
    /// <summary>
    /// Sigmoid関数
    /// </summary>
    public static AD Sigmoid(AD x)
    {
        var z = new AD(1 / (1 + Math.Exp(-x.Output)), 1);
        z.AddInput(0, x, (1 - z.Output) * z.Output);
        return z;
    }
    /// <summary>
    /// Rectified Linear Unit
    /// </summary>
    /// <param name="x"></param>
    /// <returns></returns>
    public static AD ReLU(AD x)
    {
        var z = new AD(Math.Max(0, x.Output), 1);
        z.AddInput(0, x, x.Output > 0 ? 1 : 0);
        return z;
    }
    /// <summary>
    /// 累乗関数 x^y
    /// </summary>
    public static AD Pow(AD x, AD y)
    {
        var z = new AD(Math.Pow(x.Output, y.Output), 2);
        z.AddInput(0, x, y.Output * Math.Pow(x.Output, y.Output - 1));
        z.AddInput(1, y, z.Output * Math.Log(x.Output));
        return z;
    }
    /// <summary>
    /// 平均関数
    /// </summary>
    public static AD Average(AD[] X)
    {
        var z = new AD(0, X.Length);
        for (int i = 0; i < X.Length; i++)
        {
            z.Output += X[i].Output;
            z.AddInput(i, X[i], 1.0 / X.Length);
        }
        z.Output /= X.Length;
        return z;
    }
    /// <summary>
    /// 合計関数
    /// </summary>
    public static AD Sum(AD[] X)
    {
        var z = new AD(0, X.Length);
        for (int i = 0; i < X.Length; i++)
        {
            z.Output += X[i].Output;
            z.AddInput(i, X[i], 1);
        }
        return z;
    }
    /// <summary>
    /// 内積関数
    /// </summary>
    public static AD InnerProd(AD[] X, AD[] Y)
    {
        var N = Math.Min(X.Length, Y.Length);
        var z = new AD(0, 2 * N);
        for (int i = 0; i < N; i++)
        {
            z.Output += X[i].Output * Y[i].Output;
            z.AddInput(i, X[i], Y[i].Output);
            z.AddInput(i + N, Y[i], X[i].Output);
        }
        return z;
    }
}

　あまり使わないような関数もついでに実装してみました。AbsやMax等の関数も（無理矢理）微分できるのが自動微分の特徴です。SigmoidやReLUはニューラルネットワーク等で頻繁に使用される関数なので実装してみました。また、平均や合計や内積関数を見てわかるように、入力変数が3つ以上になる関数も実装可能です。

#試してみる

　実際に、試してみました。

AD x;
AD y;

x = 1;
var a = 2;
var b = 3;

// y = (a * exp(x)) * (exp(x) + b)
var c = AD.Exp(x);
var d = a * c;
var e = c + b;
var f=d * e;
y = f;            
y.GetDifferential();
// yとdy/dxを出力
Console.WriteLine(y.Val + "\t" + x.Dif);

// 中間変数に分けなくてもいける
y = (a * AD.Exp(x)) * (AD.Exp(x) + b);
y.GetDifferential();
// yとdy/dxを出力
Console.WriteLine(y.Val + "\t" + x.Dif);

// y = 5x^2 をループで書く
x = 3;
y = 0;
for (int i = 0; i < 5; i++) y += x * x;
y.GetDifferential();
// yとdy/dxを出力
Console.WriteLine(y.Val + "\t" + x.Dif);

// y = (x - 5)^2 の極小値を最急降下法で求める
x = 20; // 適当な初期値
while (true)
{
    y = (x - 5) * (x - 5);
    y.GetDifferential();
    if (x.Dif * x.Dif < 1e-20) break; // 終了判定
    x = x.Val- 0.1 * x.Dif; // xの更新
}
// yの極小値とその時のx
Console.WriteLine(y.Val + "\t" + x.Val);

実行結果

31.0878031686156        45.8659153664769
31.0878031686156        45.8659153664769
45      30
1.93908103743843E-21    5.00000000004404

　$x=1,a=2,b=3$のとき、

\begin{align}
y=a\exp(x)(\exp(x)+b)&=31.0878\cdots\\
\frac{\partial y}{\partial x}=2a\exp(2x)+ab\exp(x)&=45.8659\cdots
\end{align}

となるので、微分計算できていることがわかります。ループを使うような計算や、最急降下法等への応用もできているようです。

　最急降下法で注意が必要なのは、xの更新で x -= 0.1 * x.Dif とせずに x = x.Val - 0.1 * x.Dif としている点です。右辺でdouble型にして代入の際に暗黙の型変換で自動微分型に戻しています。一時的にdouble型にすることで、自動微分型の計算グラフを断ち切っています。この程度の計算なら対して問題にはなりませんが、この書き方をしないと、更新前のxが計算グラフに延々と連なってしまいメモリや実行速度の上で不利になります。

　次はADクラスを使ってニューラルネットっぽいものを作ってみたいと思います。

#参考
　実装にあたって、以下のページを参考にしました。

• 自動微分で遊ぼう