強化学習輪読 #11

概要

Chapter6 TD法のちょうど半分 (8.5p/17p)
TD法の概念と性質について．
ポリシーが定められたときの状態価値の推定
数学的なところが少ないので早く終わってしまうかもしれません...

目次

• 6.1 TD prediction
• 6.2 Advantages of TD Prediction Methods
• 6.3 Optimality of TD(0)

Chapter 6 Temporal-Difference Learning

TD法は現在の強化学習の最も中心的なアイディアである．
TD法は，

• Dynamic Programming (DP)　
• Monte Carlo (MC)

を組み合わせたような手法であり，

• エピソードを最後まで行わずにステップごとに価値関数を推定できる
• 環境モデルの動的な情報を知らなくとも価値関数が推定できる

というように両者のいいとこ取りをした方法である．一重にTD法と言っても様々な手法が存在するため，Chapter6ではその基本的なアイディアを説明し，発展的な手法を後のChapterで説明する．
特に，Chapter7ではn-step アルゴリズムやChapter12ではTD(λ)という重要なアルゴリズムを扱う．

この章でも，まずはポリシーπが決められたときの状態(行動)価値を推定(prediciton)する方法を示し，その後最適なポリシーを決定する(control)方法について説明する．(ただし今回はpredictionまで)

6.1 TD Prediction

TD(0)

まずは特定のポリシーπをとるときの状態(行動)価値の推定を行う．最も単純なevery visit MC法では，$G_t$をt期以降の(経験に基づく)リターン，$\alpha$をステップサイズの定数として，

$V(S_t) \gets V(S_t) + \alpha[G_t - V(S_t)]$

という更新を行う．この方法を(constant) α-MC法と呼ぶ．これは経験によって得られたt期以降の報酬の和と古い推定値の差を誤差として考え，その誤差の方向に少し修正するという作業をエピソードごとに繰り返していると言える．しかし，これは各エピソードまで更新を待つ必要がある．

TD法の発想はこのα MC法をタイムステップごとに更新するように変更したものだと見れる．例えば最もシンプルなTD法は，

$V(S_t) \gets V(S_t) + \alpha[R_{t+1} + \gamma V(S_{t+1}) - V(S_t)]$

という更新タイムステップごとに行う方法として表される．これは$S_t$から$S_{t+1}$に遷移してすぐに$G_t$の推定値$R_t + \gamma V(S_{t+1})$を用いて更新を行う方法である(γは割引率)．この方法をTD(0)もしくは one-step TDと呼ぶ(あとで説明するTD(λ)やn-step TDの特殊な形と見れるため)．このアルゴリズムの疑似コードは以下のように表せる．

ここで，DPの場合と同様に，既存の推定値を用いて異なる推定値の更新を行うこのような方法をbootstrappingと呼ぶ．

(p90) they update estimates on the basis of other estimates. We call this general idea bootstrapping.

また，

\begin{align}
v_{\pi}(s)&=\mathbb{E}_{\pi}[G_t\ | \ S_t = s] \\
&=\mathbb{E}_{\pi}[R_{t+1} +\gamma G_{t+1} \ |\ S_t = s]\\
&=\mathbb{E}_{\pi}[R_{t+1} +\gamma v_{\pi}(S_{t+1})\ | \ S_t = s]
\end{align}

であるが，大雑把に言えばMCは一行目の式，TDは3行目の式をターゲットとしていると言える．ただし，TDでは更新時に正確な$v_{\pi}(S_{t+1})$を知らないため，これを暫定解$V(S_{t+1})$で代用する．

TDのバックアップダイアグラム

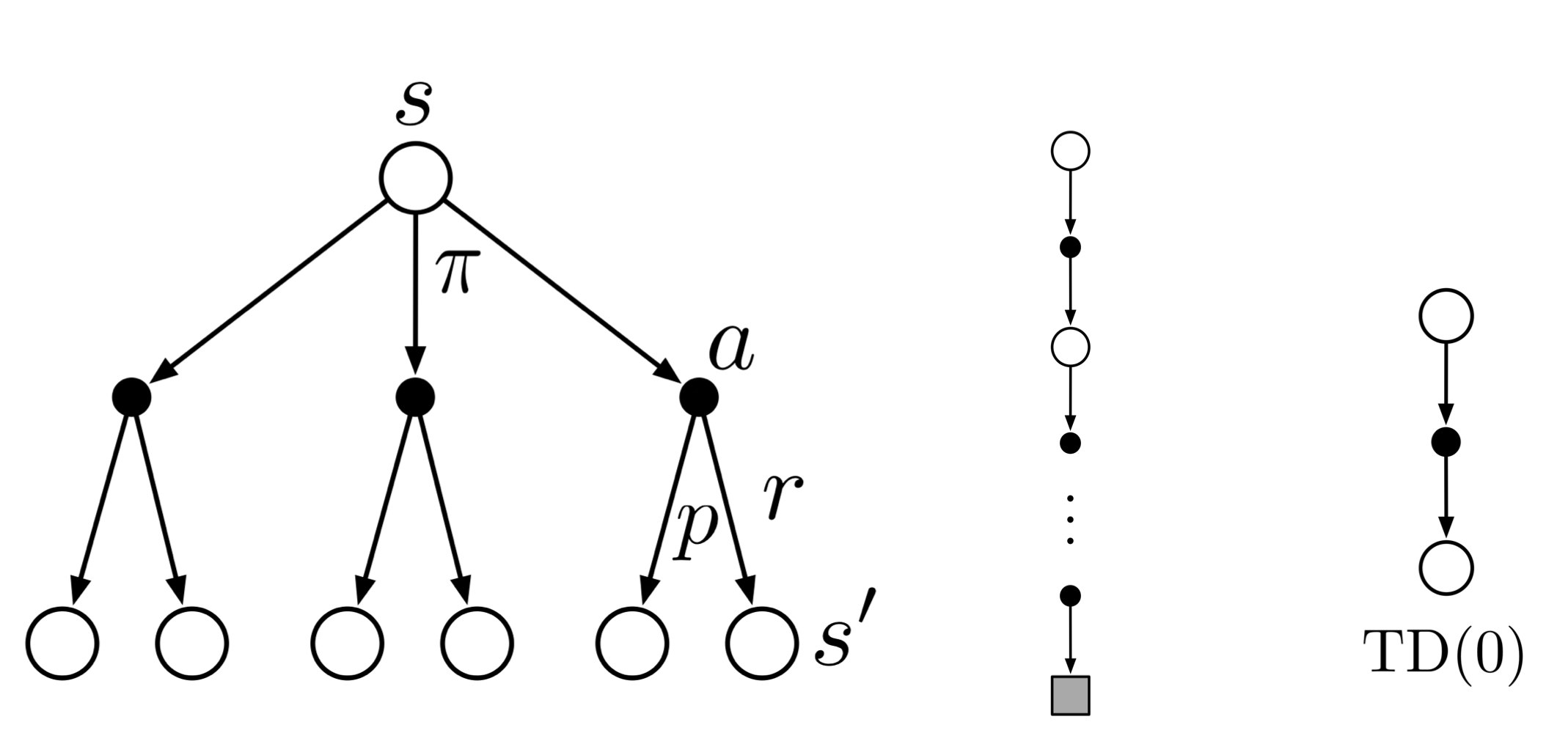
DP，MCと同様にTDでのバックアップダイアグラムは下のように表される．

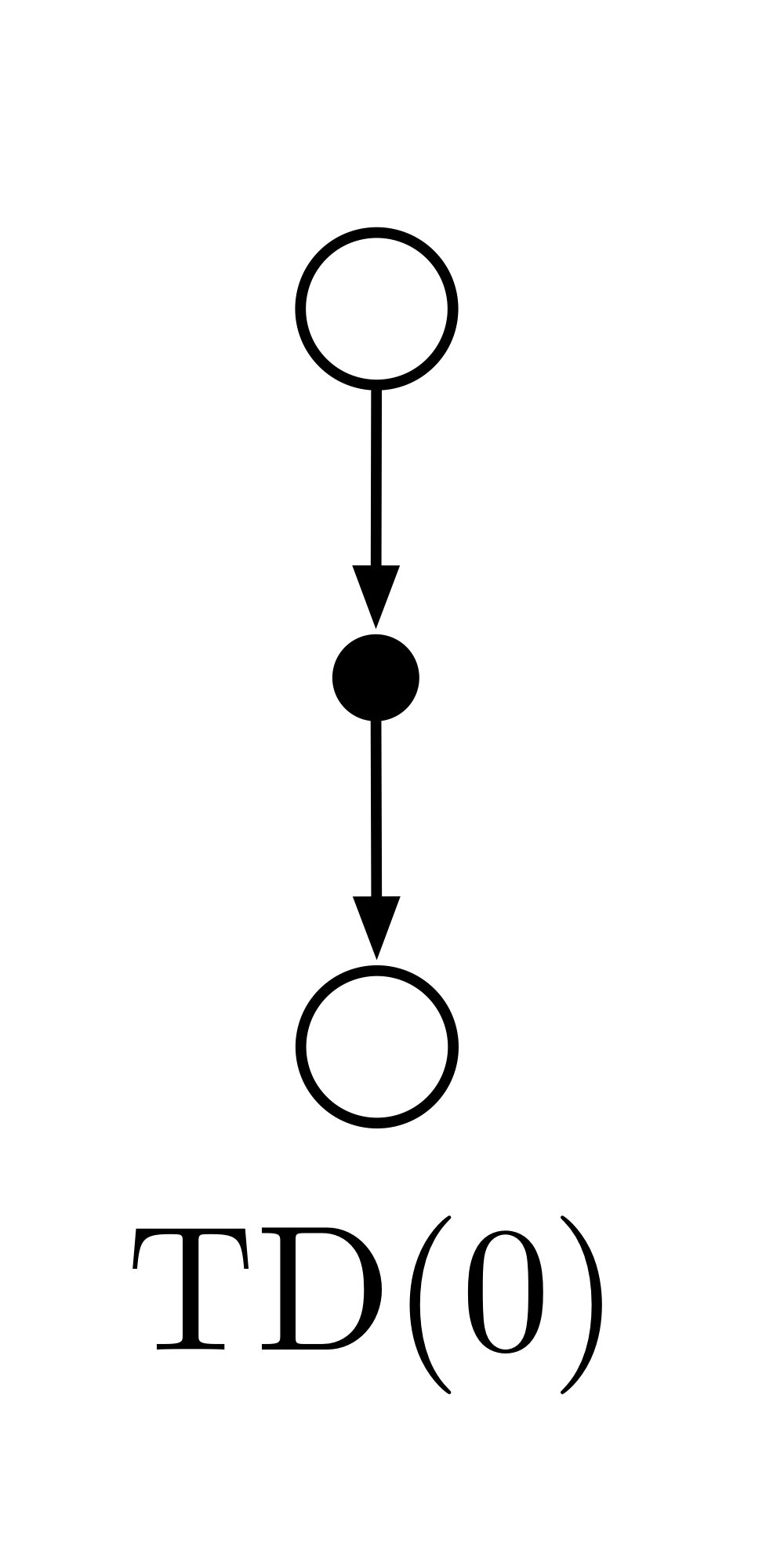
一つ後の状態についてエピソードの終端を待たずに即座に推定値を更新することを表している．

比較(左：MDP/DP, 中：MC，右：TD)

TD error

TD(0)の[]内は$S_t$の暫定推定値とより良い推定値との間の誤差である．この誤差をTD errorと呼ぶ．つまり，TD errorは，

\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t)

と表され，この誤差を減らす方向にステップサイズ$\alpha$を掛けた分修正する.このTD errorは強化学習の多くの場面で現れる．この$V$が終端状態まで変わらないとすると，MC法の更新(3.9)式が，

\begin{aligned} G_{t}-V\left(S_{t}\right) &=R_{t+1}+\gamma G_{t+1}-V\left(S_{t}\right)+\gamma V\left(S_{t+1}\right)-\gamma V\left(S_{t+1}\right) \\ &=\delta_{t}+\gamma\left(G_{t+1}-V\left(S_{t+1}\right)\right) \\ &=\delta_{t}+\gamma \delta_{t+1}+\gamma^{2}\left(G_{t+2}-V\left(S_{t+2}\right)\right) \\ &=\delta_{t}+\gamma \delta_{t+1}+\gamma^{2} \delta_{t+2}+\cdots+\gamma^{T-t-1} \delta_{T-1}+\gamma^{T-t}\left(G_{T}-V\left(S_{T}\right)\right) \\ &=\delta_{t}+\gamma \delta_{t+1}+\gamma^{2} \delta_{t+2}+\cdots+\gamma^{T-t-1} \delta_{T-1}+\gamma^{T-t}(0-0) \\ &=\sum_{k=t}^{T-1} \gamma^{k-t} \delta_{k} \end{aligned}

というようにTD errorの(割引率付きの)和として表される．MCやTDは$V$が正確でないまま更新を行うが，ステップサイズが十分に小さければ近似性は保たれる．この性質がtemporal-difference learningの理論の重要な役割を果たす．

Example 6.1 家への帰宅

状況設定

• 仕事から車で家に帰るとき、家に帰るまでの時間を予測しようとする。

エピソード例

• 18時ちょうどにオフィスを出る．
• 車に着くと18時5分になり，雨が降り始めていることに気づく．雨が降っていると交通の便が悪くなることが多いので，そこから35分，合計40分かかると再計算する．
• 15分後，高速道路の部分を通過．下道に出た時点で想定より5分短縮でき総移動時間を35分に短縮することができた．
• しかし下道でトラックの後ろに入ってしまい，追い抜けずに18時40分までトラックの後を追いかけることになった，
• トラックが前からいなくなって3分後に家に着く．

問題設定

• 報酬：経過時間(× -1)
• 状態価値：期待される移動時間

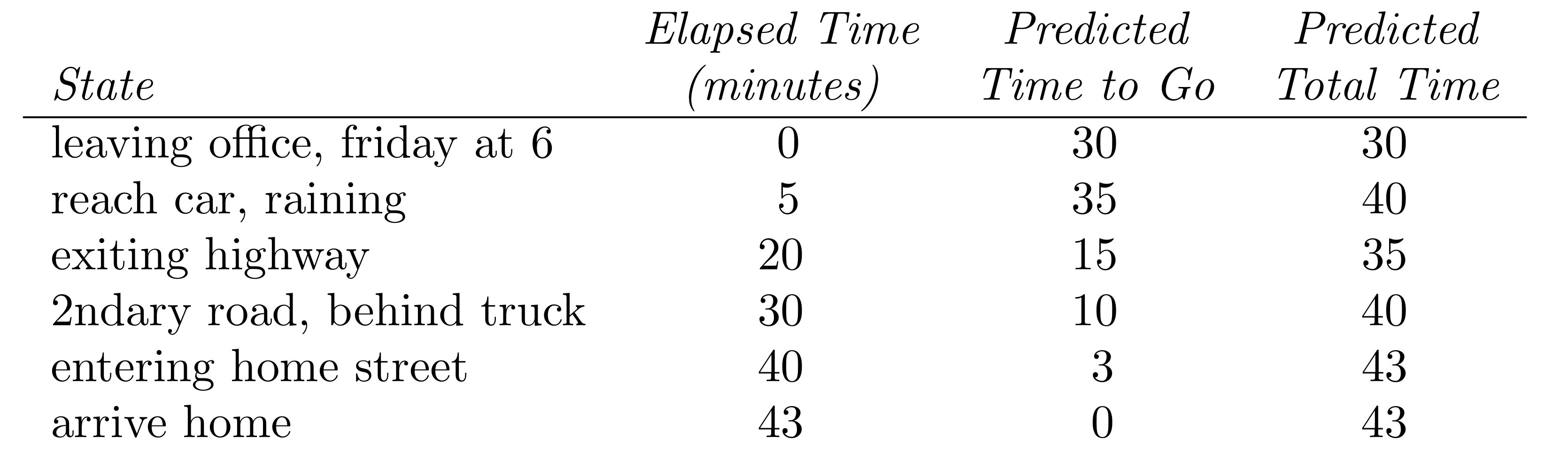
エピソードの実現値と価値の推定値

以下の表が各タイムステップtにおける，

• t期以前の累積報酬
• t期以降の期待報酬
• t期時点のエピソード期待総報酬

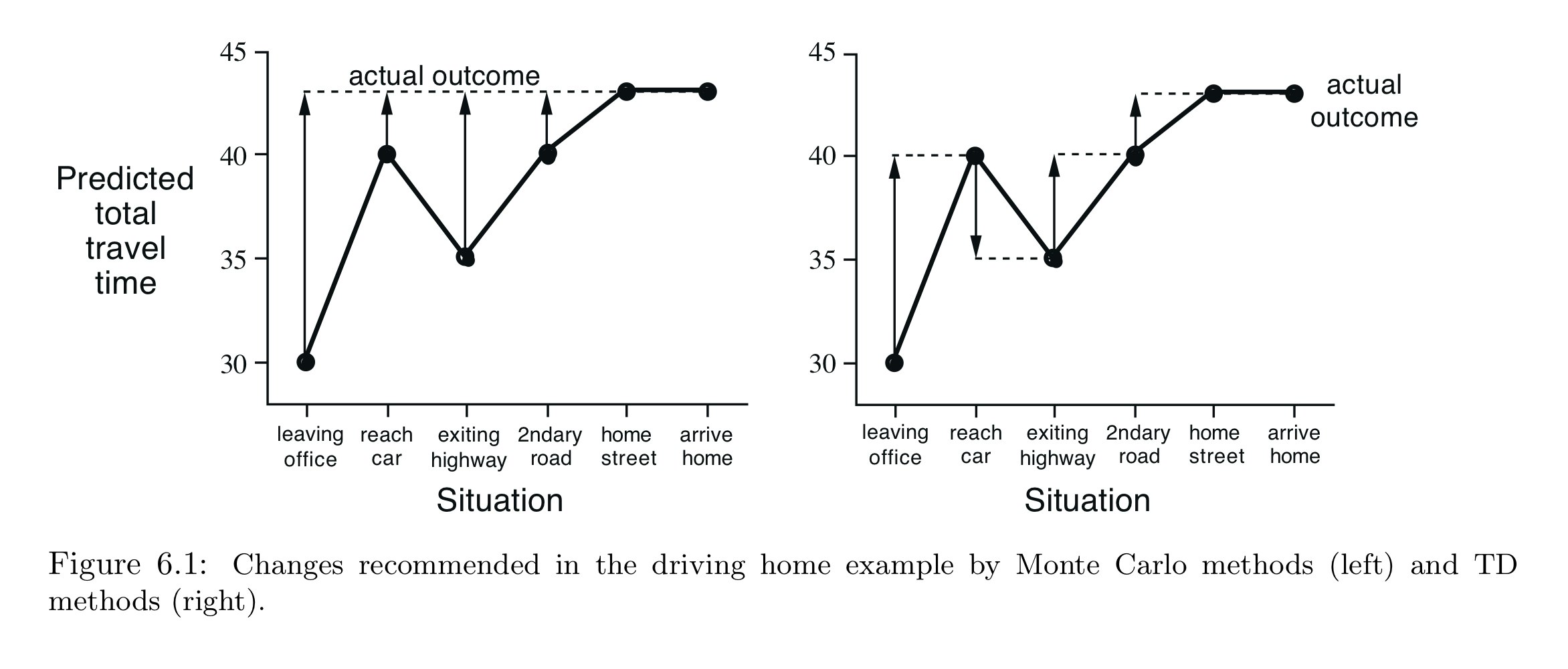
このエピソードを更新する操作は，

• Figure 6.1(左)：MC
• Figure 6.1(右)：TD

のように表される．

ただし，

• 横軸：タイムステップt
• 縦軸：タイムステップtにおいて期待される合計時間
• 矢印：$\alpha=1, \gamma=1$の場合の予測値の更新

を表す．

この図により推定値と実現値との誤差がわかる．
例えば、高速道路を降りたときにあと15分で帰れると思っていたが，実際には23分かかっている．
MCでは家についた時点で式(6.1)が適用され，高速道路を出た後の移動時間の推定値の増分を決定する．このときの誤差は$G_t - V(S_t)$は8分となる．
ステップサイズパラメータ$\alpha=1/2$だとすると、高速道路を出てからの予測は4分下方修正される．
(この場合はおそらく過剰反応/トラックはたぶん不運な故障)．
ただしこの更新は，家について実際のリターンが得られてからしかできない．

しかし，最終的な結果がわかるまで更新は待つ必要があるのだろうか？
仮に別の日にまた30分かかると想定してオフィスを出たとし，出てから25分後まだ高速道路にいてさらに25分かかると予想し直したとする．
このときすでに30分という最初の見積もりがかなり楽観的であったことを知っている．
ここでモンテカルロ法では，初期状態の推定値の更新は，家に着くまで待たなければならない．
一方，TD法ではすぐに学習し，最初の推定値を30分から50分に更新する($\alpha=1$の場合)．
この方法を先の例で考えると，Figure 6.1の右のようになる．

このように最後まで待っているよりも暫定の推定に基づいて学習する方が計算上有理であるため，一部を次のセクションで簡単に説明する．

6.2 Advantage of TD Prediction Method

TDの利点

DPやMCと比較したTD法の利点は以下である

• TD法 > DP法：

  • 環境のモデル、報酬と次の状態の確率分布を必要としない.

• TD法 > MC法：

  • オンラインで完全にインクリメンタルな方法で実装できる．(エピソードの最後まで待たなければならないのに対し、TD法では1タイムステップのみ待てば良い)
  • 以下のタスクに対して有効
    • 非常に長いエピソードを持つものタスク
    • エピソードが全くないタスク
  • 実験的な行動が取られたエピソードについて考慮する必要がない(その後にどのような行動が取られたかに関係なく，各遷移から学習するため)．

TD法の確かさ

実際の結果を待たずに次から次へと推測を学習するのは計算上簡単だが、正解への収束を保証できるかは自明でない．しかし，実は任意のポリシーπに対して、ステップサイズパラメータが十分に小さい定数の場合は、TD(0)では平均的に$v_{\pi}$に収束することが示される．また，ステップサイズが通常の確率的近似条件(2.7)に従って減少するとき、確率1で収束することが証明されている．
ほとんどの証明はテーブルベースの場合にのみであるが，線形関数近似の場合にも適用されることもある．これらの証明は第9章で議論する．

MC法とTD法の収束速度

MC法もTD法もどちらもが漸近的に正しい予測値に収束するならば，次はどちらが早く学習し，先に収束するかについて考えたくなる．しかし現時点では、どちらの方法が早く収束するかは数学的に証明できていない．ただ、ポリシーが確率的な場合、TD法は定数-αMC法よりも速く収束することが実験的にわかっている。

Example 6.2 Random walk

問題設定

• 以下の図のように遷移
• Cからスタート
• 等確率で左右に
• Eから右の終端に移動したときのみ報酬+1
• 真の価値は左から1/6ずつ増えていく

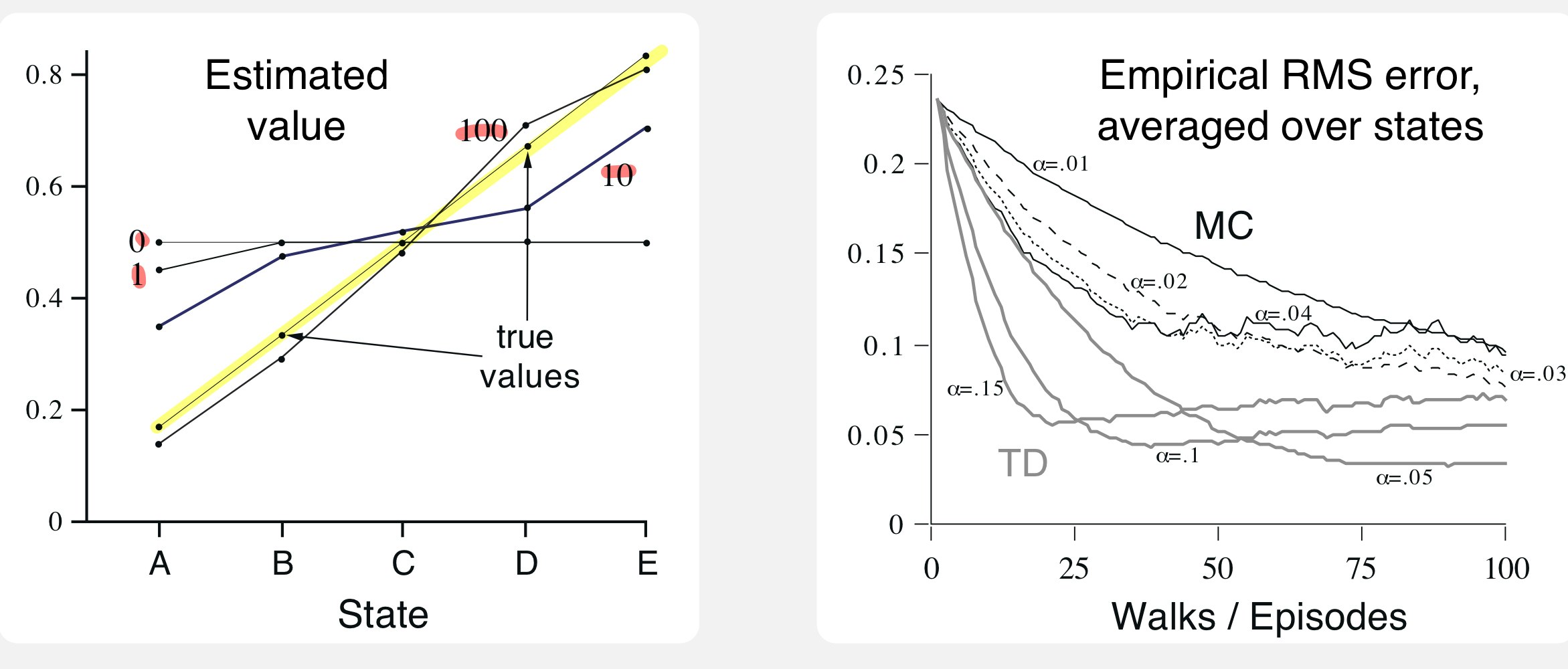
下左の図は，このポリシーでの状態価値をTD(0)で推定した結果を表す．($\alpha=0$, 100エピソード)
100エポック進むと真の価値(黄色)とほとんど一致していることがわかる．
また，下右の図はMC(黒)とTD(灰)の学習の様子を表す．ただし，縦軸は真の価値に対するRMSEを表す．
これよりTDの方が一貫してMCよりも早く収束していることがわかる．

6.3 Optimality of TD(0)

バッチ更新

10~100 くらいのエピソードしか持っていない場合を考える．
一般に使用可能なエピソードが少ない場合何度も繰り返し経験させる．
ここで各エピソードが終わった時点でそこまでで経験した全てのエピソードの経験を利用してまとめて更新するバッチ更新をした場合を考える．
これは各エピソードの各タイムステップで起きたことを記録しておき，1つのエピソードが終わった瞬間に記録してある分を全て利用して更新する方法である(これが計算上有効とは言ってない)．
バッチ更新をすれば定数$\alpha$が十分に小さい定数のとき確定的に最適値に収束する．

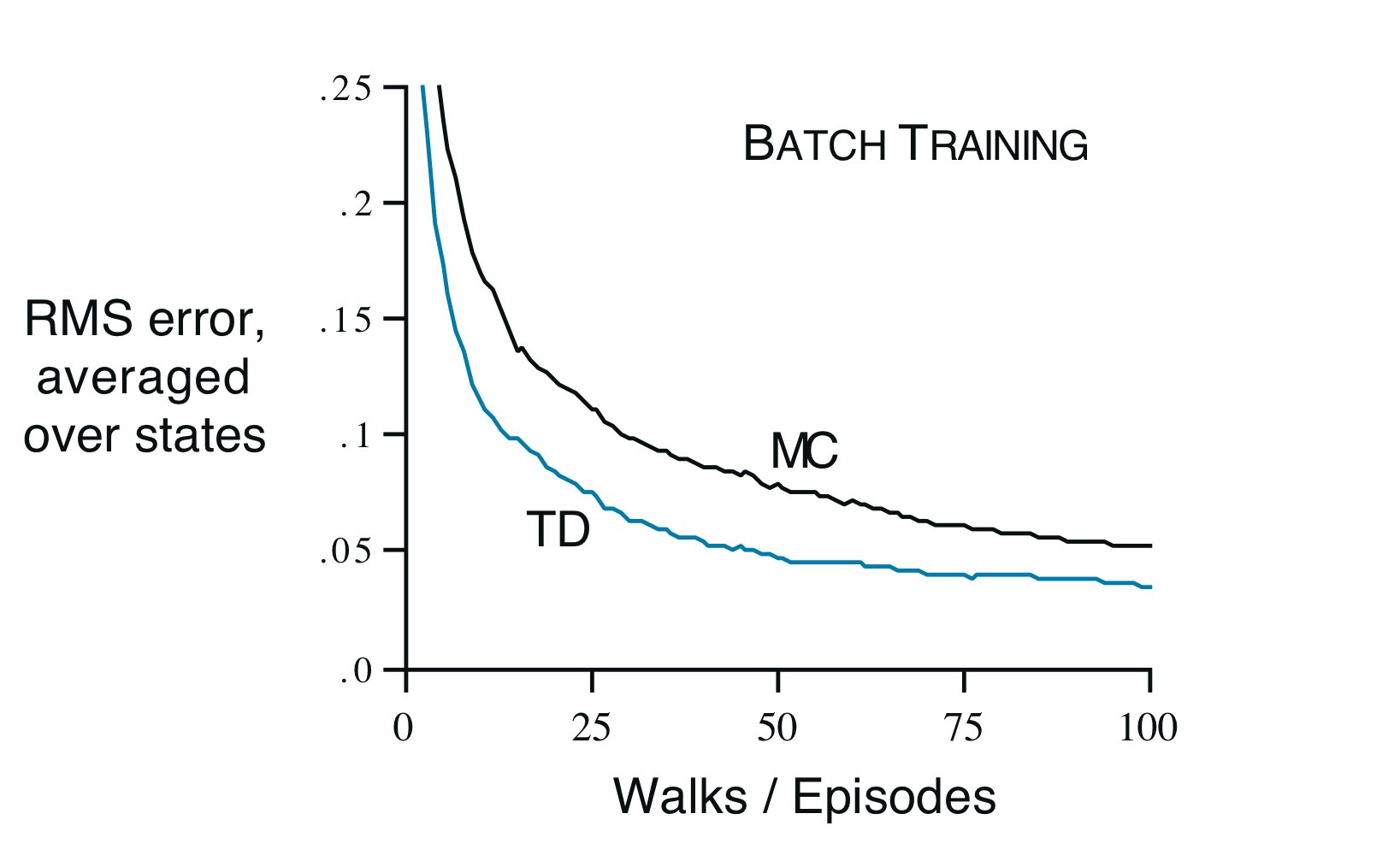
Example 6.3 Random walk under batch updating

Example 6.2のバッチ更新を考える．下の図がαを十分小さく設定した場合のMCとTDの結果を表す．これでもやはりMCよりTDが有効であることがわかる．

Example 6.4 You are the Predictor

設定

いま，マルコフ過程において,

• A,0,B,0
• B,1
• B,1
• B,1
• B,1
• B,1
• B,1
• B,0

という8つのエピソードとそのシークエンスが得られていたとする．
このときAとBの状態価値をどのように予測するだろうか？

考えられる予測

必ずBの次に終端し，確率3/4で1を獲得するため，Bの価値が3/4であることは推定できる．
しかし，Aについては二つ合理的な考え方がある．

• Aの次は100%BだからBと同じくAの価値は3/4
• Aを経験したエピソードは報酬が0の割合が100%だからAの価値は0

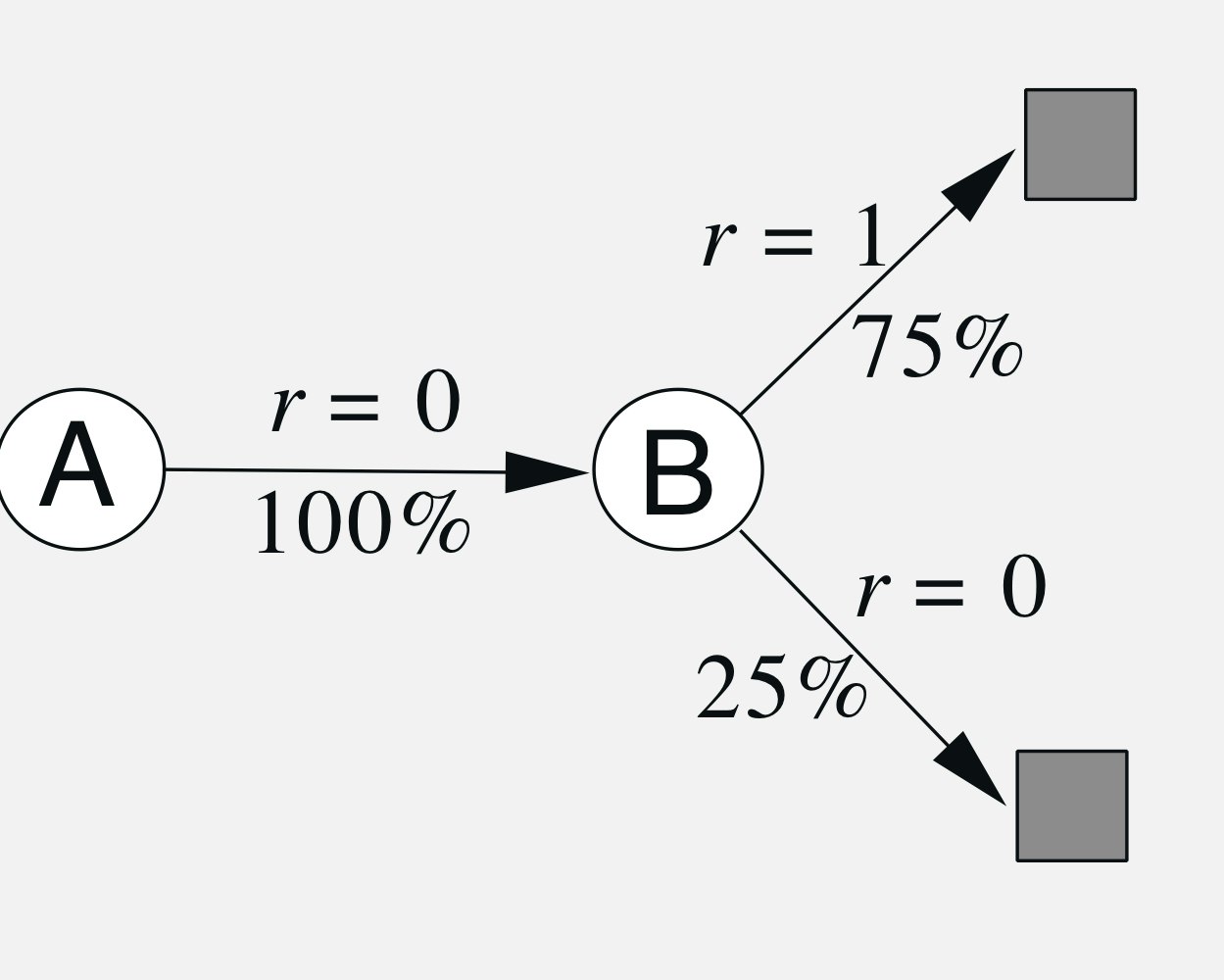
この二つの考えは正しくTDとMCの違いにある．
確かにどちらも合理的であるが，後者は訓練データのRMSEを0にする方法と言え，未来のデータに強いのは前者であると言える．

確実性等価推定値

以上の例はTD法とMC法の違いを示している．
($\alpha=1$のときは)MC法は訓練データのRMSEを最小にする一方で，TD法は毎バッチごとにiからjへの遷移確率と各遷移で得られる報酬を平均することで，MDPにおける最尤な推定値を求めている．モデルが一定であれば最尤推定はモデルと等価(確実性等価推定値, certainty-equivalence estimate)であり，バッチ更新のTD(0)は確実性等価推定値に収束すると言える．

オンラインのMCとTDの比較はできないが，オンラインのTDがMCより収束が早いのも，これが理由となっているかもしれない．つまり，MCは各エピソードでのエラーを0にするような方向に修正を行うが，TD法はより未来に起こる経験に対して汎化性能の高い方向に修正するため収束が早いと考えられる．
(ただし，最尤推定は$O(N^2)$であるのでオンラインTDでは最尤推定を行うことはなく，あくまでも近似であることに注意する.)

まとめ

• TD法はDPとMCの良いとこどり．
• TD(0)は平均的には最適解に収束する(9章で議論)．
• DPとは違って環境モデルを把握してなくて良い．
• MCよりも実験的に収束が早い(最尤推定に近いため？)．