はじめに
Pythonでt検定したい場合、 scipy.statsのttest_indを使うことが多いと思います。
基本的にはttest_indを使用すれば良いと思うのですが、この関数は全サンプルが必要になります。小規模のデータサイズなら何も考えず突っ込めば良いのですが、これが10~100万となったらしんどいですよね。というか、t検定では要約統計量(平均値や不偏分散など)のみが必要なので、わざわざ全サンプル用意するのは無駄な気がしてしまいます。
というわけで、準備するのが要約統計量だけで済むよう、t検定をPythonでスクラッチ実装してみます。scipyのttest_indと比較することで、妥当性を検証しようと思います。
2022.01.20追記
scipyで ttest_ind_from_stats という関数が実装されており、要約統計量を引数に渡すことでt検定の結果を得られます。
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind_from_stats.html
そもそもt検定とは?
母平均に対する検定。「グループA,Bの平均値の差」を検定する。
例えば、「A/Bテストを行った結果、Aグループの購買金額の平均は1000円、Bグループの購買金額の平均は1050円だった。この50円の差は偶然の産物なのか?どうなんだ???」ってときに使うイメージです。(違ったらツッコミください)
今回は対応のない2群のt検定を実装します。対応のある2群のt検定、1群のt検定は扱いません。
notebook
githubにコードをアップしています。
https://github.com/hatena-hanata/ml_stats_study/blob/master/stats/01_t_test.ipynb
実装
1. データセット
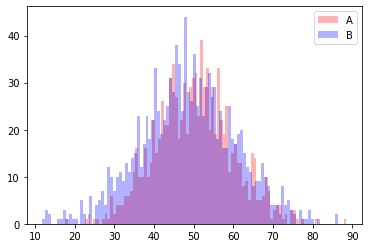
グループA:平均50、標準偏差10の正規分布から1000個ランダムサンプリングした標本
グループB:平均48、標準偏差12の正規分布から1200個ランダムサンプリングした標本 とします。
今回は正規分布からのランダムサンプリングとしましたが、標本数が大きければ、中心極限定理により標本平均の分布は正規分布に近付くので、標本の分布は正規分布でなくても大丈夫です(間違ってたらご指摘ください)。
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
m = 1000
n = 1200
a = np.random.normal(loc=50, scale=10, size=m)
b = np.random.normal(loc=48, scale=12, size=n)
plt.hist(a, bins=100, alpha=0.3, histtype='stepfilled', color='r', label='A')
plt.hist(b, bins=100, alpha=0.3, histtype='stepfilled', color='b', label='B')
plt.legend()
Aの平均値は50.19、Bの平均値は48.58となりました。このAとBの平均値の差が、統計的に有意か調べるのがt検定です。
2. Studentのt検定(等分散を仮定)
まずはじめに、等分散を仮定したStudentのt検定を実施します。
2-1. 各種統計量を求める
# a 平均と不偏分散
a_mean = a.mean()
a_var = a.var(ddof=1)
# b 平均と不偏分散
b_mean = b.mean()
b_var = b.var(ddof=1)
# poolした分散
s_2 = ((m - 1) * a_var + (n - 1) * b_var) / (m + n - 2)
# 自由度
dof = m + n - 2
2-2. t値、p値を求める
from scipy.stats import t
t_value = (a_mean - b_mean) / (np.sqrt(s_2 * (1/m + (1/n))))
dof = m + n - 2
p_value = min(t.cdf(t_value, dof), 1-t.cdf(t_value, dof)) * 2
print(f't値:{t_value} p値:{p_value}')
### output
### t値:3.4287178596465306 p値:0.0006176178409258437
2-3. Scipyのt検定
scipy.statsのttest_indを使用します。equal_var=Trueとすることで、Studentのt検定になります。
stats.ttest_ind(a, b)
### output
### Ttest_indResult(statistic=3.4287178596465306, pvalue=0.0006176178409258371)
自分で実装したものと、おおよそ値が一致しています!
3. Weltchのt検定(等分散を仮定しない)
今回のテーマとは関係ないですが、こんな記事を見つけました。
https://biolab.sakura.ne.jp/welch-test.html
等分散かどうかに関わらずWeltchのt検定を使用するのが良さそうです。実装しましょう。
3-1. 各種統計量を求める
Studentのt検定とWeltchのt検定の差異は、分散と自由度が異なることに由来します。
# a 平均と不偏分散
a_mean = a.mean()
a_var = a.var(ddof=1)
# b 平均と不偏分散
b_mean = b.mean()
b_var = b.var(ddof=1)
# 使用する分散
s_2 = a_var / m + b_var / n
# 自由度
dof = int((a_var / m + b_var / n)**2 / (((a_var/m)**2 / (m-1)) + ((b_var/n)**2 / (n-1))))
自由度は少し複雑ですね。
3-2. t値、p値を求める
from scipy.stats import t
t_value = (a_mean - b_mean) / np.sqrt(s_2)
p_value = min(t.cdf(t_value, dof), 1-t.cdf(t_value, dof)) * 2
print(f't値:{t_value} p値:{p_value}')
### ouput
### t値:3.490154519416705 p値:0.000492256894277121
3-3. Scipyのt検定
ttest_indにequal_var=Falseとすることで、Weltchのt検定になります。
stats.ttest_ind(a, b, equal_var=False)
### output
### Ttest_indResult(statistic=3.490154519416705, pvalue=0.0004922547773957867)
値がおおよそ一致していることが分かります。
関数化してみた
以上の処理を1つの関数にまとめてしまいます。
from scipy.stats import t
import numpy as np
def t_test(a_mean, a_var, a_n, b_mean, b_var, b_n, equal_var=True):
# Studentのt検定
if equal_var:
s_2 = ((a_n - 1) * a_var + (b_n - 1) * b_var) / (a_n + b_n - 2)
dof = a_n + b_n - 2
# Weltchのt検定
else:
s_2 = a_var / a_n + b_var / b_n
dof = int((a_var / a_n + b_var / b_n)**2 / (((a_var/ a_n)**2 / (a_n-1)) + ((b_var/b_n)**2 / (b_n-1))))
t_value = (a_mean - b_mean) / np.sqrt(s_2)
p_value = min(t.cdf(t_value, dof), 1-t.cdf(t_value, dof)) * 2
print(f'TtestResult(statistic={t_value}, pvalue={p_value})')
引数が多いので、使い勝手は正直微妙ですね^^;
まとめ
上の実装の過程を見てもらえれば分かる通り、平均値、不偏分散、サンプルサイズが分かればt検定を実施することができます。
DBの大規模データに対してSQLで要約統計量を計算→Pythonでt検定実施
上記の様な時には↑の関数が使えそうだなと思いました。
参考
https://bellcurve.jp/statistics/course/9427.html
https://bellcurve.jp/statistics/course/9936.html