eigen3を使ってみた備忘録

概要

任意精度対角化(密行列，疎行列)を追い求め，色々試してます．昨日eigenというライブラリーに出会い，今日インストールして使ってみたのでログとして記録．

任意精度対角化としてMpackは密行列のsymmetric, Hermiteクラスを対角化を実装していますが，疎行列はそもそもlapackで提供していないということもあり粗行列を効率的に解くことはできないようです．

色々調べていくとEigenというc++テンプレートライブラリーが密行列，粗行列の対角化を実行可能なようです．かつunsupportedのmpfrのライブラリーを使うとどうも任意精度で対角化できそうなので忘れないうちにeigenを使ったログを残す．

ログを残す主たる理由は私はc++ユーザーではなくすぐ忘れてしまいそうなので．

環境
ubuntu 14.04

install

メインページEigenのGet it からlatestをダウンロード，展開．

そもそもテンプレートライブラリーというものが何なのか理解していないが，Eigen getting startを読むとテンプレートライブラリーはmake installする必要はないようで，展開したディレクトリでプログラムを掛けばそれだけで動くようだ．

試しに展開したディレクトリ(EigenやREADME.mdがあるディレクトリー)でgetting startにあるサンプルプログラム

#include <iostream>
#include <Eigen/Dense>
using Eigen::MatrixXd;
int main()
{
  MatrixXd m(2,2);
  m(0,0) = 3;
  m(1,0) = 2.5;
  m(0,1) = -1;
  m(1,1) = m(1,0) + m(0,1);
  std::cout << m << std::endl;
}

をコンパイルしてみたが

$ g++ test.cpp　-o a.out
test.cpp:3:23: fatal error: Eigen/Dense: No such file or directory
compilation terminated.

とコンパイルが通らなかったので

#include "Eigen/Core"

としなければならなかった(Cでも同様な現象があった気がするが忘れてしまった)．

さらに任意精度計算をするために eigen の unsupported モジュールMPFRC++ Support module
のサンプル

#include <iostream>
#include <Eigen/MPRealSupport>
#include <Eigen/LU>
using namespace mpfr;
using namespace Eigen;
int main()
{
  // set precision to 256 bits (double has only 53 bits)
  mpreal::set_default_prec(256);
  // Declare matrix and vector types with multi-precision scalar type
  typedef Matrix<mpreal,Dynamic,Dynamic>  MatrixXmp;
  typedef Matrix<mpreal,Dynamic,1>        VectorXmp;
  MatrixXmp A = MatrixXmp::Random(100,100);
  VectorXmp b = VectorXmp::Random(100);
  // Solve Ax=b using LU
  VectorXmp x = A.lu().solve(b);
  std::cout << "relative error: " << (A*x - b).norm() / b.norm() << std::endl;
  return 0;
}

のinclude 下記のように修正

#include "unsupported/Eigen/MPRealSupport"
#include "Eigen/LU"

しコンパイルするも

$ g++ test.cpp -o a.out -lgmp -lmpfr
In file included from test.cpp:2:0:
unsupported/Eigen/MPRealSupport:15:22: fatal error: Eigen/Core: No such file or directory
compilation terminated.

してもエラーを出す．しょうが無いので， Eigen/ と unsupported/ を /usr/local/include/ 以下に sudo コピーすることで，サンプルプログラムを実行可能になった．

MPRealSupport

コンパイルする際にgmpとmpfrのライブラリーをリンクする必要があるのでMPRealSupport
のサンプルは下記のようにしてコンパイルする必要がある

g++ test.cpp -o a -lgmp -lmpfr

任意精度対角化の準備

行列
$$
A = \begin{pmatrix}
0 & 1 & 0\\
2 & 0 & 2\\
0 & 1 & 0
\end{pmatrix}
$$

の固有値は$\pm2 ,0$である． double 精度，例えば numpy (python)で解けば

>>> import numpy as np
>>> np.set_printoptions(precision=18)
array([ -2.000000000000000000e+00,  -1.732555071631836086e-16,
         1.999999999999999556e+00])

とな0固有値に誤差が伝播する．Mathematicaで機械精度の行列を対角化した場合も同様で

In[15]:= Eigenvalues@N@{{0,1,0},{2,0,2},{0,1,0}}//FullForm
Out[15]//FullForm= List[-2.`,1.9999999999999996`,-1.732555071631836`*^-16]

である． もちろんｎMathematicaは任意の精度で($\le\infty$)で対角化可能である(が速度が気になる).
eigen3 と mpfrc++を使って対角化するプログラムは

#include <iostream>
#include <Eigen/Eigenvalues>
#include <unsupported/Eigen/MPRealSupport>
#include <Eigen/Dense>
using namespace Eigen;

using namespace mpfr;

int main()
{
  // set precision to 256 bits (double has only 53 bits)
  mpreal::set_default_prec(53);
  // Declare matrix and vector types with multi-precision scalar type
  typedef Matrix<mpreal,Dynamic,Dynamic>  MatrixXmp;
  MatrixXmp A(3,3); 

  A(0,0) = 0;
  A(0,1) = 1;
  A(0,2) = 0;

  A(1,0) = 2;
  A(1,1) = 0;
  A(1,2) = 2;

  A(2,0) = 0;
  A(2,1) = 1;
  A(2,2) = 0;
  
  std::cout << A << std::endl;
    
  EigenSolver<MatrixXmp> es(A);
  std::cout << es.eigenvalues() << std::endl;

  return 0;
}

みたいな感じで書けば良いようで，実行結果は

$ g++ eigenvalues-mpfrc-min.cpp -o a -lgmp -lmpfr 
$ ./a 
0 1 0
2 0 2
0 1 0
          (-2,0)
           (2,0)
(-3.28269e-77,0)

と高精度で評価されていることが分かる．説明にあるように

  // set precision to 256 bits (double has only 53 bits)
  mpreal::set_default_prec(53);

とすると実行結果は

$ ./a 
0 1 0
2 0 2
0 1 0
         (-2,0)
          (2,0)
(1.77435e-16,0)

となりdouble程度の精度しかない．

興味深いことに 0 固有値のlapack (numpy)の結果と， 機械精度(double)のMathematicaの結果は精度範囲で一致している．
私の記憶が正しければMathematicaはlapack方で実装されていると思うので，同じ結果なのであろう．

一方eigen3は表示桁数を増大させる方法が分からないが見れる範囲で異なる値を持っている．
これは採用しているアルゴリズムが違うことに起因するのであろうか？

ちなみに，mpmath (python)でデフォルト精度(=仮数部16桁)で対角化すると

>>> import mpmath
>>> mpmath.eig(mpmath.matrix([[0,1,0],[2,0,2],[0,1,0]]))
([mpf('-1.9999999999999993'), mpf('1.6358461123585456e-16'), mpf('2.0')],

この結果も異なるので，これはこれで興味深い．

to do

MPRealSupportは名前から実数のみのサポートなのだろうか？複素数もサポートされているのだろうか？
そもそもc++を使い始めて半日．使い方がよくわかっていない．

また速度比較

(追記)

eigen, mpack, mathematica で対角化した際の速度を比較する．
mpackは解ける行列のクラスに制限があるので次の対称行列

$$
M=
\begin{pmatrix}
1&1&0&\cdots &0\\
1&1&1&\cdots &0\\
0&1&1&\cdots &0\\
&\vdots&&\ddots&\\
0&0&0&\cdots &1\\
\end{pmatrix}
$$
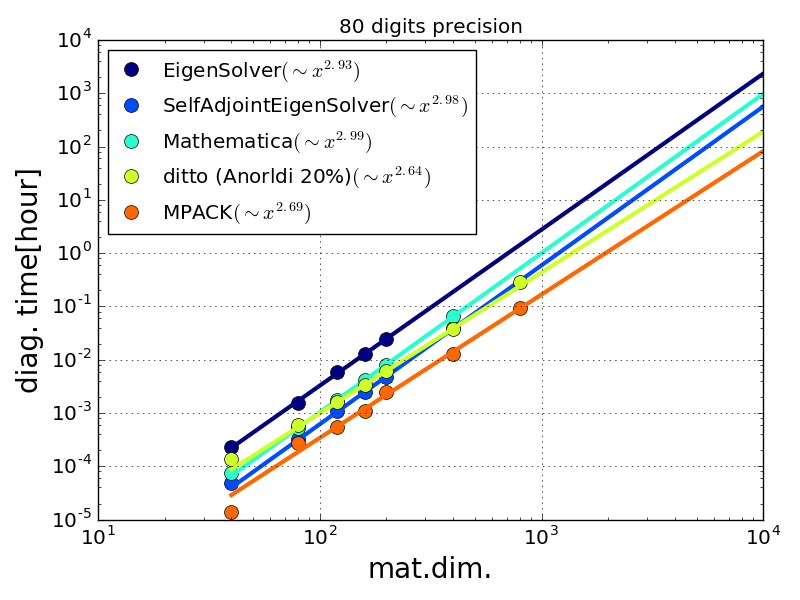
を80桁の精度で密行列として対角化する．

やはりMpack早い．mpackのプログラムを実行中cpuが400になるのでblasで並列化されているのだろう．
Eigenもblasが使えるようだがどうすれば良いのだろうか．

凡例の ditto (Anorldi 20%)のはmathematicaの対角化ルーチンであるEigensystemでAnorldi法(Lanczos法)を指定して固有値を大きい方を20%分求めたもの．

小さい方から求めた際の，比較はこれ

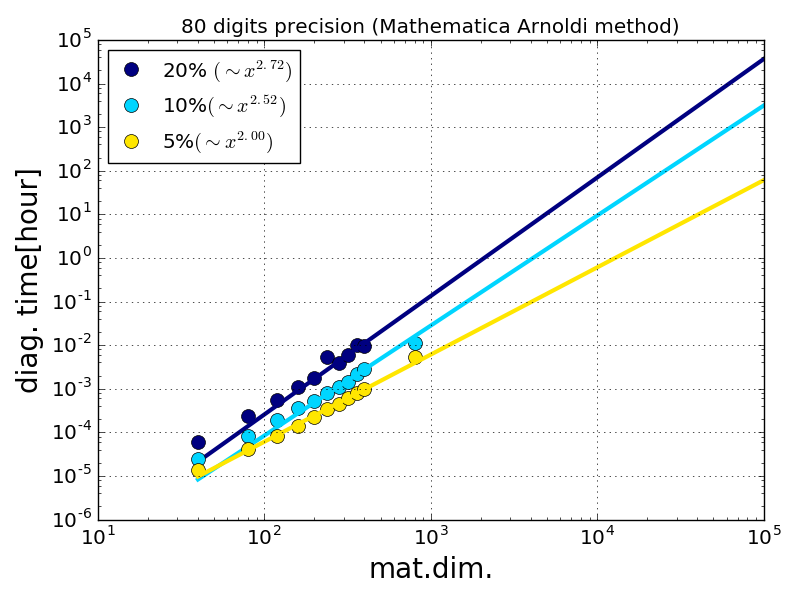
Arnoldi法やLanczos法であれば$10^5\times10^5$の対角化が現実味を帯びてくる．