動機&問題設定
勤め先でMatlabのライセンスが使える様になったので,matlabを使ってみたいということと,以前から気になっていたAdvanpix Multiprecision Computing Toolboxを用いた多倍長数値計算,特に一般(複素)行列の対角化利用してみる.なお,matlabは基本的なチュートリアルを小一時間触っただけなのでコードディングはいい加減だと思うことを断っておく.
AdvanpixのdocumentにあるCircus matrixと呼んでいるill-conditioned matrix
$$
\begin{equation}
A =
\begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 0 & 0 \\
-1 & 1 & 2 & 3 & 4 & 5 & 0 \\
0 & -1 & 1 & 2 & 3 & 4 & 5 \\
0 & 0 & -1 & 1 & 2 & 3 & 4 \\
0 & 0 & 0 & -1 & 1 & 2 & 3 \\
0 & 0 & 0 & 0 & -1 & 1 & 2 \\
0 & 0 & 0 & 0 & 0 & -1 & 1 \\
\end{pmatrix}
\end{equation}
$$
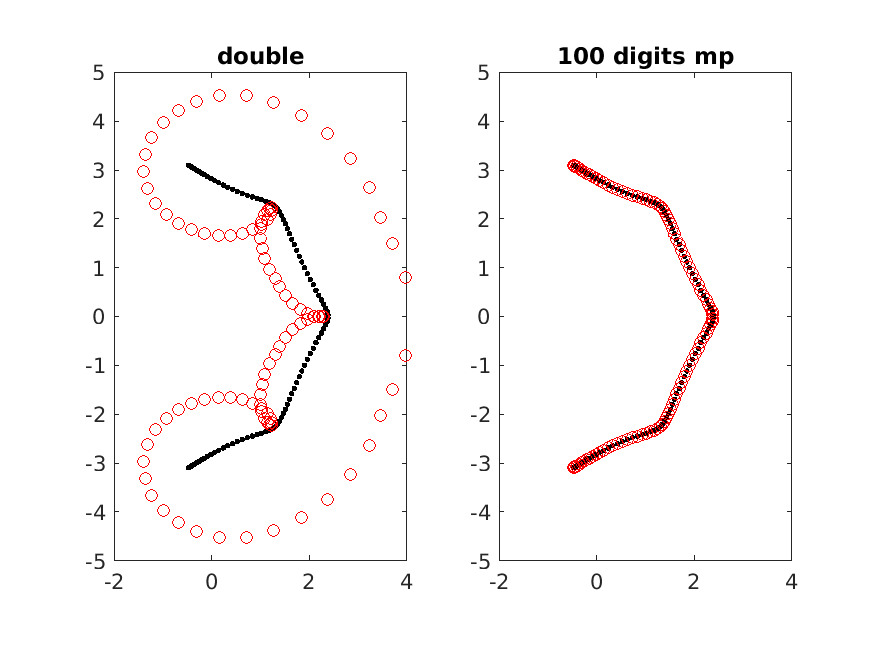
の非対称正方行列の次元を$n$とする(上の行列の場合は次元は7).これもAdvanpixのdocumentにある例題だが$n=100$の場合
addpath("AdvanpixMCT-4.8.0.14100");
mp.Digits(100);
n = 100;
A = toeplitz([1,-1,zeros(1,n-2)],[1:5,zeros(1,n-5)]);
B = toeplitz([1,-1,zeros(1,n-2, 'mp')],[1:5,zeros(1,n-5, 'mp')]);
figure
subplot(1,2,1)
plot(eig(A),'k.'), hold on, axis equal
plot(eig(A.'),'ro')
xlim([-2 4])
ylim([-5 5])
title('double')
subplot(1,2,2)
plot(eig(B),'k.'), hold on, axis equal
plot(eig(B.'),'ro')
xlim([-2 4])
ylim([-5 5])
title('100 digits mp')
fname = sprintf("matlab-eig-%d.png", n);
saveas(gcf, "eig-circus-mat.png");
を
$ matlab -batch circus_mat_eig
として実行する.
左はmatlabの倍精度,右はadvanpixの多倍長評価(100桁精度)の計算.非対称行列なので左右の固有値(A.':Aの転置)は一致する必要性はないが,この場合は一致するのだと思われる.そして,doubleの精度は全く信頼できないことが事がわかる.ill-condition matricesの世界は全く素人で,一般(複素)行列の多倍長精度対角化を実行するモチベーションは別の問題にあるものの,Circus matrixが良い例題なので,advanpixの評価を含めていくつかの言語と方法で評価してみる.
環境等
非対称正方行列の多倍長対角化が利用可能な幾つかのツール
- Matlab + advanpix
- Matlab + Symbolic Math Toolbox(SMT)
- Julia + GenericSchur,
- Mathematica (Wolfram言語),
- python + mpmath,
- python + flint (arb)
を使って対角化に要する時間を評価する.なお転置した行列も対角化すると時間が掛かるので右側固有値のみ計算する.ここでは計算速度に焦点を当てるので精度が十分かどうかは評価しない.なお仮数部を100桁,1000桁の2通り評価する.計算実行環境は
- intel core i9 9900k (8cores/16threads)
- intel xeon W-2195 (18cores/32threads)
である.
評価に使用したプログラムは本ページ下部かgithubに置いておく.
なお,arbにおける対角化 methodはexperimentalである.またnonstop mode=Trueにしないと精度が十分な場合,評価途中で終了するのでnonstop modeで走らせる.
なお,上述のツール以外に
- C++ Eigen
- C++ mpack (対称行列)
- Julia GenericLinearAlgebra (対称行列)
などが多倍長精度対角化を提供している.
評価
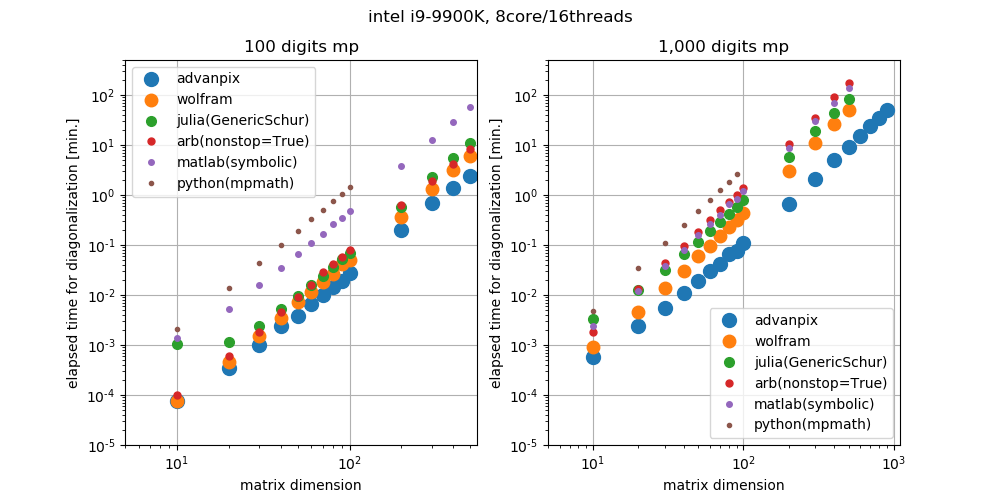
結論から言うとAdvanpixが唯一,非対称行列の対角化において並列化が実現しているので圧倒的に早い(但し,"AdvanpixMCT-4.8" version以降)
intel core i9 9900k
loglogだとどの程度早いのか分かりづらいのので代表的な実測値を表にした.
- intel core i9 9900k (8cores/16threads)
| dim (100 digits) | Advanpix[sec.] | Mathematica[sec.] | Julia[sec.] | Matlab(SMT)[sec.] |
|---|---|---|---|---|
| 100 | 1.65 | 2.99 | 4.15 | 29.1 |
| 500 | 142.0 | 365.5 | 665.0 | 3376.7 |
| dim (1,000 digits) | ||||
| 100 | 6.5 | 25.6 | 46.807 | 70.4 |
| 500 | 541.3 | 3048.4 | 5072.5 | 8413.6 |
1,000桁精度の場合はMathematicaと比較して5.6倍程度早い.
intel xeon W-2195
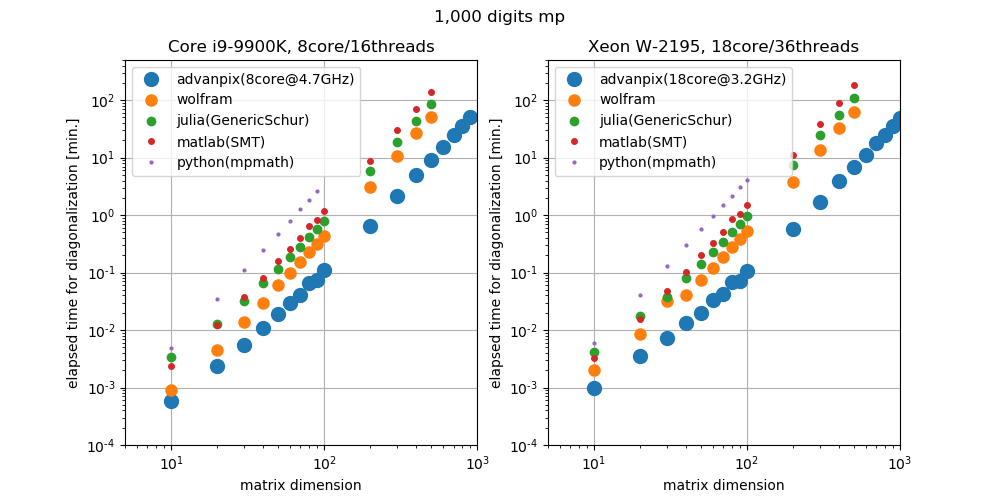
Advanpixが最も早い事がわかっているので
100桁精度の計算は省略してcore i9 9900k(8core@4700MHz)とxeon W-2195(18core@3200MHz)比較する.clock 周波数はi7zから読み取ったもの.
なお,python-flintがxeonマシンにインストールできなかったので除外した.
loglogだとどの程度早いのか分かりづらいののでAdvanpixの実測値を表にした.
| dim(1,000 digits) | W-2195[sec.] | i9-9900k[sec.] |
|---|---|---|
| 10 | 0.06 | 0.03 |
| 50 | 1.20 | 1.13 |
| 100 | 6.33 | 6.52 |
| 200 | 34.17 | 39.41 |
| 300 | 101.76 | 127.02 |
| 400 | 233.00 | 301.19 |
| 500 | 406.32 | 541.34 |
| 600 | 677.99 | 910.48 |
| 700 | 1063.33 | 1464.09 |
| 800 | 1511.90 | 2096.75 |
| 900 | 2147.55 | 3024.95 |
となり,行列次元が大きくなるとcore数による差が出てくる.
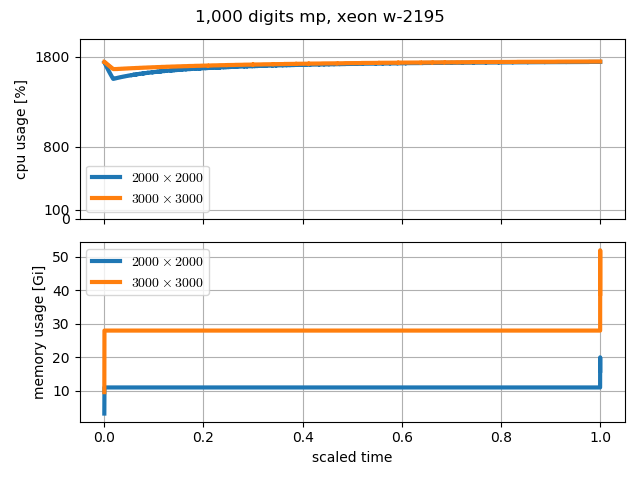
cpu & memory usage
対角化中のcpu & memory usageを計測する.cpuの使用率は他にcpu使用率70%を超えるプログラムが動いていない事を仮定してps コマンドからcpu使用率とmemory 使用率を取得する.
実際には下記bashスクリプトを使った
# !/bin/bash
n=0
while true; do
pid=$(ps ux --sort=-pcpu --no-headers | head -1 | awk '{print $2}')
cpu_usage=$(ps -o %cpu= $pid)
mem_usage=$(ps -o rss= $pid) # kbyte
if [ $(printf '%.0f' $cpu_usage) -gt 70 ]; then
echo $n $cpu_usage $mem_usage
n=`expr $n + 1`
sleep 1
fi
done
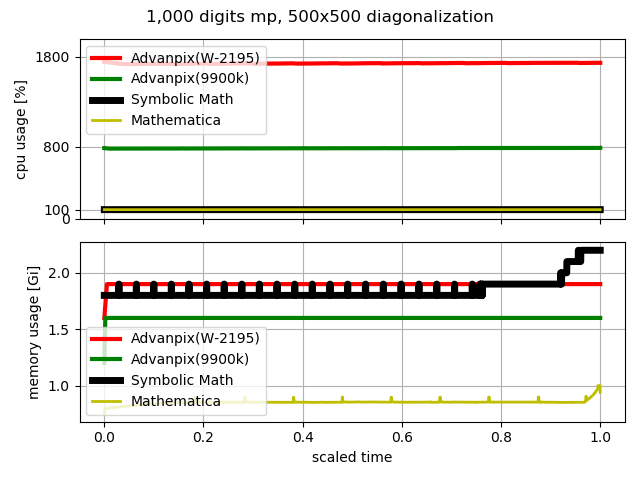
次の図にプログラム実行時におけるcpuとmemory使用率を示す.横軸のscaled time は 経過時間(every 1 sec.)/対角化に要した時間.Advanpix以外は対角化中のCPU usageは100%で固定されているが,Advanpixの場合は物理コア数$\times$100%で張り付いており対角化が終わるまで全物理コアを使っていることが分かる.
Mathematica や Symbolic Math toolboxは計算終了間際にmemory使用量が増大するが,その傾向はAdvanpixでも同じ.行列の次元が500程度ではほとんど変化を確認できないが,行列の次元を大きくすると,計算終了間際の数秒間でmemory 使用量が増大している事が分かる.
最後に計算に要する時間とメモリ使用量の予測値を示しておく.行列次元4000以上のmemory使用量は10分程度計算した際の使用量のみ実測している.
$10,000\times10,000$でも,計算に要する日数が60日程度なので現実的な範疇である.一方で,メモリ使用量はsemilog plotで線形なので指数関数で増えている傾向を示している.仮にfittingが正しいとすると$5000\times5000$行列は計算終了間際で1TB程度のmemoryを最後に要求してくることになる.最後の数秒~数分程度であればnvme ssdをcache(swap)として使えば計算は実行できそうだが,$10,000\times10,000$になると,1PBのメモリが必要になりそうなので現実的には不可能だろう.
以下対角化に要したプログラムを記載しておく.なおgithubにも置いておく.
追記
Advanpixの中の人に聞いたところ,プロセス終了時にメモリ使用率が肥大化するのはmatlabの external plugins/toolboxes (MEX) MEX仕様が原因のよう.c++でのpointerを直接matlabに渡す事ができない為,データの物理的なコピーをしなければならい事が原因のようだ.よって少なくとも2倍のmemoryを用意しておけば十分かもしれない.
中の人曰く,この問題を解決する方法を発見(MEXにはundocumented-functionが沢山あるらしい)したようだが,ソースをゼロから作成し直すことになるのですぐにはできないとのことだった.
Matlab + Advanpix
addpath("/AdvanpixMCT-4.8.0.14100/");
dps = 1000;
[ret, host] = system('hostname');
host = erase(host,char(10));
mp.Digits(dps);
format longG;
eps('mp')
savepath = host + "_advanpix/";
if ~exist(savepath, 'dir')
mkdir(savepath);
end
fname = sprintf(savepath + "mp%d-eig-time2.dat", dps);
of = fopen(fname, "w");
for dim = [10:10:100, 200:100:500]
A = toeplitz([1,-1,zeros(1,dim-2,'mp')],[1:5,zeros(1,dim-5,'mp')]);
tic;
[V1, D1]=eig(A);
eltime = toc;
fprintf("%d\t%f\n", dim, eltime);
fprintf(of, "%d\t%f\n", dim, eltime);
end
fclose(of);
version等
<<< ver
MATLAB バージョン: 9.8.0.1359463 (R2020a) Update 1
...
mp.Info()
-------------------------------------------------------------------------------------------------------------
Multiprecision Computing Toolbox, (c) 2008-2020 Advanpix LLC.
Version : 4.8.0 Build 14100
Release : 2020-06-11
...
advanpixについて
Advanpixは中の人の一人(?)はmpfrのc++ interfaceであるmpfrc++を実装された方のようだ.Advanpixの評価版使用時には,優位な差が無かった(cpu usage が100-400%の間で揺らぐ)ものの,開発者とのやり取りしていると2週間足らずで完全に並列化対応してしまう凄まじい方.更に一般化固有値問題も並列化対応したとのことで,本当に敬意と尊敬の念を抱く.いつの日か自分でそのような実装出来るようになりたいものである.
なお価格は
| Academic Single User License | $249 |
|:--|:--|--:|
| Industrial Single User License | $996 |
であり,これ以外評価版とmulti-computer licenseがあり,横浜に本社があるようだ.
なお,私は回し者ではなく単なる(利害関係のない)ユーザーであるのであしからず.
幾つかの備忘録
matlab初心者なので幾つかつまずいた事を記録しておく.
matlabはファイル命名規則が厳しくて,ハイフンなどの演算子記号は使えない.
matlabを実行する場合のオプションが結構複雑.matlabをterminal(bash)コマンドライン上の対話環境を起動する場合は
$ matlab -nojvm
但し,幾つかのjavaを必要とする機能が使用できなくなる(parallel computing toolboxなど)ので
$ matlab -nodisplay -nosplash -nodesktop
を使えば,対話環境であってもjvmが使えるようだ.
スクリプト(hoge.m)のフォアグランドでの実行は拡張子を除いて
$ matlab -batch hoge
とすれば実行できる.一方
$ nohup matlab -batch hoge &
のようにして,バックグランドで実行させ,logoutするとスクリプトが停止してしまう.
$ nohup matlab -nodisplay -nosplash -nodesktop -r hoge &
とするとhogeを実行したあとに,matlabのコマンドライン起動し続けるため無限ループに陥る.そしてnohup.oug(log)が
Warning: "Error reading character from command line"などの警告でで溢れる.これを回避するためには
nohup matlab -nodisplay -nosplash -nodesktop -r "run('hoge');exit" &
でスクリプトで強制的に終了させるか,同じことだが プログラム終了時に/dev/nullを呼ぶように
nohup matlab -nodisplay -nosplash -nodesktop -r hoge < /dev/null &
とすればbackground jobとして走らせ続ける事が出来る.
Matlab + Symbolic Math Toolbox
Symbolic Math Toolboxを使うとmachine epsilonの出力ができなかったので,1/3桁数からなんとなく精度を読みとっている
dps = 1000
digits(dps);
[ret, host] = system('hostname');
host = erase(host,char(10));
savepath = host + "_matlab/";
if ~exist(savepath, 'dir')
mkdir(savepath);
end
fname = sprintf(savepath + "mp%d-eig-time.dat", dps);
of = fopen(fname, "w");
for dim = [10:10:100, 200:100:500]
disp(vpa(1/3));
disp(strlength(sprintf("%s", vpa(1/3))));
A = vpa(toeplitz([1,-1,zeros(1,dim-2)],[1:5,zeros(1,dim-5)]));
tic;
[V1, D1]=eig(A);
eltime = toc;
fprintf("%d\t%f\n", dim, eltime);
fprintf(of, "%d\t%f\n", dim, eltime);
end
fclose(of);
version
Symbolic Math Toolbox バージョン 8.5 (R2020a)
Wolfram(Mathematica)
特にコメントはない.
dps=1000;
circus[dim_]:=Module[{a,b},
a = {1,-1}~Join~ConstantArray[0,dim-2];
b = Range[5]~Join~ConstantArray[0,dim-5];
ToeplitzMatrix[a, b]
]
savepath = $MachineName <> "_wolfram/"
If[Not@DirectoryQ[savepath], CreateDirectory[savepath]];
of = OpenWrite[ savepath <> "mp"<>ToString[dps]<>"-eig-time.dat"];
dims = Range[10, 100, 10] ~Join~ Range[200, 500, 100];
Table[
path = savepath <> "mp" <>ToString[dps]<> "-load-mem-dim"<>ToString[dim]<>".dat";
m = circus[dim];
tic=AbsoluteTime[];
{evals1, evecs1} = Eigensystem[N[m,dps]];
toc = AbsoluteTime[] - tic;
Print@{dim, toc};
Export[of, {{dim, toc}}];
Export[of, "\n"],
{dim, dims}
]
version
wolfram
Mathematica 12.0.0 Kernel for Linux x86 (64-bit)
julia + GenericSchur
GenericLinearAlgebraで対角化可能なハミルトニアンはHermite(対称行列)に限られるようなのでGnericSchurを使う.ただし,行列の要素をBigIntにするとmethod errorとなるため,BigFloatにしている.また,circus matrixの作成はかなり手抜き.
# using GenericLinearAlgebra
using Dates
using GenericSchur
setprecision(3323) # 1,000 digits mp
# setprecision(333) # 100 digits mp
function circus(n::Int64)
t = BigFloat
A = zeros(t, n, n)
B = zeros(t, n, n)
a = [1:5; zeros(t, n-5)]
b = [-1; 1:5; zeros(t, n-6)]
A[1,:] = a
for i = 2:n, j=i-1:n
c = circshift(b,i-2)
A[i,j] = c[j]
end
A
end
epsilon = eps(BigFloat(1))
println(epsilon)
dps = round(Int, -log10(epsilon))
println(dps)
savepath = gethostname() * "_julia/"
if ~isdir(savepath)
mkdir(savepath)
end
of = open(savepath * "mp$dps-eig-time.dat", "w")
for dim=[10:10:100; 200:100:500]
A = circus(dim)
tic = now()
S = GenericSchur.gschur(A)
toc = now() - tic
time = toc.value / 1000
println("$dim \t $time")
write(of, "$dim \t $time\n")
flush(of)
end
close(of)
version
julia> versioninfo()
Julia Version 1.3.1
Commit 2d5741174c (2019-12-30 21:36 UTC)
Platform Info:
OS: Linux (x86_64-pc-linux-gnu)
CPU: Intel(R) Xeon(R) W-2195 CPU @ 2.30GHz
WORD_SIZE: 64
LIBM: libopenlibm
LLVM: libLLVM-6.0.1 (ORCJIT, skylake)
(v1.3) pkg> status GenericSchur
Status `~/.julia/environments/v1.3/Project.toml`
[c145ed77] GenericSchur v0.4.0
python + mpmath
特にコメントはない.
mport numpy as np
import matplotlib.pyplot as plt
import scipy.linalg
import mpmath
import time, os
mpmath.mp.dps = 1000
savepath = os.uname()[1] + "_python/"
if not os.path.exists(savepath):
os.mkdir(savepath)
of = open(savepath + "mp%d-eig-time.dat" % mpmath.mp.dps, "w")
for dim in range(10, 110, 10):
a = np.concatenate(( [1,-1], np.zeros(dim-2,dtype=int) ))
b = np.concatenate(( np.arange(1,6), np.zeros(dim-5, dtype=int) ))
m = mpmath.matrix(scipy.linalg.toeplitz(a, b))
tic = time.time()
evals0, evecs0 = mpmath.mp.eig(m)
toc = time.time() - tic
print(dim, toc)
of.write("%d\t%f\n" % (dim, toc))
of.flush()
of.close()
version
$ conda info
active environment : None
conda version : 4.8.2
conda-build version : 3.17.8
python version : 3.7.3.final.0
virtual packages : __glibc=2.28
platform : linux-64
user-agent : conda/4.8.2 requests/2.20.1 CPython/3.7.3 Linux/4.19.0-8-amd64 debian/10 glibc/2.28
UID:GID : 1000:1000
netrc file : None
offline mode : False
In [1]: import mpmath
In [2]: mpmath.__version__
Out[2]: '1.1.0'
python + flint + arb
flintもarbはあまりつかったことがないので説明できないが,arbは非対称行列の対角化をexperimentalとして実装しているようだ.
import numpy as np
import flint
import scipy.linalg
import time, os
flint.ctx.dps = 1000
# flint.ctx.threads = 8
savepath = os.uname()[1] + "_python_arb/"
if not os.path.exists(savepath):
os.mkdir(savepath)
of = open(savepath + "mp%d-eig-time.dat" % flint.ctx.dps, "w")
dims = np.append(np.arange(10, 100, 10), np.arange(100, 600, 100))
for dim in dims:
a = np.concatenate(( [1,-1], np.zeros(dim-2,dtype=int) ))
b = np.concatenate(( np.arange(1,6), np.zeros(dim-5, dtype=int) ))
m1 = scipy.linalg.toeplitz(a, b)
CM1 = flint.arb_mat(m1.tolist())
tic = time.time()
[evals1, evecs1] = CM1.eig(left=True, nonstop=True)
toc = time.time() - tic
print(dim, toc)
of.write("%d\t%f\n" % (dim, toc))
of.flush()
of.close()
version
$ pip search python-flint
python-flint (0.3.0) - Bindings for FLINT and Arb
INSTALLED: 0.3.0 (latest)
...