背景
前回の投稿から約二年強.前回のいろんな言語を雑に実装して計算速度の比較を行った.そのモチベーションには任意精度計算で計算速度の比較を行いたいという伏線がある.
任意精度計算は,GNU MP(GMP), MPFR (何れもC,C++)の実装がメジャーで,これらのパッケージのwrapperや拡張がいつくかの言語で利用可能である.
pythonではmpmathで利用可能(標準ライブラリーのDecimalは知らない)で,juliaやMathematica(wolfram言語)ではdefaultで多倍長演算をサポートしている.何れもGMPやMPFRを利用しているようなので,実装によるオーバーヘッドやコーディングの平易さがどの程度なものなのか知りたいというのが,最終的な目的である(今回は到達しない).
ちなみに,gcc 4.6 から4倍精度計算がサポートされ,C,C++,Fortranでは4倍精度演算も可能なはずだがここでは扱わない.
(Cでは,4倍精度浮動小数点型は __float128 とい取って付けたような宣言が必要だったが今はどうなんだろうか・・・.)
任意精度が必要な例
(1次元の)パイコネ変換(baker's map)
$$
B(x) =
\begin{cases}
2x,& 0 \le x \le 1/2 \\
2x-1,& 1/2 < x \le 1
\end{cases}
$$
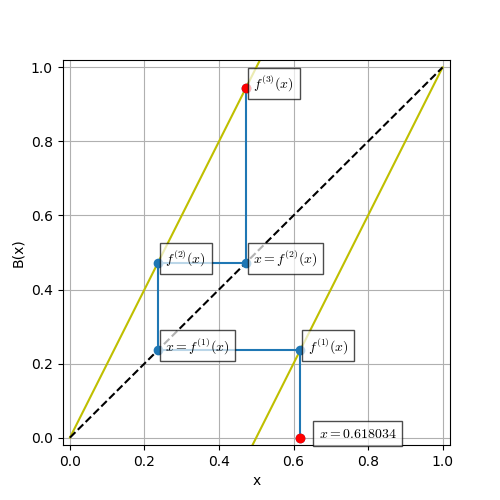
を考える$x\in[0,1]$を初期条件として,$B$の反復合成によって得られる軌道列$\{x, B(x), B^{(2)}=B\circ B(x),\ldots, B^{(n)}(x)\}$を考えるとこれはカオス的に振る舞う(Bの操作でパンは均一にコネられるよ).
とりあえず,適当な初期条件を与えて3階までの反復を描画するコードを(雑に)書く.
import numpy as np
import matplotlib.pyplot as plt
import time
def B(x):
return 2*x if x <= 1/2 else (2*x - 1)
fig, ax = plt.subplots(1, 1, figsize=(5,5))
ax.set_xlabel("x")
ax.set_ylabel("B(x)")
x = np.linspace(0, 1, 300)
ax.set_ylim(-0.02,1.02)
ax.set_xlim(-0.02,1.02)
ax.plot(x,2*x,"-y")
ax.plot(x,2*x-1,"-y")
ax.plot(x,x,"--k")
x = (np.sqrt(5) - 1)/2
web = [np.array([x]),
np.array([0])]
traj = np.array([x])
nmax = 3
bboxprop = dict(facecolor='w', alpha=0.7)
ax.text(x+0.05,0, r"$x=%f$" % x, bbox=bboxprop)
a = time.time()
for n in range(1,nmax+1):
y = B(x)
web[0] = np.append(web[0], x)
web[1] = np.append(web[1], y)
traj = np.append(traj, y)
ax.text(x+0.02, y, r"$f^{(%d)}(x)$" % n, bbox=bboxprop)
x = y
if n != nmax:
ax.text(y+0.02, y, r"$x=f^{(%d)}(x)$" % n, bbox=bboxprop)
web[0] = np.append(web[0], x)
web[1] = np.append(web[1], y)
print(time.time() - a, "[sec.]")
ax.plot(web[0][:], web[1][:], "-o")
ax.plot(web[0][0], web[1][0], "or")
ax.plot(web[0][-1], web[1][-1], "or")
ax.grid()
print(traj)
plt.savefig("web.png")
plt.show()
を実行すれば$\{x, B(x), B\circ B(x), B\circ B\circ B(x)\}$の軌道列が得られ,
$ python baker.py
0.0013127326965332031 [sec.]
[0.61803399 0.23606798 0.47213595 0.94427191]
また図(web diagramあるいはphase portrait)は反復合成の意味を視覚的に理解出来ると思う(始点と終点を赤丸にしている).
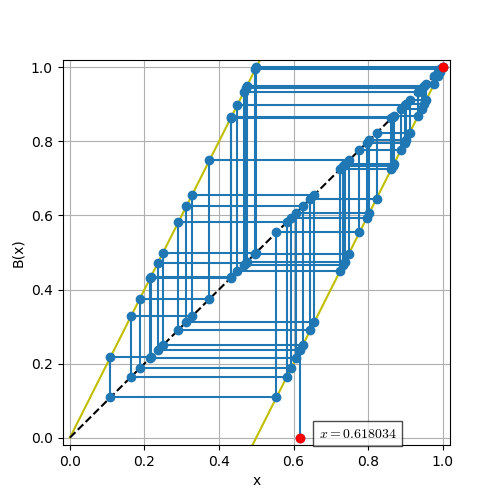
さて,反復の回数を50にするとどうなるだろうか.
nmax = 3
を
nmax = 50
にして実行すると
$ python baker-2.py
0.0012233257293701172 [sec.]
[0.61803399 0.23606798 0.47213595 0.94427191 0.88854382 0.77708764
0.55417528 0.10835056 0.21670112 0.43340224 0.86680448 0.73360896
0.46721792 0.93443584 0.86887168 0.73774336 0.47548671 0.95097343
0.90194685 0.8038937 0.60778741 0.21557482 0.43114964 0.86229928
0.72459856 0.44919711 0.89839423 0.79678845 0.59357691 0.18715382
0.37430763 0.74861526 0.49723053 0.99446106 0.98892212 0.97784424
0.95568848 0.91137695 0.82275391 0.64550781 0.29101562 0.58203125
0.1640625 0.328125 0.65625 0.3125 0.625 0.25
0.5 1. 1. ]
の結果がえられた.
定義より$B(1) = 1$なので,初期条件 $x = (\sqrt{5} -1 )/2$とした十分長い反復合成$B^{(n)}(x)$は1に収束すると数値計算から予想される(パンが均一に混ざらない・・・.)
しかし数値計算に基づくこの予想は計算精度が不十分であるために誤って導かれたものである.
この系は特別な初期条件($x=0,1/2,1$など)を除きほとんど全ての初期点に対する時系列はカオス的に振る舞い,$x \in [0,1]$を稠密に埋める.
このことを確認するために,python の任意精度packageであるmpmathを用いて同じ計算を実施する.
import numpy as np
import matplotlib.pyplot as plt
import mpmath
import time
mpmath.mp.dps = 100
def B(x):
return 2*x if x <= 1/2 else (2*x - 1)
fig, ax = plt.subplots(1, 1, figsize=(5,5))
ax.set_xlabel("x")
ax.set_ylabel("B(x)")
x = np.linspace(0, 1, 300)
ax.set_ylim(-0.02,1.02)
ax.set_xlim(-0.02,1.02)
ax.plot(x,2*x,"-y")
ax.plot(x,2*x-1,"-y")
ax.plot(x,x,"--k")
x = (np.sqrt(5) - 1)/2
web = [np.array([x]),
np.array([0])]
traj = np.array([x])
x = (mpmath.sqrt(5) - 1)/2
y = B(x)
web = [np.array([x]),
np.array([0])]
traj = np.array([x])
nmax = 50
a = time.time()
for n in range(1,nmax+1):
y = B(x)
web[0] = np.append(web[0], x)
web[1] = np.append(web[1], y)
traj = np.append(traj, y)
x = y
if n!=nmax:
web[0] = np.append(web[0], x)
web[1] = np.append(web[1], y)
print(time.time() - a, "[sec.]")
ax.plot(web[0], web[1], "-o")
ax.plot(web[0][0], web[1][0], "or")
ax.plot(web[0][-1], web[1][-1], "or")
ax.grid()
mpmath.nprint(traj.tolist())
plt.savefig("web-mp1.png")
plt.show()
本質的な変更は
import mpmath
mpmath.mp.dps = 100
と初期条件
x = (mpmath.sqrt(5) - 1)/2
だけである.mpmath.mp.dps = 100は仮数部100桁の精度で評価を行う様に指定する.
(デフォルトではdoubleの精度(15)が指定されている.)
print(traj)だと100桁そのまま出力されるので,mpmathのtrajを一度リストに変換しnprintを使って表示桁数を少なくする.
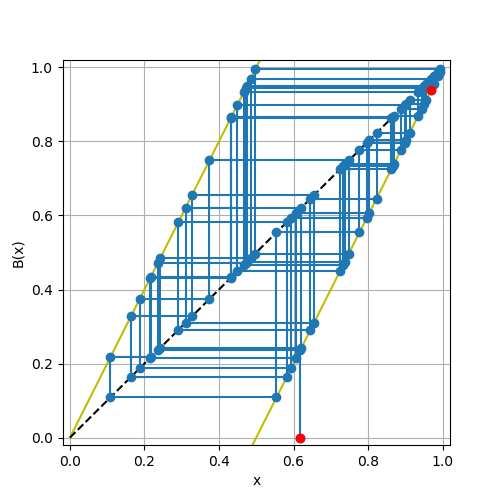
出力結果は
$ python baker_mp.py
0.0019168853759765625 [sec.]
[0.618034, 0.236068, 0.472136, 0.944272, 0.888544, 0.777088, 0.554175, 0.108351, 0.216701, 0.433402, 0.866804, 0.733609, 0.467218, 0.934436, 0.868872, 0.737743, 0.475487, 0.950973, 0.901947, 0.803894, 0.607787, 0.215575, 0.43115, 0.862299, 0.724599, 0.449197, 0.898394, 0.796788, 0.593577, 0.187154, 0.374308, 0.748615, 0.49723, 0.994461, 0.988921, 0.977842, 0.955685, 0.911369, 0.822739, 0.645478, 0.290956, 0.581912, 0.163824, 0.327647, 0.655294, 0.310589, 0.621177, 0.242355, 0.48471, 0.96942, 0.93884]
倍精度の計算結果とは異なり,50stepでは1に収束しない.
計算速度は若干遅くなるものの許容範囲である.さらに長く時間発展してみようnmax = 350として時間発展してみよう
出力もstep数に応じて長くなるので最後30ステップ以降を表示すると
mpmath.nprint(traj.tolist()[-30:])
$ python baker_mp.py
0.013526201248168945 [sec.]
[0.0256348, 0.0512695, 0.102539, 0.205078, 0.410156, 0.820313, 0.640625, 0.28125, 0.5625, 0.125, 0.25, 0.5, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]
となる.仮数部100桁の計算でもステップ数が十分長くなれば1に漸近するように見える.
更に精度を良くするとどうなるであろうか.
mpmath.mp.dps = 200
として実行する.
$ python baker_mp.py
0.013622760772705078 [sec.]
[0.0256048, 0.0512095, 0.102419, 0.204838, 0.409676, 0.819353, 0.638705, 0.27741, 0.55482, 0.109641, 0.219282, 0.438564, 0.877127, 0.754255, 0.50851, 0.017019, 0.0340381, 0.0680761, 0.136152, 0.272304, 0.544609, 0.0892179, 0.178436, 0.356872, 0.713743, 0.427487, 0.854974, 0.709947, 0.419894, 0.839788]
今度は1に漸近する様子は見られなかった.長時間の時間発展を正確に得るためには精度を高くしなければならない.
幾つかの実装による計算速度比較
上の例の実装はnp.appendを使用しているため,計算速度が極めて遅くなる.
私の環境で
mpmath.mp.dps = 100000
nmax = 10000
で実行すると
$ python baker_mp.py
1.895829439163208 [sec.]
[0.170384, 0.340767, 0.681535, 0.36307, 0.72614, 0.452279, 0.904559, 0.809118, 0.618235, 0.236471, 0.472941, 0.945882, 0.891765, 0.78353, 0.56706, 0.13412, 0.26824, 0.536479, 0.0729585, 0.145917, 0.291834, 0.583668, 0.167335, 0.334671, 0.669341, 0.338683, 0.677365, 0.35473, 0.70946, 0.418921]
2秒弱掛かる.appendは便利だが,配列の再取得を繰り返す(malloc, copyを繰り返す)ような操作なので遅い.
必要な配列を先に準備しておき,代入操作だけで完結させれば.早くなるはずである.
mpmathは行列のclassが定義されているのでそれを使ってみる.ただし,1次元配列に相当するものpython のlistなので,listの場合とnumpy.arrayの場合も比較してみる.変更有る箇所だけ示すと次のようなコード
nmax = 10000
web = mpmath.zeros(2*nmax+1,2)
web[0,0] = x
web[0,1] = 0
traj = [mpmath.mpf("0")]*(nmax+1)
traj[0] = x
a = time.time()
for n in range(1,nmax+1):
y = B(x)
web[2*n - 1, 0] = x
web[2*n - 1, 1] = y
traj[n] = y
x = y
if n!=nmax:
web[2*n, 0] = x
web[2*n, 1] = y
print(time.time()-a, "[sec.]")
mpmath.nprint(traj[-30:])
$ python baker_mp1.py
0.355421781539917 [sec.]
[0.170384, 0.340767, 0.681535, 0.36307, 0.72614, 0.452279, 0.904559, 0.809118, 0.618235, 0.236471, 0.472941, 0.945882, 0.891765, 0.78353, 0.56706, 0.13412, 0.26824, 0.536479, 0.0729585, 0.145917, 0.291834, 0.583668, 0.167335, 0.334671, 0.669341, 0.338683, 0.677365, 0.35473, 0.70946, 0.418921]
次にtrajをnumpy.arrayで覆ってみる
traj = np.array([mpmath.mpf("0")]*(nmax+1))
dtypeはobjectになる.出力は一度リストに戻さないと全桁出力される.
mpmath.nprint(traj[-30:].tolist())
実行結果はほとんど変わらないようだ.
$ python baker_mp2.py
0.36023831367492676 [sec.]
[0.170384, 0.340767, 0.681535, 0.36307, 0.72614, 0.452279, 0.904559, 0.809118, 0.618235, 0.236471, 0.472941, 0.945882, 0.891765, 0.78353, 0.56706, 0.13412, 0.26824, 0.536479, 0.0729585, 0.145917, 0.291834, 0.583668, 0.167335, 0.334671, 0.669341, 0.338683, 0.677365, 0.35473, 0.70946, 0.418921]
次にはややこしいのだが,listのなかにnumpy.arrayを入れ込む.
web = [np.array([mpmath.mpf(0)]*2*(nmax+1)),
np.array([mpmath.mpf(0)]*2*(nmax+1))]
traj = np.array([mpmath.mpf(0)]*(nmax+1))
traj[0] = x
a = time.time()
for n in range(1,nmax+1):
y = B(x)
web[0][2*n - 1] = x
web[1][2*n - 1] = y
traj[n] = y
x = y
if n != nmax:
web[0][2*n] = x
web[1][2*n] = y
print(time.time()-a, "[sec.]")
mpmath.nprint(traj[-30:].tolist())
実行結果は若干早くなった.
$ python baker_mp3.py
0.2923922538757324 [sec.]
[0.170384, 0.340767, 0.681535, 0.36307, 0.72614, 0.452279, 0.904559, 0.809118, 0.618235, 0.236471, 0.472941, 0.945882, 0.891765, 0.78353, 0.56706, 0.13412, 0.26824, 0.536479, 0.0729585, 0.145917, 0.291834, 0.583668, 0.167335, 0.334671, 0.669341, 0.338683, 0.677365, 0.35473, 0.70946, 0.418921]
numpy.arrayで
web = np.zeros((2*nmax+1,2),dtype="object")
web[0,0] = x
web[0,1] = 0
traj = np.zeros(nmax+1, dtype="object")
traj[0] = x
a = time.time()
for n in range(1,nmax+1):
y = B(x)
web[2*n - 1, 0] = x
web[2*n - 1, 1] = y
traj[n] = y
x = y
if n!=nmax:
web[2*n, 0] = x
web[2*n, 1] = y
print(time.time()-a, "[sec.]")
mpmath.nprint(traj[-30:].tolist())
としてもほとんど変わらない.
$ python baker_mp4.py
0.2934293746948242 [sec.]
[0.170384, 0.340767, 0.681535, 0.36307, 0.72614, 0.452279, 0.904559, 0.809118, 0.618235, 0.236471, 0.472941, 0.945882, 0.891765, 0.78353, 0.56706, 0.13412, 0.26824, 0.536479, 0.0729585, 0.145917, 0.291834, 0.583668, 0.167335, 0.334671, 0.669341, 0.338683, 0.677365, 0.35473, 0.70946, 0.418921]
データを倍精度で保存する.
web = np.zeros((2*nmax+1,2),dtype=np.float)
web[0,0] = float(x)
web[0,1] = 0
traj = np.zeros(nmax+1, dtype=np.float)
traj[0] = float(x)
a = time.time()
for n in range(1,nmax+1):
y = B(x)
web[2*n - 1, 0] = float(x)
web[2*n - 1, 1] = float(y)
traj[n] = float(y)
x = y
if n!=nmax:
web[2*n, 0] = float(x)
web[2*n, 1] = float(y)
print(time.time()-a, "[sec.]")
print(traj[-30:])
これもほとんど速度に変化なし.
$ python baker_mp5.py
0.3071897029876709 [sec.]
[0.17038373 0.34076746 0.68153493 0.36306985 0.72613971 0.45227941
0.90455883 0.80911766 0.61823531 0.23647062 0.47294124 0.94588249
0.89176498 0.78352995 0.5670599 0.13411981 0.26823961 0.53647923
0.07295846 0.14591691 0.29183383 0.58366766 0.16733532 0.33467064
0.66934128 0.33868256 0.67736512 0.35473024 0.70946048 0.41892095]
結論
いろいろ実装の方法を試してみたが,pythonでは基本的にappendを使わなければ速度的には変化ないという結論.
今回は一つの初期条件のみ対象としたが,統計量を計算する際には初期条件のサンプリングが必要となる.
その場合もやるべきだが,今回はここで力尽きる.
参考
- mpmath
- Julia:BigFloats and BigInts
- Mathematicaの内部実装について(数値および関連関数)
- カオス力学系入門 第二版 原著者:Robert L. Devaney (訳者:後藤憲一, 新訂版訳者: 國分寛司, 石井豊, 新居俊作, 木坂正史) 共立出版