目的
任意精度演算で対角化を実行してくれるmpmath(python)とMathematicaを使って,対角化に要する時間を計測したので備忘録として残す.
評価方法
評価した行列は一次元ハミルトニアン
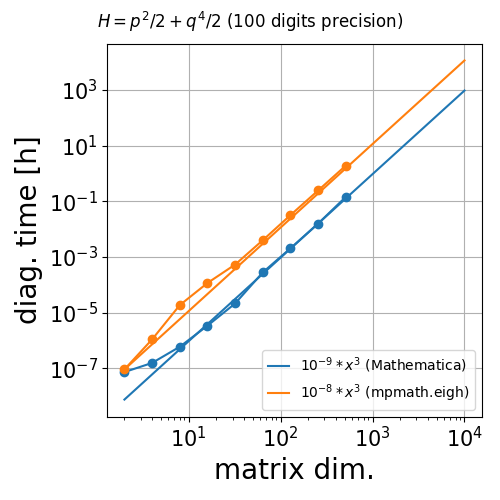
$$ H = p^2/2 + q^4/2 $$
を調和振動子の基底で構成したHermite 行列.
行列要素は100桁の精度で構成.対角化ルーティンは
- mpmath の eigh
- Mathematica と Eigensystem
を利用.
結果
Mathematica の方が約10倍程度早い.
課題
多次元では$10^4\times10^4$程度の行列を評価することになるのでmathematicaだと40日かかる.
lapackを多倍長拡張したmpackを使ってみたい.
追記
mpackをinstallして数時間だけ触ってみた.
ついでに速度を評価したので,追記として記録する.
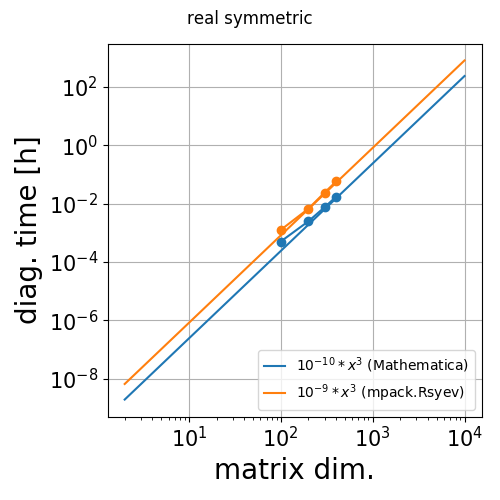
対角化した行列は対称実行列で
$a_{i,i}=i$, $a_{i+1,j}=i$, $a_{i,j+1}=i$ それ以外は0の要素を持つ実対称行列を使う.
mathematica とmpackのRsyevのルーチンを比較.
結果としてmpackはmathematicaより10倍程度早そう.
エルミートの場合はまだ評価していないが,Mathematicaより10倍程度早くなるのであれば$10^4\times 10^4$の対角化が4日で終わる計算になる.
これは非常に期待せざるを得ない.
しかし,まずはmpackを使えるようにならなければ.