はじめに
今回は、Amazon Braketを使って代表的な量子アルゴリズムを幾つか実装してみることにしました。量子アルゴリズムを学んでも、それが正しいことを机上の計算で確かめるだけでは、それが実際の量子デバイス上でワークするかどうか実感がわきません。その点、Amazon Braketでは後述するようにRegetti、IonQ、D-waveなど複数の量子コンピュータへのアクセスが可能です。同じアルゴリズムを異なるNISQな量子デバイスで計算することによって、リアルに量子アルゴリズムの正しさを実感できるのは魅力的です。
この記事では、量子アルゴリズムとして有名なDeutsch-JozsaのアルゴリズムとShorのアルゴリズムを取り上げます。後者はRSA暗号を解読できるアルゴリズムとして有名です。この記事が、量子コンピューティングを体験するきっかけとなれば幸いです。
Amazon Braket について
Amazon Braket は AWS が提供している量子コンピューティングサービスです。量子回路の設計を行い、ローカルシミュレーターまたはクラウドベースのマネージドシミュレーター SV1 で回路を実行できます。さらにこれらの古典シミュレータで設計された回路を、量子マシンで実行するような操作を Python の SDK を通して行うことができます。今回はこの Amazon Braket を活用して、量子アルゴリズムを構築、実行してみたいと思います。本記事は Braket が提供している Jupyter notebook 形式の環境にて実行した内容をご紹介しています。この環境へは Braket SDK がすでにインストールされていますので、すぐに始めることができます。回路の構築については、Braket ではいくつかの量子ゲート操作を提供しており、組み合わせて回路を構築します。追加できるゲートを確認してみましょう。
import string
from braket.circuits import Gate
gate_set = [attr for attr in dir(Gate) if attr[0] in string.ascii_uppercase]
print('Gate set supported by SDK:\n', gate_set)
出力結果は下記のようになります。なんとなく、馴染みのあるゲート操作が出力されているのではないでしょうか。
Gate set supported by SDK:
['CCNot', 'CNot', 'CPhaseShift', 'CPhaseShift00', 'CPhaseShift01', 'CPhaseShift10', 'CSwap', 'CY', 'CZ', 'H', 'I', 'ISwap', 'PSwap', 'PhaseShift', 'Rx', 'Ry', 'Rz', 'S', 'Si', 'Swap', 'T', 'Ti', 'Unitary', 'V', 'Vi', 'X', 'XX', 'XY', 'Y', 'YY', 'Z', 'ZZ']
回路の作成は、空の回路を作成し、ゲートを追加して構築していきます。試しにベル状態を構築してみました。
# ベル状態の回路を構築
bell = Circuit().h(0).cnot(0, 1)
print(bell)
T : |0|1|
q0 : -H-C-
|
q1 : ---X-
T : |0|1|
Deutsch-Jozsa のアルゴリズム
Deutsh-Jozsa のアルゴリズムは、古典アルゴリズムよりも、実行時間が短くなるとされる量子アルゴリズムの中で、一番最初に発見されたものの一つです。与えられた関数のオラクルの判定に使います。解くべき問題のサイズ $n$ に対し、古典アルゴリズムでは指数関数的に処理時間が増えるような問題に対して、量子計算を活用すると、多項式時間で収まることを示しました。
Braket を使った実装
例えば、$n=2$ とした $f_1(x_1, x_2)=x_1$ のような関数は $x_2$ の値によらず、$x_1$ の入力がそのまま出力されます。$x_1$ が 0 になるか 1 になるかは半々なので、この関数は均等なオラクルと言えます。オラクルの量子回路のイメージは下図のようになります。

オラクルは関数 $f$ の引数となる $2$ 量子ビットと制御ビットに対するユニタリ変換 $U_f$ として定義されます。オラクルで判定を行う際には、入力される量子ビットにそれぞれアダマール変換を行って重ね合わせ状態にした上でオラクルに入力します。オラクルの出力を再びアダマール変換した結果、制御ビット以外の出力が $\left|00\right>$ ならば、関数 $f$ は一定であり、それ以外の $\left|10\right>$, $\left|01\right>$, $\left|11\right>$ の何れかであれば、関数 $f$ は均等と判定できます。
それでは、均等な関数 $f_1(x_1,x_2) = x_1$ について、実際に量子回路を設計し、測定してみましょう。まずは、回路の設計は下記のようになります。
my_circuit1 = Circuit()\
.x(target=2)\
.h(range(3))\
.cnot(control=0, target=2)\
.h(range(3))
print(my_circuit1)
このように表記されました。
T : |0|1|2|3|
q0 : -H---C-H-
|
q1 : -H-H-|---
|
q2 : -X-H-X-H-
T : |0|1|2|3|
続いて、この回路を使った量子計算の実行です。今回はシミュレータである SV1 を活用しています。
device = AwsDevice("arn:aws:braket:::device/quantum-simulator/amazon/sv1")
my_bucket = f"amazon-braket-Your-Bucket-Name"
my_prefix = "simulation-output" # the name of the folder in the bucket
s3_folder = (my_bucket, my_prefix)
# タスクの定義と実行
task = device.run(my_circuit1, s3_folder,
poll_timeout_seconds = 100,
shots=1000)
result = task.result()
counts = result.measurement_counts
plt.bar(counts.keys(), counts.values());
plt.xlabel('bitstrings');
plt.ylabel('counts');
Deutsch-Jozsaのアルゴリズムでは、関数$f(x_1,x_2)$が一定な関数の場合、必ず$\left|00\right>$を返します。今回は$\left|10\right>$が返ってきていることが観測され、関数が均等なオラクルだと判定されます。
Shorのアルゴリズム
素因数分解を少ない計算量で解く、という量子計算では非常に有名なアルゴリズムです。
ここでは簡単な例についてBraketを使った実装を行います。
以下、簡単にアルゴリズムについて説明を行いますが、こちらについてはIBMQのShor's algorithmと次の教科書を参考にさせていただきました。
周期発見問題
周期発見問題と呼ばれる問題が解ければ、因数分解が効率的に行えることは1970年代から数学者の間で知られていました。周期発見問題は次のように定義されています。
2つの整数 $N, a$ が与えられたとき、 $a^r -1$ が $N$ の倍数となるような最小の整数 $r>0$ を求める
$r$ は $N$ を法としたときの $a$ の周期と呼ばれます。合同式を使うと、周期 $r$ は $a^r \equiv 1 (\mbox{mod} N)$ を満たします。量子計算によって、この周期 $r$ を少ない計算量で求めることができる、というのが利点となります。
素因数分解問題
素因数分解問題はその名の通り自然数 $N$ に対し、 $N=pq$ を満たす素数の組 $(p,q)$ を求める問題です。$N$ が大きくなるにつれて、この問題を解くための計算量が爆発的に増える、というのは有名な話だと思います。
詳細は何も説明しないので恐縮ですが、 $N$ と互いに素な整数 $x$ について $x^r \equiv 1~ (\mbox{mod}~ N)$ を満たす最小の $r$ を求めることができれば、古典アルゴリズムでも素因数分解問題を効率よく解けることが知られています。これはまさに $x$ の $N$ を法とした周期を求める問題です。
Shorのアルゴリズム
周期発見問題の部分を量子計算に行わせて、残りは古典計算で素因数をみつける、というのが Shorのアルゴリズムになります(以下の手順は量子情報科学入門3章からの引用です)。
- $x\in { 1,\ldots,N-1 }$ を一様ランダムに選ぶ
- 最大公約数 GCD($x,N$) を計算する。その値が $1$ でなければ GCD($x,N$) を出力して終了する
- $x^r \equiv 1~ \mbox{mod}~ N$ となる最小の $r$ を求める (量子計算部分)
- $r$ が偶数かつ $x^{r/2}\not\equiv -1 ~ \mbox{mod}~ N$ ならば、GCD($x^{r/2}+1,N$) と GCD($x^{r/2}-1,N$) が $N$ を割り切るか検査し、割り切るならそれを出力して終了する。そうでなければ最初の工程からやり直す
Braketでの実装
Shorのアルゴリズムと言っていますが、量子計算部分は周期発見問題なので、簡単な周期発見問題に対応する回路を組んでみようと思います。例として、IBMQのページと同様に $N=15, a=7$ を扱ってみます。このとき
7^2 \equiv 4,~ 7^3 \equiv 13,~ 7^4 \equiv 1 ~ (\mbox{mod} 15)
なので、周期 $r=4$ となります。
この問題を量子回路で表現する際に、 modular multiplication function $f(x)$ と呼ばれる関数を考えます。今の例では、具体的には $f(x)=7x~ (\mbox{mod} 15)$ です。この関数をユニタリー演算子 $U_f$ で表現し、これを回路で実現する、というのが目標になります。
ビット列で15を法とした整数を表現したベクトルを $\left|x\right>$ とすると、$U_f$ の作用は
U_f : \left|x\right> ~ \rightarrow ~ \left|7x~ (\mbox{mod} 15)\right>
なので、具体的に $\left|1\right>$ に作用させてみると
\left|1\right> ~ \rightarrow ~ \left|7\right> ~ \rightarrow ~ \left|4\right> ~ \rightarrow ~ \left|13\right> ~ \rightarrow ~ \left|1\right>
となり、$(U_f)^4$ で元の状態に戻っています。
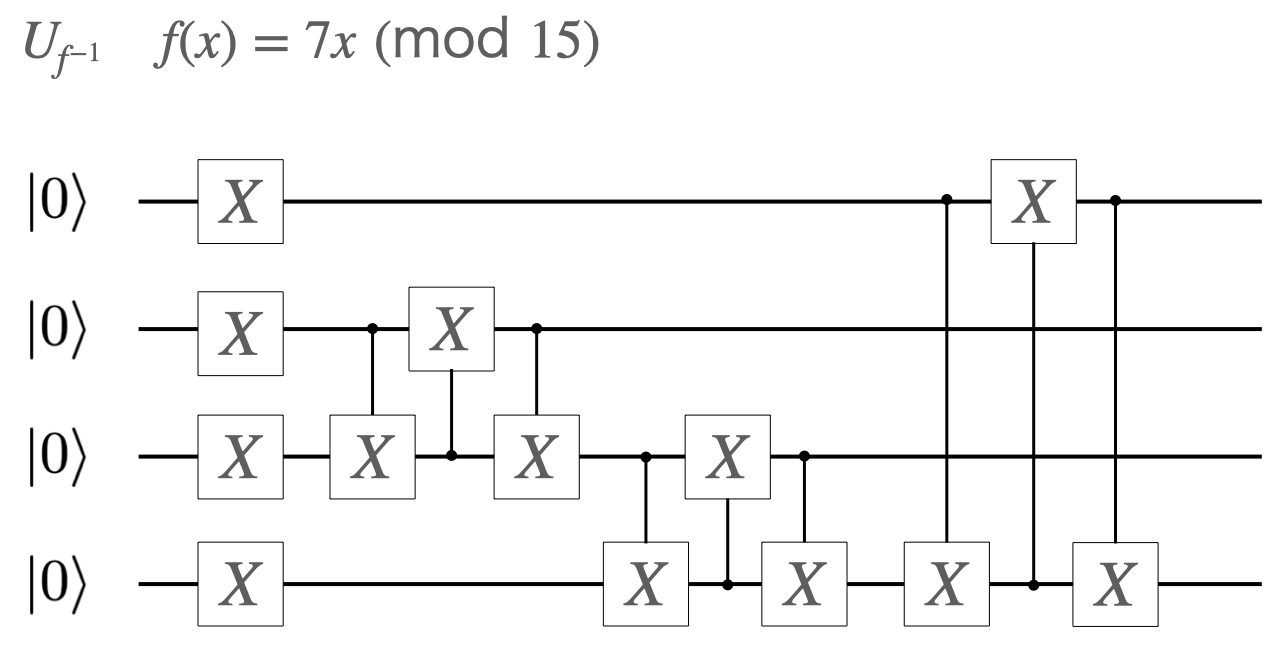
$U_f$ の量子回路における実装は次の形になります[Markov, Saeedi]。
アルゴリズムの関係上、これは $f^{-1}$ に対応するものになっていて、上で見せたものと逆向きに変換されます(なので本当は$U_{f^{-1}}$の回路です)。
また、各整数に対応する状態は次のようになります。Braketでは $\left|q_0q_1q_2q_3\right>$ という順で状態が表記されるようです。
| $x$ | 状態 |
|---|---|
| $1$ | $1000$ |
| $7$ | $1110$ |
| $4$ | $0010$ |
| $13$ | $1011$ |
前準備
やっと本題ですが、$7\times 1 ~(\mbox{mod} 15)$の回路をBraketで実装したコードは次のようになります。ほとんどチュートリアルとして用意されているノート(/Braket examples/getting_started/以下にあります)のコピペで実装できます。
# general imports
import matplotlib.pyplot as plt
# magic word for producing visualizations in notebook
%matplotlib inline
import string
import time
import numpy as np
# AWS imports: Import Braket SDK modules
from braket.circuits import Circuit, Gate, Instruction, circuit, Observable
from braket.devices import LocalSimulator
from braket.aws import AwsDevice, AwsQuantumTask
量子コンピュータの実機や、SV1と呼ばれるシミュレーターを使うためには、S3のbucketを指定して上げる必要があります。
# Please enter the S3 bucket you created during onboarding in the code below
my_bucket = "amazon-braket-Your-Bucket-Name" # the name of the bucket
my_prefix = "Your-Folder-Name" # the name of the folder in the bucket
s3_folder = (my_bucket, my_prefix)
# set up device
device = LocalSimulator()
device_sv1 = AwsDevice("arn:aws:braket:::device/quantum-simulator/amazon/sv1")
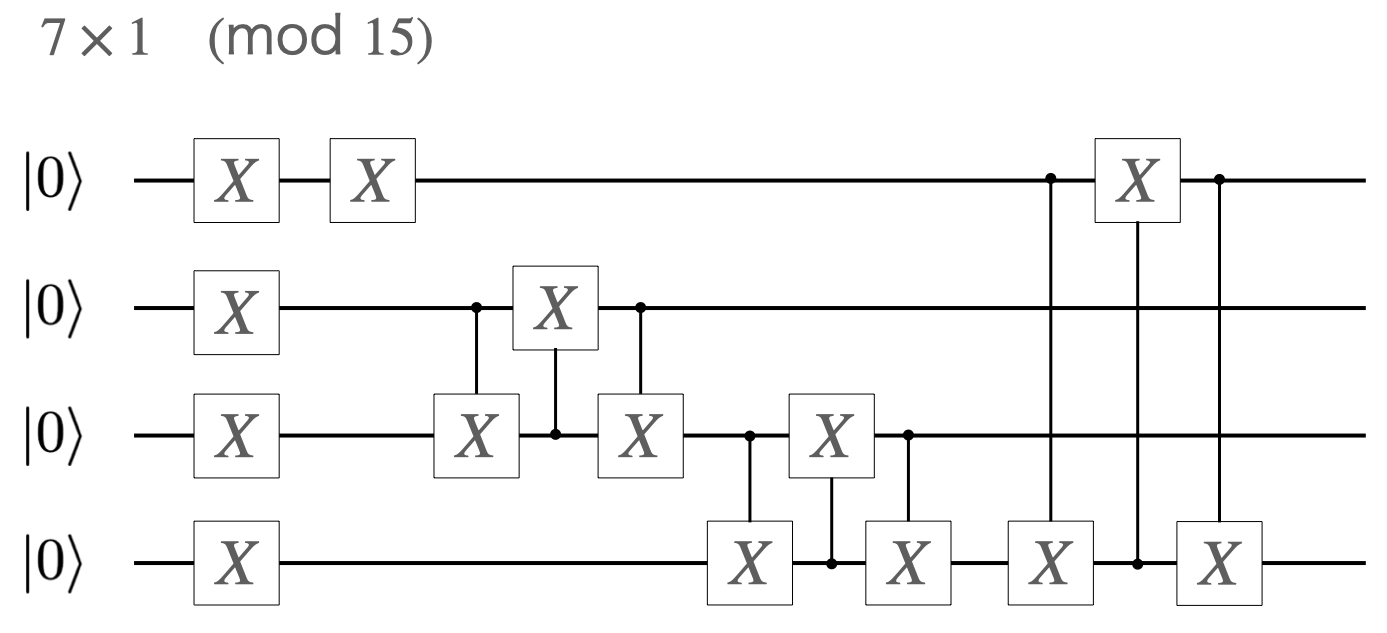
7×1 (mod 15)
回路図としては、まず1に対応する状態$\left|1000\right>$を$X$演算子で作成し、それに$U_{f^{-1}}$の回路をかけるものになります。
# Multi 7 \times 1 Mod 15
circ = Circuit()
# circ.x([0,1,2,3])
circ.x([0,1,2,3])
circ.x(0)
circ.cnot(control=1, target=2)
circ.cnot(control=2, target=1)
circ.cnot(control=1, target=2)
circ.cnot(control=0, target=1)
circ.cnot(control=1, target=0)
circ.cnot(control=0, target=1)
circ.cnot(control=0, target=3)
circ.cnot(control=3, target=0)
circ.cnot(control=0, target=3)
print(circ)
print(circ) とすることで組んだ回路の模式図を出してくれます。
T : |0|1|2|3|4|5|6|7|8|9|
q0 : -X-X-----C-X-C-C-X-C-
| | | | | |
q1 : -X-C-X-C-X-C-X-|-|-|-
| | | | | |
q2 : -X-X-C-X-------|-|-|-
| | |
q3 : -X-------------X-C-X-
T : |0|1|2|3|4|5|6|7|8|9|
ローカルシミュレーター
ローカルシミュレーターを使って、100回測定を実行してみます。
# run circuit
result = device.run(circ, shots=100).result()
# get measurement shots
counts = result.measurement_counts
# print counts
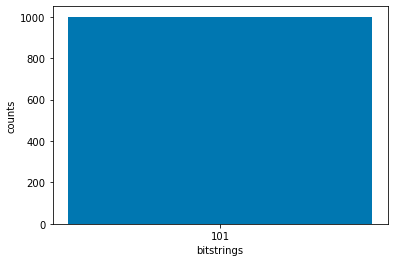
print(counts) # Counter({'1011': 100})
# plot using Counter
plt.bar(counts.keys(), counts.values());
plt.xlabel('bitstrings');
plt.ylabel('counts');
結果は100回とも$\left|1011\right> = \left|13\right>$となりました。$U_f\left|13\right>=\left|1\right>$なので正しいのですが、1つの状態だけが観測されるので少し面白みに欠けます。
SV1
では、SV1シミュレーターを使って同じことをやると次のようなコードになります。run の引数が少し違うだけでほぼ同じです。
# run circuit on SV1
result_sv1 = device_sv1.run(circ, s3_folder, shots=100, poll_timeout_seconds=24*60*60).result()
counts_sv1 = result_sv1.measurement_counts
print(counts_sv1) # Counter({'1011': 100})
# plot using Counter
plt.bar(counts_sv1.keys(), counts_sv1.values());
plt.xlabel('bitstrings');
plt.ylabel('counts');
そして結果も全く同じとなりました。もう少し実機のような結果(他の状態も観測される)を期待したのですが、100回程度ではあんまりぶれないのでしょうか?ちなみに実機ほどではないですがSV1を使うとBraketで立てているSagemakerインスタンスとは別に料金が発生します。
IonQ
では、実機を回してみます。今回はシミュレーターとほぼ同じ書き方で実行が可能なIonQで試してみました。
# set up device
ionq = AwsDevice("arn:aws:braket:::device/qpu/ionq/ionQdevice")
# run circuit with a polling time of 2 days
ionq_task = ionq.run(circ, s3_folder, shots=100, poll_timeout_seconds=2*24*60*60)
# get id and status of submitted task
ionq_task_id = ionq_task.id
ionq_status = ionq_task.state()
# print('ID of task:', ionq_task_id)
print('Status of task:', ionq_status)
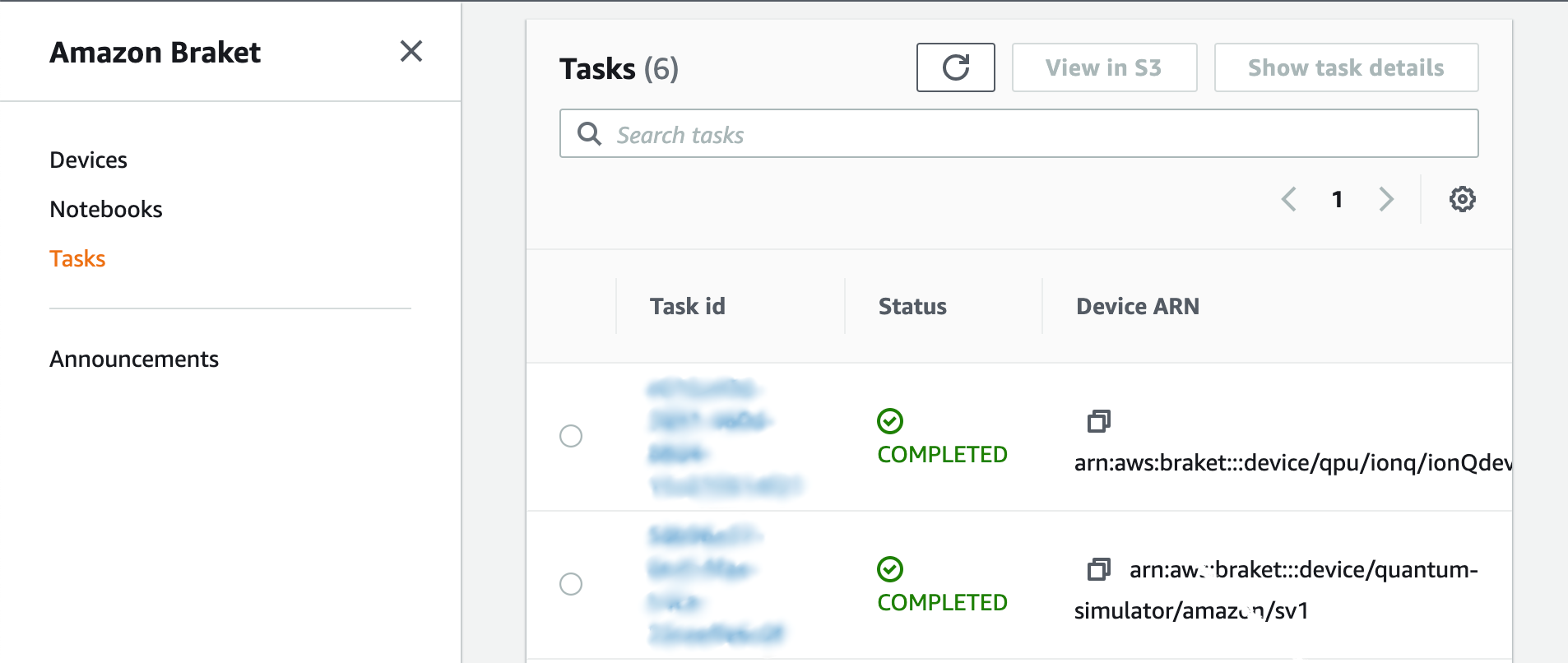
IonQとRigettiは実機が利用できる時間が限られているため、上記を実行すると Status of task: CREATED とタスクが生成され、実機が動いてくれるまで待ちになります。自分が投げたタスク一覧は、Braketの Task というタブから確認可能です。
タスクが完了したら、タスク一覧で COMPLETED と表示され、タスク詳細にARNと呼ばれる実行結果に対応するラベルが発行されています。
ARNを使って、実行結果を確認することが可能です。
# recover task
task_load = AwsQuantumTask(arn=ionq_task_id) # Task details からコピーしたARNを使う
# print status
status = task_load.state()
print('Status of (reconstructed) task:', status)
# terminal_states = ['COMPLETED', 'FAILED', 'CANCELLED']
# get results
results = task_load.result()
# get all metadata of submitted task
metadata = task_load.metadata()
# example for metadata
shots = metadata['shots']
machine = metadata['deviceArn']
# print example metadata
print("{} shots taken on machine {}.".format(shots, machine))
# get measurement counts
counts = results.measurement_counts
print('Measurement counts:', counts)
# plot results: see effects of noise
plt.bar(counts.keys(), counts.values());
plt.xlabel('bitstrings');
plt.ylabel('counts');
plt.tight_layout();
plt.savefig('bell_ionq.png', dpi=700);
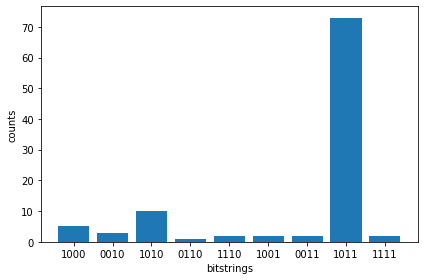
今回実行した結果は以下の通りです。
# print結果
Status of (reconstructed) task: COMPLETED
100 shots taken on machine arn:aws:braket:::device/qpu/ionq/ionQdevice.
Measurement counts: Counter({'1011': 73, '1010': 10, '1000': 5, '0010': 3, '1110': 2, '1001': 2, '0011': 2, '1111': 2, '0110': 1})
ピークは$\left|1011\right>$ですが、他の状態も観測されていることがわかります。
Shorのアルゴリズム、というセクションですが、周期発見問題に関係する回路1つを Amazon Braket 使ってやってみた、というところで終わりです。ここでは$\left|1\right>$に対応する入力を行いましたが、$X$演算子を使って2進数表示させた$0\sim 15$の整数値を作れば他の値でも実行可能です。
最後に
Amazon Braket が出てきたことで、AWSのアカウントがあればすぐに量子コンピュータの実機が動かせるようになったのは感動的でした。実機の値段がわからず恐る恐る回したのですが、IonQでは100ショット1USDでしたので、思ったよりも金額が掛からなかったのも良かったです。
ブレインパッドでは、量子コンピュータに興味がある人が集まって勉強会を行っています。BrainPad Advent Calendar 2020 1日目のohtamanさんの記事でも Amazon Braket で D-Wave を使っていたようです。実機が触れることでチャレンジできることの幅が広がったので、これからも色々試してみたいと思っています。