ChatGPTと地図描画ライブラリでつくる地図

　大学時代の友人たちと定期的に開催している"各々興味のあること"を調べて発表する『第４回　誰も知らなさそうなこと学会』で発表した内容をまとめておく。

1. イントロダクション

1-1. 地図を作りたい

　多くの人にとって地図は検索対象であり、旅先の情報/目的地への経路/地形や標高といった情報を調べるものだが、人によっては”地図を作りたい”という時もあるのではないだろうか。
   （例）
     ・訪問先/移動経路の記録をしたい
     ・Blog/Vlogに地図を載せたい
     ・自分で作成した経路を伝えたい　ほか

　今回、こうした「自分で地図を作りたい」という希望をGoogle Colaboratory上で実現するコード（スクリプト）をいくつか掲載する。

2. 地図描画ライブラリ

2-1. OpenStreetMap / Leaflet / Folium

　今回使用する地図描画ライブラリ/WEBサービスは主に三つ。

2-1-1. OpenStreetMap

・ユーザーが無料でアクセスできるオープンソースの地図データベースおよび地図描画プロジェクト
・クレジットの明記により、データを自由にコピー/配布/送信/改変することが可能
・類似のサービスとして「Googleマップ」「地理院地図」が挙げられる

2-1-2. Leaflet

・対話型のオープンソース JavaScript 地図ライブラリ
・主要なデスクトップおよびモバイル プラットフォームで動作。拡張性◎

2-1-3. Folium

・Leaflet.jsをPythonライブラリ化したもの
・Pythonで簡易的にマップを用いてデータの可視化が可能
・類似のサービスとして「leafmap」

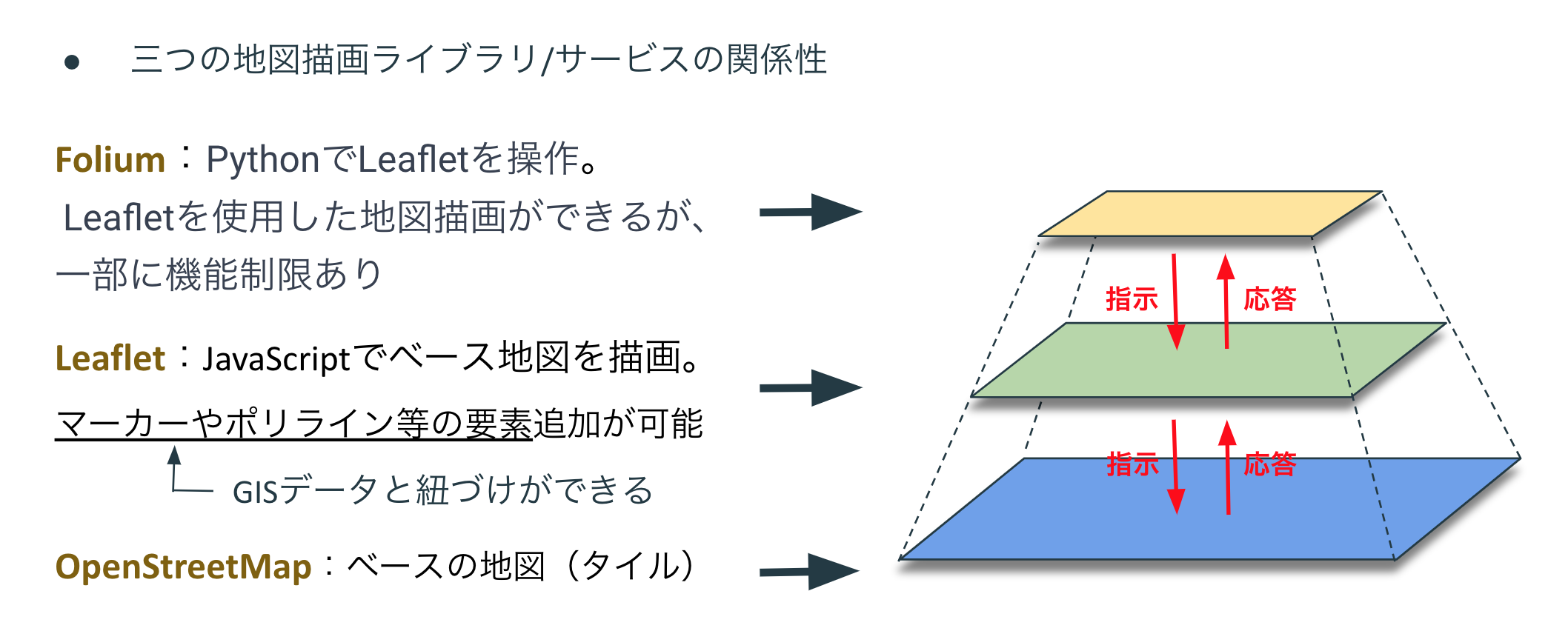
2-2. 三つの地図描画ライブラリ/サービスの関係性

　

　 2-1. で紹介した三つの地図描画ライブラリ/サービスの関係性を簡単にまとめたものが上図になる。
　まず最下層のベースの地図（タイル）として機能するのがOpenStreetMap。
　その上層でLeafletが動作し、JavaScriptでベース地図を描画する。この際、マーカーやポリライン等の要素追加が可能であり、これらの要素についてはGISデータと紐づけることもできる。
　最上層に位置するのがFolium。Foliumは、PythonでのLeaflet操作、地図描画を可能とするライブラリだが、その機能には一部に制限がある。

3. 私の体当たり型プログラミング勉強法

　記事の本題からは外れるが、ここで『私の体当たり型プログラミング勉強法』について記載する。
　私は普段非IT系の仕事をしており、学生時代も特段プログラミングを専攻したことはないため、プログラミングの知識はほとんど０といって差し支えない。
　知識の無い自分がコードを記述する際お世話になるのがChatGPTだ。
　

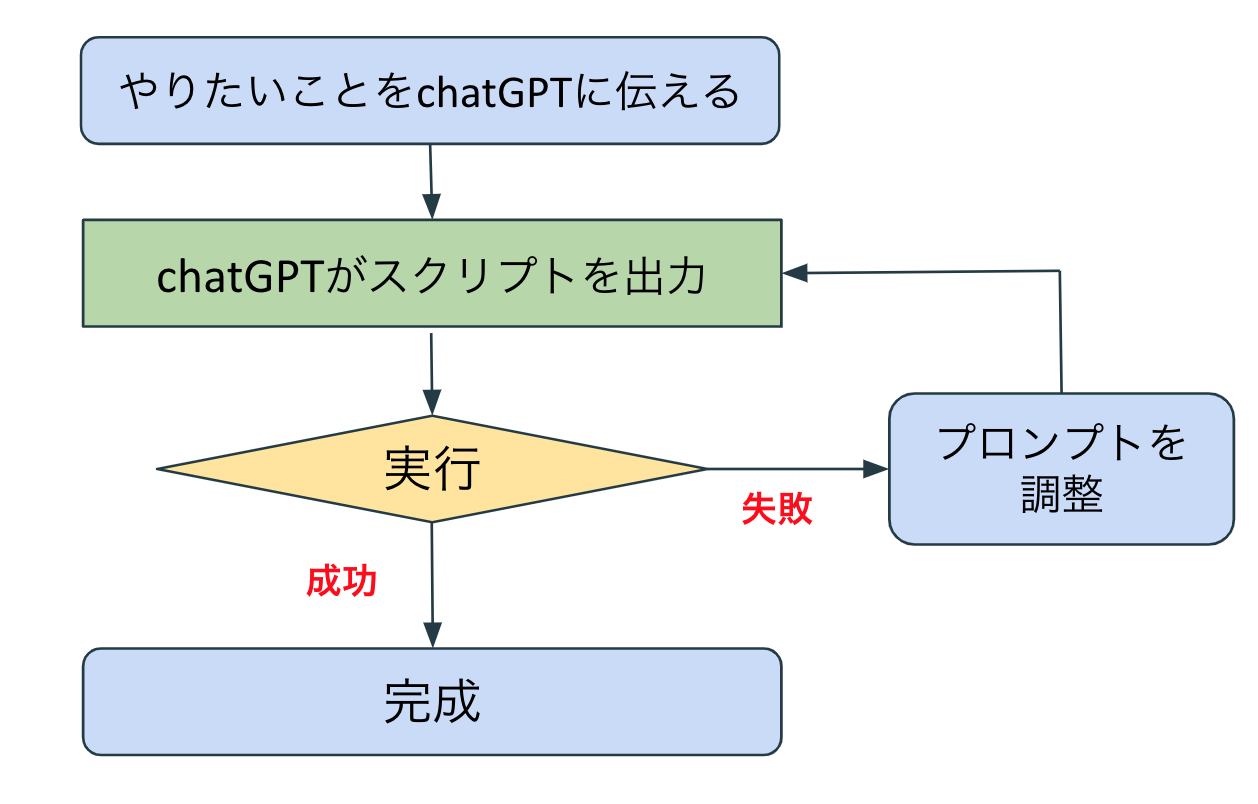
　上記が目的のスクリプトはChatGPTと協働して作成していく際のフローチャートである。
　基本的にはChatGPTに対して「○○をするコードを書いて」と指示し、その結果をGoogle Colaboratoryにコピペして実行、上手くいくまでChatGPTとのやり取りを繰り返す、という方針でコードを作成している。
　実行が失敗するときはエラー文をChatGPTのプロンプトに入力するだけで修正版のコードを再出力してくれる。非常に便利だ。

　今回の発表では、五つのスクリプトを作成、さらにその背景知識等もChatGPTで調べた結果、ChatGPTとのやり取り回数は軽く500回を超えた。

　ChatGPTとのやり取りでは、以下のことに気を付けた。

   ・抽象的な指示で望んだ回答を得られない場合、具体的な指示に切り換える。
      ...簡単な例を与える等が有効。
   ・ChatGPTから”未知の専門用語”を引き出し、その語句を梃子にして自力での調査やプロンプト入力を行う
      ...今回の地図描写コード作成では「球面三角法」や「ポリライン」といった語句がキーワードになった。
   ・５回出力に失敗したら、プロンプト作成の方針を変更する
      ...５回出力に失敗するときは、ChatGPTも指示者も袋小路に入り込んでいる可能性が高い。望ましい結果を得るためのアプローチ自体を考え直すのが得策。

4. 目標と成果品

　今回は以下の五つの地図描画スクリプトを作成した。

1-i.マップ上にピンを立てる

2-i.フライトマップ風の地図（静止画）

2-a.フライトマップ風の地図（マップアニメーション）

3-i.東海道新幹線のルートマップ（静止画）

3-a.東海道新幹線のルートマップ（マップアニメーション）

　記事を分けつつ、上記の五つのスクリプトを紹介する。

4-1-i.マップ上にピンを立てる

Googleマップでも、地理院地図でも、利用者の多くが使いたいと思うことが多いであろうこの機能（その割に直感的な操作ができないような印象がある）。

　以下がFoliumを用いてOSM上にマーカーを立てるスクリプト。

map_marker.py

import folium

# Dallasの緯度経度情報
dallas_lat = 32.7767
dallas_lon = -96.7970

# 地図を作成（tilesを指定）
m = folium.Map(location=[dallas_lat, dallas_lon], zoom_start=10)
# m = folium.Map(location=[dallas_lat, dallas_lon], zoom_start=10, tiles='Stamen Terrain')

# マーカーを追加（ポップアップに'Dallas, TX'と入れる）
folium.Marker([dallas_lat, dallas_lon], popup='Dallas, TX').add_to(m)

# 地図を表示
m

# 地図をHTMLファイルとして保存
# m.save("dallas_map.html")

gistはこちら → gist：map_marker.py

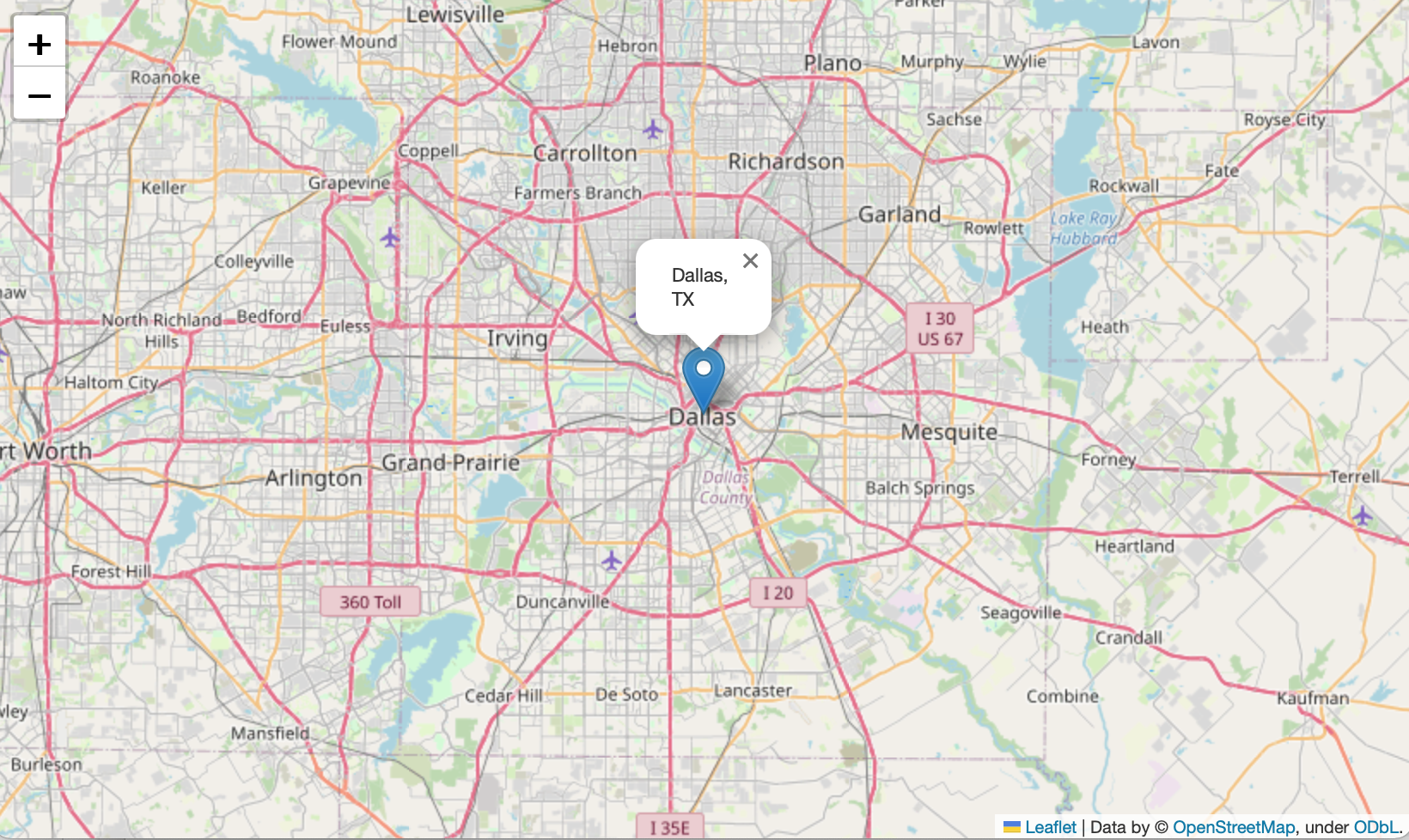
　実行結果のスクリーンショットは以下の通り。

　マーカーを立てる地点の緯度経度を指定すれば地図にマーカーを立てられる。
　マーカーにポップアップで語句を表示することもできる。

4-2-i. フライトマップ風の地図を描く

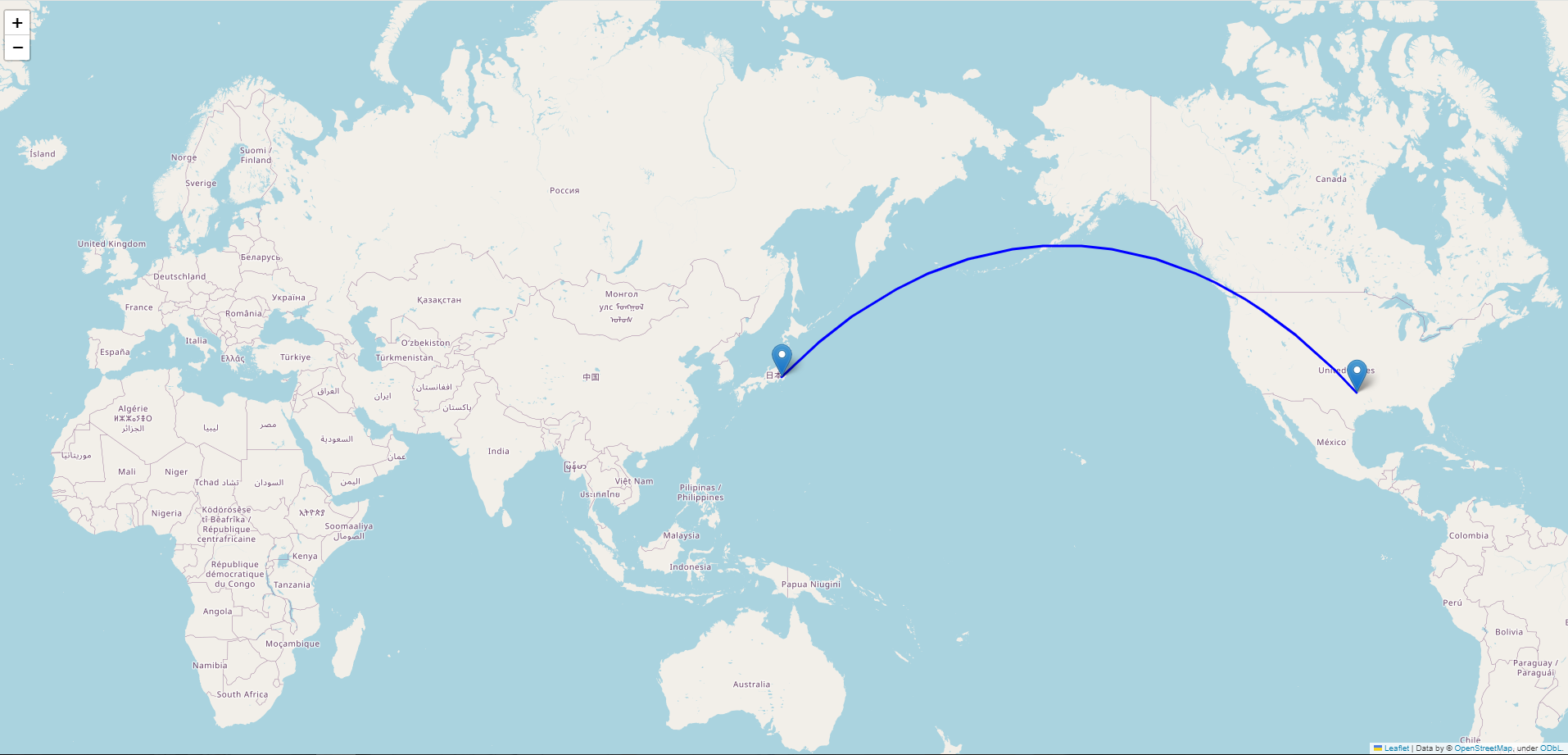
　フライトマップ風に“指定した２点間を地球が球体なことを考慮し最短経路で結ぶ”地図（静止画）を描くスクリプト。

　「Jetlovers」に着想を得て作成。実際の飛行ルートと一致する訳ではないことに留意。

map_flight.py

import folium
import numpy as np

#指定した２点間を球体である地球を考慮し最短経路で結ぶスクリプト（日付変更線を横切る）
# 球面三角法を使用して大円を計算する関数
def great_circle_points(point1, point2, num_points):
    lat1, lon1 = np.radians(point1)
    lat2, lon2 = np.radians(point2)

    # 球面三角法による角度（ラジアン）を計算
    angles = np.linspace(0, 1, num_points)
    distance = np.arccos(np.sin(lat1) * np.sin(lat2) + np.cos(lat1) * np.cos(lat2) * np.cos(lon2 - lon1)) # 球面三角法の余弦定理の式変形（２点と北極点の3点を結んだ球面三角形を考える）

    # 大円上の各点の緯度経度を計算
    points = []
    for angle in angles:
        x = np.sin((1 - angle) * distance) / np.sin(distance) * np.cos(lat1) * np.cos(lon1) + np.sin(angle * distance) / np.sin(distance) * np.cos(lat2) * np.cos(lon2)
        y = np.sin((1 - angle) * distance) / np.sin(distance) * np.cos(lat1) * np.sin(lon1) + np.sin(angle * distance) / np.sin(distance) * np.cos(lat2) * np.sin(lon2)
        z = np.sin((1 - angle) * distance) / np.sin(distance) * np.sin(lat1) + np.sin(angle * distance) / np.sin(distance) * np.sin(lat2)
        lat = np.arctan2(z, np.sqrt(x ** 2 + y ** 2))
        lon = np.arctan2(y, x)

        # 経路を180度の子午線を横切るように修正
        if lon - lon1 < -np.pi:
            lon += 2 * np.pi
        elif lon - lon1 > np.pi:
            lon -= 2 * np.pi

        points.append((np.degrees(lat), np.degrees(lon)))

    return points

# 羽田空港の緯度経度
haneda_lat = 35.5533  # haneda_lat = 33.4484（Phoenixの緯度）
haneda_lon = 139.7811 # haneda_lon = -112.0740（Phoenixの経度）
# Dallasの緯度経度
dallas_lat = 32.7767
dallas_lon = -96.7970

# 地図を作成
m = folium.Map(location=[haneda_lat, haneda_lon], zoom_start=3)

# 羽田空港にマーカーを追加
folium.Marker([haneda_lat, haneda_lon], popup='Haneda Airport, Tokyo').add_to(m)

# 大円上の点を計算
num_points = 100
great_circle = great_circle_points((haneda_lat, haneda_lon), (dallas_lat, dallas_lon), num_points)

# 大円を地図に追加
folium.PolyLine(locations=great_circle, color='blue').add_to(m)

# Dallasにマーカーを追加（修正後の位置に変更）
folium.Marker([great_circle[-1][0], great_circle[-1][1]], popup='Dallas, TX').add_to(m)

# 地図を表示
m

# 地図をHTMLファイルとして保存
# m.save("dallas_map.html")

　gistはこちら　→　gist：map_flight.py

　実行結果のスクリーンショットは以下の通り。

　スクリプトの肝は下記☟の「球面三角法の余弦定理」を用いた２点間の距離(弧の長さ)計算だろう。

　ここで求めた”distance”(２点間の距離)をもとに、中間点を指定個数算出、それらを結ぶことでルートマップを作成する。

「球面三角法の余弦定理」ほか、球体上の２点間の距離を求める計算法については、このページの解説が詳しい。→　Calculate distance, bearing and more between Latitude/Longitude points

4-3. つづく

　そのほかの成果については、別記事に譲る。

   2-a.フライトマップ風の地図（マップアニメーション）
　→ フライトマップ風の地図（マップアニメーション）をつくる

   3-i.東海道新幹線のルートマップ（静止画）
   3-a.東海道新幹線のルートマップ（マップアニメーション）
　→ 東海道新幹線のルートマップを描く

5. 参考文献

・「GISファイルフォーマットの簡単なまとめ/地図のワークブック」
・Leaflet
・Leafletの使い方（埼玉大学教育学部人文地理学　谷謙二研究室）
・OpenStreetMap Japan
・folium 0.15.1
・foliumの基本的な使い方とオープンデータ活用
・Wikipedia「球面三角法」
・球面三角法の簡潔かつ体系的な理解への試み（国土地理院）
・２地点の距離の導出
・Wikipedia「ラジアン」
・緯度、経度って何だろう？（国土地理院）
・Jetlovers
・Calculate distance, bearing and more between Latitude/Longitude points
・Wikipedia「ランベルト正積方位図法」
・chatGPT 3.5