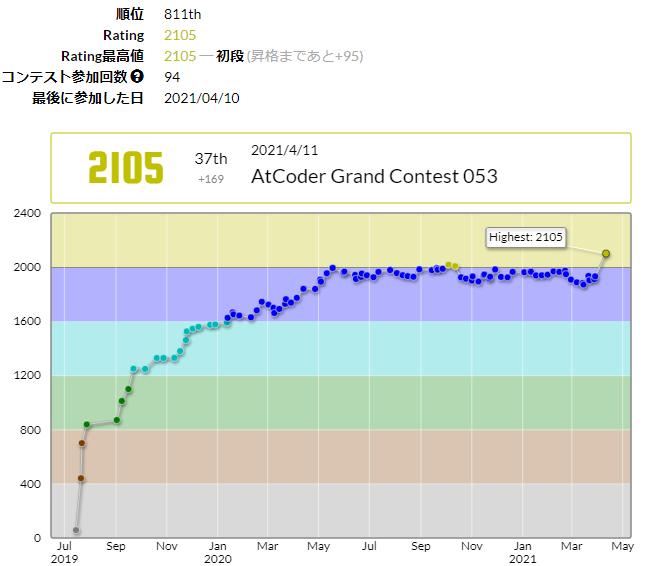
hamamuと申します。
AGC053で大成功して(再)入黄できたので(もう1か月たってしまいましたが)、色変記事として、黄色を目指してやってきたことを書きました。他の記事ではあまり見たことがない取り組みを選んで書いたので、お役に立つ部分があるかもしれません。特に「日本語コーディング」は意外と多くの人に役立つかも知れないと思っているので、ぜひぜひ読んで下さいませ!
自己紹介
自分の特徴を並べてみます。
- 中年である(1975年生まれ)
- 子供の頃からアルゴリズムが大好きだった、パズルも大好きだった
- 仕事は研究開発関連でプログラミングは日常、高速化も日常茶飯事
- かなり難しい問題でも時間をかければ結構解ける
- しかし解くのが遅い、特に実装が遅い
自分の年代では、競技プログラミングを知っている人がほとんどいません。参加者の中では相当高齢な方だと思います。レートに年齢をかけ算すると、一気に銀冠にジャンプアップします!(きりさん作成のレート×年齢ランキングより)
2年ほど前、たまたま仕事でヤマト運輸プログラミングコンテスト2019を知り、AtCoderを知りました。少し参加してみると、自分の好きなものが濃縮されている世界で、そのままどっぷりとはまってしまいました。アルゴリズムを考えるのも好き、プログラミング自体も好き、レーティングという数値を上げるためにコツコツ努力するのも好きで、ついでに仕事でもちょくちょく役立つし、会社には「週末は自己啓発に励んでいます」と意識高い系人間であるかのように言うことができるし、いいことだらけです。良い趣味を見つけることができて本当に良かったと思います。
自分は、かなり難しい問題でも時間をかければ解けることが多いのですが、解くのが遅い、特に実装が遅いです。
AtCoder Type Checker
https://atcoder-type-checker.herokuapp.com/
では多く解くタイプと判定されていました。

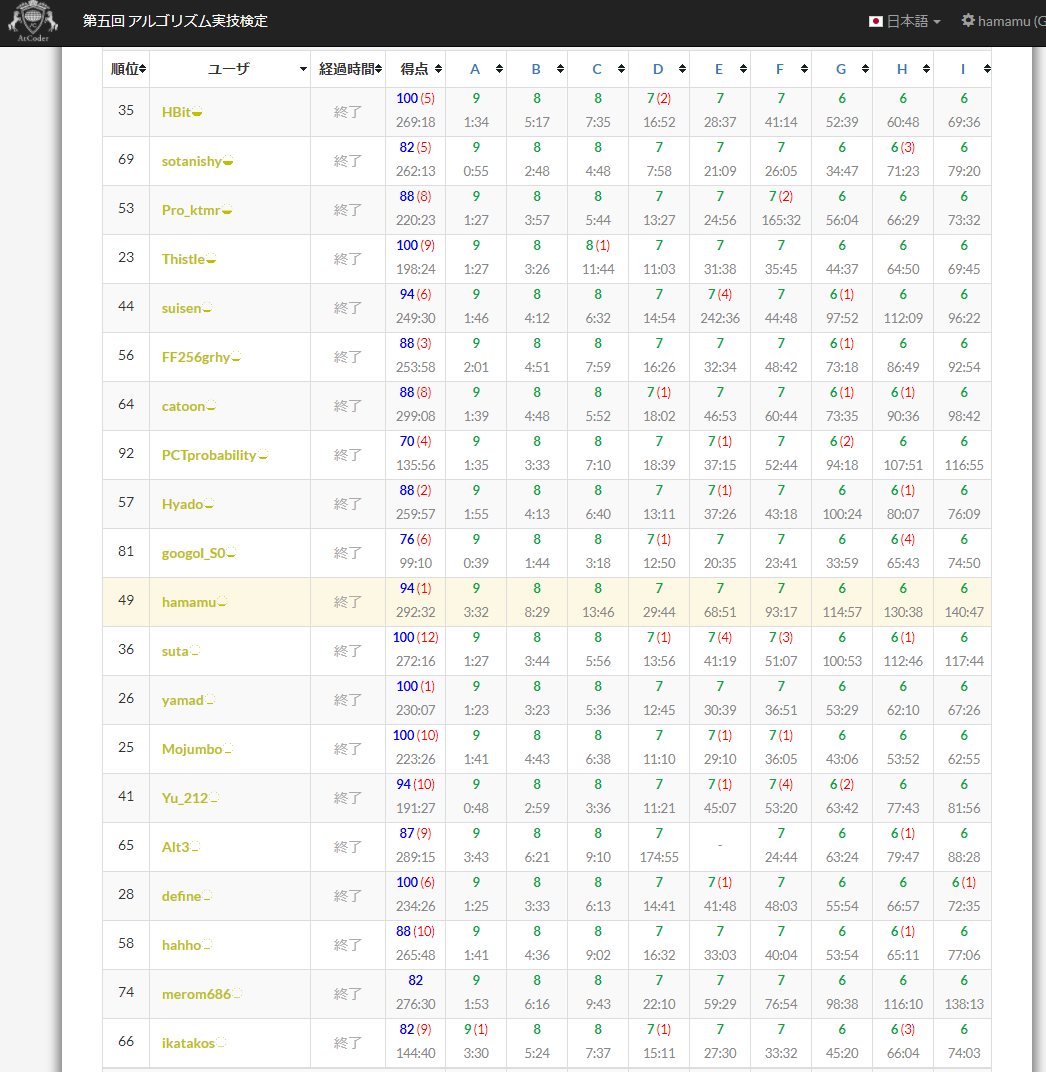
実装の遅さについては、実装力を試されるPASTで顕著に出ていました。以下はPAST5のバチャの序盤9問です。同レート帯の方々と比べると、概ね2倍ほどの差がついています…
では、以降、各種取り組みを書いていきます。
3種類の精進
精進を3種類に分類して、意識して取り組む時間を分けています。
- 実装精進
- 実装速度upにつながるあれこれ。**PCの前にいないとできない**。
- 勉強精進
- 新しいアルゴリズムなどの勉強。今はFPSを勉強中。**スマホを見られる環境ならできる**。電車内、バス内など。
- 考察精進
- 難しい問題の考察パートだけ考える精進。**何もなくてもできる**。風呂、寝る前、徒歩時など。
下に行くほどいつでもできる精進です。上の精進が足りないなら、上の精進ができる時間にうっかり下の精進をしないよう気を付けないといけません。自分は明らかに実装速度が課題なので、PCの前に座れるときは意識して実装精進をやるようにしています。
実装が遅い原因についての一考察
実装が遅い原因は、人によって何通りかの原因に分かれそうですが、自分の場合は短期記憶力が低いせいだと考えています。年齢とともに著しく落ちていくのを実感してます。子供の頃はやたら記憶力が良かったので、中学生の頃に競プロに出会っていたかった…
なぜ短期記憶が重要かというと、プログラミングではスタックに積んでいくような思考が多いから、です。後で説明しますが、スタックに積まれたものは順序が入れ替わっていて覚えにくいです。
例えば、こんな問題を解くことを考えてみましょう。
長さ $N$ の数列 $A=(A_0, A_1, \cdots, A_{N-1})$ と整数 $K$ が与えられる。$A$ の長さ $K$ の区間 $A_i, A_{i+1}, \cdots, A_{i+K-1}$ の、区間内最大値と区間内最小値の差を $d_i$ とする。$\min_i d_i$ は?($1 \le K \le N \le 10^5$)
いろいろな解き方がありそうですが、区間内の全ての値をmultisetに入れる方法を選んだとします。考察パートは、「multisetなら、区間を1つずらすのが $O(\log K)$、区間maxとminを得るのが $O(1)$、区間をずらす回数が $O(N)$ だから全体で $O(N\log K)$ 、よし解けるぞ」という感じでシンプルに終わります。
しかし、これをコードに落とすところで、頭のスタックにどんどん積まれていくと思うのです。はじめに頭の中にあるのはこんな感じ。
1 区間を左端から右端までずらしながら
2 区間max、minを得る
3 max-minの最小値を更新
1つ目の「区間を左端から右端までずらしながら」を考え始めると、その中で3つほど考えることがでてきました。脳内スタックに積まれます。
1-1 for文の範囲は?
1-2 あらかじめ先頭をmultisetに入れなきゃ
1-3 区間を1つずらすには?
1 区間を左端から右端までずらしながら
2 区間max、minを得る
3 max-minの最小値を更新
「1-1 for文の範囲は?」を紙に書いて考えます。区間の左端が $0$ から $N-K$ まで動くと分かります。for文をコードにし、脳内スタックから削除します。1-2も、先頭 $K$ 個をmultisetに入れるコードを書き、脳内スタックから削除します。1-3を考えようとします。またその中で3個ほどやること/考えることが出てきました。これもスタックに積まれます。
1-3-1 i=0の時はずらさないからfor文をi=1~にかえなきゃ
1-3-2 左端をmultisetから削除して
1-3-3 右端をmultisetに追加
1-3 区間を1つずらすには?
1 区間を左端から右端までずらしながら
2 区間max、minを得る
3 max-minの最小値を更新
1-3-1はすぐに片づけて、1-3-2を更に考えます。multisetから1つ削除するのは面倒で、findしてからeraseです。
1-3-2-1 findする
1-3-2-2 eraseする
1-3-2 左端をmultisetから削除して
1-3-3 右端をmultisetに追加
1-3 区間を1つずらすには?
1 区間を左端から右端までずらしながら
2 区間max、minを得る
3 max-minの最小値を更新
findの対象は?紙を見て考えて、$A_{i-1}$ です。
1-3-2-1-1 対象は$A_{i-1}$
1-3-2-1 findする
1-3-2-2 eraseする
1-3-2 左端をmultisetから削除して
1-3-3 右端をmultisetに追加
1-3 区間を1つずらすには?
1 区間を左端から右端までずらしながら
2 区間max、minを得る
3 max-minの最小値を更新
こんな感じで、スタックにどんどん積まれていくイメージです。ちょうど、dfsをスタックで実装した時の挙動です。
そして、このスタックの中身というものは、少なくとも私にはとても覚えにくいものです…。dfsでいうと、一度深い階層まで探索した後、浅い階層に戻ってきたときに、思い出すのが大変。同じ階層のものは、関連や順序があるので思い出しやすいのですが、浅い階層に戻る時は、自然な思考の流れではないので思い出しにくいのだろうなと思います。
また、深い階層で思考が発生すると、記憶がみるみる消えていきます。例えば、multisetからの削除に慣れていなくて、「確かeraseは、同じ値が全部消えちゃうんだよな、1つだけ消すにはどうやるんだっけ…?そうだ、find使ってイテレータを得て、それから…」などと思考してしまうと、脳内スタックが壊れていきます。
体感的には、スタックの深さを $D$ とすると、実装困難度は $O(D^2)$ くらいです。
…というのは冗談として、PCで例えるなら、 $D$ がある程度増えるとCPUのキャッシュに乗らなくなるということだと思います。キャッシュに乗っているうちは高速動作(高速実装)できるが、乗らなくなるとメモリやハードディスク(紙に書いたメモ)を見に行くため遅くなる。もしくは再計算が必要になる(再度処理の流れを考える)ので遅くなる。紙のメモ無しで全部再計算すると、本当に $O(D^2)$ かもしれません。キャッシュに乗っているうちは $O(1)$ で、乗らないと $O(D^2)$ 。
この脳内スタック短期記憶力そのものを鍛える(キャッシュ容量を増やす)のは、残念ながらほぼ無理なんだろうなと思います。そこで、何らかの工夫により、少しでも記憶量を減らしてキャッシュに乗るようにしたい、という取り組みが次節です。
実装精進:ライブラリ整備について
実装精進を思い立った当初は、簡単な問題を早解きしまくるのが良いかと思い、時間を測って解いたりしていました。これは、脳内スタック問題に対する効果の視点で言うと、
- 色々な処理を思考停止で書けるようになる → 脳内スタックが消えずに済む
- スタックを「積む」方向ではなく、同じ階層に「並べる」方向に思考できるようになる(典型的な処理を前から順に書けるようになるイメージ) → 階層が深くならない
という感じの効果がありそうです。しかしほどなく腱鞘炎が悪化して、タイピングしまくる練習ができなくなってしまいました…
その後は、1問解いたら、どうすればもっと速く実装できるかを徹底的に考えるようにしています。その結果出てくる対策として多いのは、ライブラリ整備です。多いというか、ライブラリ整備は時間がかかるので、結果的に普段の実装精進≒ライブラリ整備になっています。
ライブラリ整備とは言っても、目的は実装速度向上です。前節の考察をもとに、
短期記憶量を減らしたい!
スタックを浅くしたい!
余計な思考を減らしたい!
というモチベーションで整備しています。もちろん「このライブラリがあれば貼るだけになる」というタイプの普通のライブラリも作りますが、それだけでなくちょっと変わったタイプのものも作っています。以下、他の人があまり作ってなさそうなものをご紹介します。
set、multisetのラッパー
set、multisetの使い方になかなか慣れないので、なるべく自分が直感的に使えるようなインターフェースを作りました。いろいろ作ってますが、自分には以下にあげた6つのメンバ関数が超便利で、「スタックを浅くしたい」「余計な思考を減らしたい」に貢献しています。
-
erase1(x):xを1つ削除 -
contains(x):xがあればtrue -
front(),back():先頭/末尾を見る -
pop_front(),pop_back():先頭/末尾を削除
ちなみに、contains(x)というメンバ関数は、C++20では標準になるらしいです1。
setのラッパーのソース
template<class T> struct SET{
set<T> s;
typename set<T>::iterator it;
bool empty() const { return s.empty(); }
ll size() const { return (ll)s.size(); }
void clear() { return s.clear(); }
bool insert(const T &x){ bool r; tie(it,r)=s.insert(x); return r; }
template <class It> void insert(It b,It e){ s.insert(b,e); }
void erase(const T &x){ s.erase(x); }
void eraseit(){ s.erase(it); }
void swap(SET &b){ s.swap(b.s); }
bool contains(const T &x){ find(x); return it != s.end(); }
void find(const T &x){ it=s.find(x); }
T next() { return *(++it); }
T prev() { return *(--it); }
pair<T, bool> Next(){
if (it!=s.end()) it++;
if (it!=s.end()) return {*it,true};
else return {T(),false};
}
pair<T, bool> Prev(){
if (it!=s.begin()) return {*(--it), true};
else return {T(),false};
}
T front() const{ return *s.begin(); }
T back() const{ return *(--s.end()); }
void pop_front(){ s.erase(s.begin()); }
void pop_back(){ s.erase(--s.end()); }
void push_front(const T &x){ it=s.insert(s.begin(), x); }
void push_back(const T &x){ it=s.insert(s.end(), x); }
void push_out(SET &b){ b.push_front(back()); pop_back(); }
void pull_in(SET &b){ push_back(b.front()); b.pop_front(); }
};
/*
front(), back(), pop_front(), pop_back(), contains(x),
push_front(x), push_back(x)
ある要素の次、前を連続して得る機能 find(x), next(), Next(), prev(), Prev()
*/
multisetのラッパーのソース
template<class T> struct MultiSet{
multiset<T> s;
typename multiset<T>::iterator it;
bool empty() const { return s.empty(); }
ll size() const { return (ll)s.size(); }
void clear() { s.clear(); }
void insert(const T &x){ it=s.insert(x); }
template <class It> void insert(It b, It e){ s.insert(b, e); }
void eraseall(const T &x){ s.erase(x); } //erase all of x
void erase1(const T &x){ find(x); s.erase(it); } //erase one of x
void eraseit() { s.erase(it); }
void swap(MultiSet &b){ s.swap(b.s); }
ll count(const T &x) const { return (ll)s.count(x); }
bool contains(const T &x){ find(x); return it != s.end(); }
void find(const T &x){ it=s.find(x); }
T next() { return *(++it); }
T prev() { return *(--it); }
pair<T, bool> Next(){
if (it!=s.end()) it++;
if (it!=s.end()) return {*it,true};
else return {T(),false};
}
pair<T, bool> Prev(){
if (it!=s.begin()) return {*(--it), true};
else return {T(),false};
}
T front() const{ return *s.begin(); }
T back() const{ return *(--s.end()); }
void pop_front(){ s.erase(s.begin()); }
void pop_back(){ s.erase(--s.end()); }
void push_front(const T &x){ it=s.insert(s.begin(),x); }
void push_back(const T &x){ it=s.insert(s.end(),x); }
void push_out(MultiSet &b){ b.push_front(back()); pop_back(); }
void pull_in(MultiSet &b){ push_back(b.front()); b.pop_front(); }
};
/*
front(), back(), pop_front(), pop_back(), contains(x), eraseall(x), erase1(x)
push_front(x), push_back(x)
ある要素の次、前を連続して得る機能 find(x), next(), Next(), prev(), Prev()
*/
bit操作用クラス
bit全探索などで使う「第i bitを立てる」等のbit操作がいつまでたっても思考停止でできないので、諦めてクラスを作りました。bitsetという標準ライブラリでは、s[i]=1;で「第i bitを立てる」ができて便利そうですが、その他操作が競プロには不十分。そこで、long long に対してbit操作ができるようにしました。
これが、作ってみると超便利(当社比)! s[i]で第i bitにアクセスできるのは思考停止度高いです!また、msbを求める、立っているbitを数える、などのその他bit操作もまとめてあって便利です(当社比)。
bit操作用クラスbllのソース
struct bll{ //第0~62bitまで対応
ll s;
bll(ll s_=0): s(s_){}
struct ref {
bll &b; const ll msk;
ref(bll &b_,ll pos):b(b_),msk(1LL<<pos){}
operator bool() const { return b.s&msk; }
ref &operator=(bool x){ if(x) b.s|=msk; else b.s&=~msk; return *this; }
};
ref operator[](ll pos){ return ref(*this,pos); }
bool operator[](ll pos) const { return (s>>pos)&1; }
bll &on (ll l,ll r){ s|= rangemask(l,r); return *this; }
bll &off (ll l,ll r){ s&=~rangemask(l,r); return *this; }
bll &flip(ll l,ll r){ s^= rangemask(l,r); return *this; }
static ll rangemask(ll l,ll r){ return (1LL<<(r+1))-(1LL<<l); }
ll msbit()const{
for(ll o=63,x=-1;;){
ll m=(o+x)/2;
if (s < (1LL<<m)) o=m; else x=m;
if (o-x==1) return x;
}
}
ll lsbit()const{ return bll(lsb()).msbit(); }
ll msb()const{ ll pos=msbit(); return (pos<0) ? 0LL : 1LL<<pos; }
ll lsb()const{ return s&-s; }
ll count()const{ return bitset<64>(s).count(); }
vll idxes()const{
vll v;
for(ll i=0,t=s; t; t>>=1,i++) if(t&1)v.push_back(i);
return v;
}
};
/*
bll b(s);
b[3]=1; //第3bitを1に
b.on(4,7).off(9,59).flip(0,3); //第4~7bitを1に、等
b.s+=10; //普通に数値として扱いたい時
//0000001000101100 b
ll c=b.msb(); //0000001000000000 b.msb()
ll c=b.msbit(); // ^第9bit b.msbit()
ll c=b.lsb(); //0000000000000100 b.lsb()
ll c=b.lsbit(); // 第2bit^ b.lsbit()
ll c=b.count(); //1の数 (4個)
vll idxes=b.idxes(); //1のidxのvll {2,3,5,9}
*/
BIT(Binary Indexed Tree)のインターフェース
普通のBITのインターフェースは、一点加算add(i,x)と区間和取得sum(l,r)で、後は二分探索lower_bound(x)があるくらいかと思います。しかし、BITの用途は、集合管理であることが多いです。例えば転倒数を求める時など。
そこで、以下のように、集合に対する操作をそのまま名前にしたインターフェースを追加しました。これで思考がワンステップ減ります。
/// 集合管理向けインターフェース一覧 ///
BIT bit(n); //準備 0~n-1
ll nm=bit.size(); //集合の要素数
bit.insert(x); //集合にxを挿入
bit.erase(x); //集合からxを1つ削除
bool b=bit.contains(x); //x∈集合ならtrue
ll r = bit.rank(x); //xが小さい方から何番目か 1-origin
ll r = bit.rrank(x); //xが大きい方から何番目か 1-origin
ll nm=bit.leftnumof(x); //x以下の個数
ll nm=bit.rightnumof(x); //x以上の個数
ll nm=bit[x]; //xの個数
ll x=bit.nthsmall(r); //r番目に小さい要素 1-origin ない時はN
ll x=bit.nthbig(r); //r番目に大きい要素 1-origin ない時は-1
例えば、集合にxを挿入するinsert(x)は、裏でadd(x,1)を呼んでいるだけであり、「add(i,x)があれば簡単に実現できるんだから、無駄なんじゃ?」と思ってしまう人がいるかもしれません。しかし、脳内スタックの話を抜きにしても、「可読性が上がる」「不具合が入り込みにくくなる」という効果があるので、業プロでも通用する設計法です。
BITのソース
template <class T> struct BIT_{
vector<T> v; ll N;
BIT_(){}
BIT_(ll N) { init(N); }
void init(ll N) { v.resize(N+1); this->N = N; }
void add(ll i, T x) { for (i++; i<=N; i+=i&(-i)) v[i]+=x; }
T sum(ll i) { T s=0; for (i++; i>0; i-=i&(-i)) s+=v[i]; return s; }
T sum(ll i, ll j) { return sum(j)-sum(i-1); }
T sum() { return sum(N-1); } //総和
T operator[](ll i) { return sum(i,i); }
ll lower_bound(T s){
ll i=0,l=1; while (l<N) l<<=1;
for(; l>0; l>>=1) if(i+l<=N && v[i+l]<s) s-=v[i+=l];
return i;
}
void Dump() { rep(i,0,N-1) cerr<<setw(3)<< i <<" "<<setw(5)<< sum(i,i) <<'\n'; }
/*---- 集合管理用I/F ----*/
ll size() { return sum(); } //要素数
void insert(ll x) { add(x,1); }//集合にx追加
void erase(ll x) { add(x,-1); }//集合からx1つ削除
bool contains(ll x) { return (*this)[x] >= 1; } //x∈集合ならtrue
ll rank(ll x) { return sum(x-1)+1; }//xが小さい方から何番目か 1-origin
ll rrank(ll x) { return sum(x+1,N-1)+1; }//xが大きい方から何番目か 1-origin
ll leftnumof(ll x) { return sum(x); }//x以下の個数
ll rightnumof(ll x) { return sum(x,N-1); }//x以上の個数
ll nthsmall(ll r) { return lower_bound(r); } //r番目に小さい要素 1-origin
ll nthbig(ll r) { return (size()<r) ? -1 : nthsmall(size()+1-r); }
//r番目に大きい要素 1-origin
};
using BIT = BIT_<ll>;
view
pythonで(numpyで?)、viewという概念があります。配列の一部をコピーせず参照だけして、それに対して操作すると元の配列が書き換わる、というものです。これをうまいこと使うと、添え字まわりの記憶量を減らせそうと思い、作ってみました。
例えば、先ほどの例の「右端をmultisetに追加」では、追加対象はA[i+K-1]です。このi+K-1という添え字が厄介で、少なくとも私には紙に書かないと導き出せません。
そこで、viewを使って、ループの先頭であらかじめ「A[i]から始まり長さ $K$ のview」Vを作ってみます。すると、追加対象はviewの末尾なので、V[K-1]とすぐに分かるようになります!ループ変数iのことを忘れられるのがポイントです。
for (int i=1; i<=N-K; i++){
view1d V(A); V.st(i).size(K); //A[i]から始まり長さKのview Vを作る
//以降はVに対して処理 (iのことは忘れられる!)
}
この例はそれほど複雑ではないので、効果は大したことなさそうに見えますが、viewはもっとややこしいものをいつもの配列操作に直してくれます。例えば配列を逆方向に見る必要があるとき、添え字で混乱してバグりがちですが、配列を逆方向に見るviewを作ればいつも通りになります。また、2次元以上の配列に対しても、任意の軸方向にviewを取れたりします。例えばA[i][j]のjを固定してiを走査するviewが作れます。
また、イテレータも作ったので、標準ライブラリの各種アルゴリズムがそのまま使えます。std::sortとか、std::max_elementとか。
更に2次元のviewも作っています。例えば、3次元配列A[i][j][k]のkを固定し、jを第1軸、iを第2軸であるかのようにアクセスできるview(つまりV[j][i]でA[i][j][k]にアクセス)なんてものまで作れます。これを応用すると、90度回転させた盤面への処理もいつもの2次元配列操作にできます。ということは、4方向の処理を別々に書かず、以下のように共通化できてしまいます!これは超便利!
view2d V(A); //Aは2次元配列
for (int d=0; d<4; d++){ //4方向をループ
//Vに対して処理
V.rot90(); //90度回転
}
…と宣伝しましたが、ここに貼るには汚くて長くて恥ずかしいソースなので(テンプレートメタプログラミングが難しくて迷走しました…)、もし興味のある方はAtCoderの私の提出を見て頂ければと…。テンプレに入れているので、どの提出にもあります。view1dIter, view1d, view2dIter, view2dの4つのクラスがメインですが、少なくともrepマクロと「array用テンプレート」(ソース参照)に依存しています…
ちなみに、C++20ではviewらしきものが追加されるようなのですが、同じものなのかはいまいち分かっていません2。
もし全て○○なら△△する
「もし全て○○なら△△する」と「もし1つでも○○なら△△する」は、自分にとっては実装混乱度が高いです。考察段階、というか日本語の状態では一言で済むのに、実装しようとすると、boolを用意して初期値をtrueかfalseにして(ここで混乱)、for文回してif文書いて、ifの中の真偽で混乱し…
というわけで、「ifall」「ifany」というスニペットを用意して、なるべく日本語の流れのまま実装できるようにしています。以下はifallの例です。
{
bool allis=true;
rep(i,0,n-1) if (!(/*全てが満たす条件○○*/)) allis=false;
if (allis){
//△△する
}
}
2回使っても変数allisが2重定義にならないように、{}で囲っています。ソースが美しくない気がしますが、実装速度のためなら犠牲にします!
日本語コーディング
ライブラリの話ではないですが、実装がものすごく複雑な時の対処法を。これは業プロでいつもやっている方法で、競プロでも頭がパンクしたら使っています。
業プロだと、考えたアルゴリズムをすぐ実装完了できるわけではなく、日をまたぐのが普通です。1か月単位でかかることもあります。更に実装途中で別の仕事が入ることもあります。脳内スタックは当然消えます。久しぶりに自分の書きかけソースを見て、何をしていたのか思い出せず愕然としたりします。
この苦しみを何とかしたくて対処法を編み出しました。我流なので、もっと良い一般的な方法論みたいなものがありそうですが、自分はこの方法で仕事の効率が相当上がったので、おすすめです。
対処法は、脳内スタックを、可読性の高い方法でメモするというものです。と言っても単純で、スタックに積む代わりに、インデントして書くだけです。先ほどの脳内スタックの様子の、はじめの3つ(1つ目:1~3、2つ目:1-1~1-3を積んだところ、3つ目:1-3-1~1-3-3を積んだところ)をメモすると、以下のようになります。
↓ 1~3をメモ
区間を左端から右端までずらしながら
区間max、minを得る
max-minの最小値を更新
↓ 1を検討して出てくる1-1~1-3をメモ
区間を左端から右端までずらしながら
for文の範囲は?
あらかじめ先頭をmultisetに入れなきゃ
区間を1つずらすには?
区間max、minを得る
max-minの最小値を更新
↓ 1-1~1-3を検討して、変更したり削除したり追記したり
あらかじめ先頭をmultisetに入れる
区間を左端から右端までずらしながら
for文の範囲は?
0~N-K
あらかじめ先頭をmultisetに入れなきゃ
区間を1つずらすには?
i=0の時はずらさないからi=1~にかえなきゃ
左端をmultisetから削除して
右端をmultisetに追加
区間max、minを得る
max-minの最小値を更新
連鎖的に考えたことは、インデントしてメモしていきます。インデントしておくと、エディタの機能で折りたためるのが超ポイントです!枝葉のメモでごちゃごちゃになっても、折りたためば大筋の流れが一目で分かります。
また、「脳内スタックのメモ」と書きましたが、実際には単なる脳内スタックのメモではなく、実装内容のメモになるよう整形します。どんな風に整形するかというと、親インデントの内容の詳細が、子インデントになるようにします。インデントを折りたたむと概要が一望でき、インデントを展開するとその詳細が出てきて、更に展開するとそのまた詳細がでてきて…となるようにしたい。例えば今回の例では、最終形はこんな感じになりました。
ループ前準備
Aの先頭K個をあらかじめmultisetに入れる
区間を左端から右端までずらすループ i=1~N-K
区間を1つずらす
左端をmultisetから削除
削除対象:A[i-1]
1つ削除はfindしてからerase
右端をmultisetに追加
追加対象:A[i+k-1]
追加はinsert
区間min、maxを得る
multisetのminを得るには、先頭を見る
先頭のイテレータがbegin()
その値だから、*を付ける
multisetのmaxを得るには、末尾を見る
末尾の次のイテレータがend()
一つ前が末尾だから、--でデクリメント
その値だから、*を付ける
i=0の場合も拾う
あらかじめ先頭K個をmultisetに入れた時にも同じ処理を入れる
max-minの最小値を更新
ansをループの外に用意
chminで更新
私の使用しているエディタでは、折りたたんだ状態から展開していくと以下のようになります。

↓ 展開

↓ 更に展開
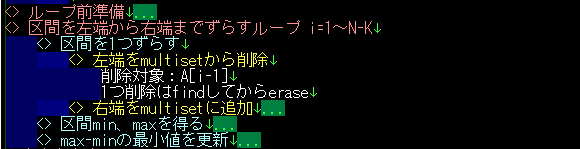
↓ 全部展開
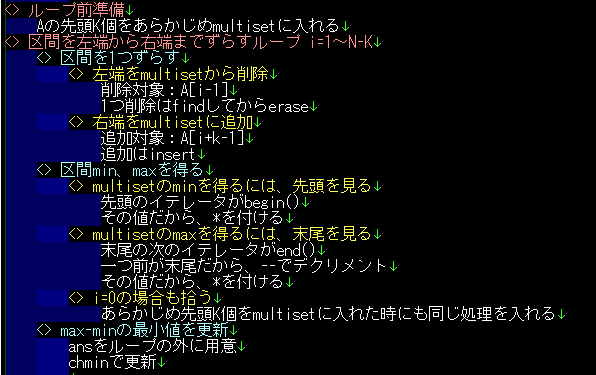
一番上の画像だと、実装の概要が簡単に理解できます。では「区間を1つずらす」の詳細は?と展開してみると次の画像になり、これもすっと頭に入ってきます。では更に「左端をmultisetから削除」の詳細は?と展開すると、次の画像になり、これも簡単に理解できます。
実装内容を丸ごと理解しようとすると混乱しますが、段階的に細かくなるように見ていくととても頭に入りやすいです。「親インデントの内容の詳細が、子インデントになるようにする」というのは、ややこしい内容を整理する上でとても重要だと思います。
記載の順序は、必ずしもソースコード上の順序と一致していなくても良いと思います。むしろ、一致させようとするとメモが理解しにくくなってしまうようであれば、一致させない方が良いでしょう。今回の例では、最後の画像の下から5行目「i=0の場合も拾う」の部分、実装時は「ループ前準備」のところに入りますが、メモ段階でそちらに入れると煩雑になるのでやめました。
記載の細かさは、ここから先はソラでコードを書けるという粗さで止めておくのがよいです。この例では説明の都合上かなり細かいところまで書いてますが、ここまではいらないと思います。
業プロで使うときは、インデントごとに入力・出力・状態変化を書いています。より整理され、順序を入れ替えたり関数化したりしやすくなります。(ここも超重要ポイントですが、競プロだとそこまで必要にならないので詳細は割愛)
また、業プロでは、何日もかけて実装を進めた後で失敗方針と分かり、大幅変更が必要になったりします。途中まで書いたソースの変更はかなりの苦行です…。しかしいきなり実装するのではなく、このメモ法でメモを作ろうとすれば、たいていの失敗方針は検出できます。ソースの変更より日本語の変更の方がずっと楽です。
イメージとしては、頭の中にあるアルゴリズム → 日本語で中間コード化 → ソースに変換、という感じです。ソースへの変換は、競プロ方言で言えば「典型やるだけ」、単なる作業になります。日本語で中間コード化するところが一番大事で、ここを日本語コーディングと呼んでいます。競プロだと、頭の中にふわっとアルゴリズムが思いついたら、後はソースをいじりながら考えることが多いと思いますが、そのフェーズを日本語でやるということです。
ちなみに、エディタは「秀丸エディタ」を購入して使っています。いにしえの素晴らしいエディタです。今のエディタなら折りたたみは当然かもしれませんが、20年前だとあまりなかったのではないかと思います。インデントの深さで色が変わるようにカスタマイズすると、とても見やすいです。
このメモ法は、日本語コーディングに限らず使えます。文章を書く時にも便利ですし(この記事もそうやって書いてます)、ややこしいことを検討するときに思考を整理するのにも超便利です。
ここまで意気込んで書いてきましたが、やっていることは単純なので、既に多くの人がやってそうに思えてきました…。まあしかし、会社では他にやっている人を見たことがないので、コロンブスの卵かもしれません。この記事を読んでこのメモ法を取り入れてくれる人がいたら大変嬉しいです!3
考察精進について
よくいわれるように、考察力を上げるには難しめの問題をじっくり考えるのがいいと思います。自分はもともと難しい問題をのんびり考えるのが好きなので、考察精進だ!と特に意識することなく、結果的には考察精進ばかりしてました。
難易度帯は、橙diffばかりやっていました。2020年8月に、kenkooooさん主催の🍊狩りバチャ(橙diffを解きまくるバチャ)に参加し、それ以来何となく橙diffにこだわりができて粘着してました。今は橙diffを考察しつくしてしまったので、黄diffと、最近のARCの全完、をメニューにしています。
考える時間は、風呂、寝る前、散歩、がメインです。この中で散歩が超おすすめです。散歩は、在宅勤務が増えて明らかに不健康になってきたので、運動不足解消のために始めました。ついでに考察精進もできそうだな、と思ったのも散歩を選んだ理由です。これが、実際にやってみると大ヒットでした。散歩中はめちゃめちゃ考察がはかどる!
考察のはかどり度合は、
散歩 ≧ 風呂(壁にタイル有)>> 風呂(壁にタイル無)>> 寝る前
です。散歩最強です!風呂も、昔はとてもはかどると思ってました。しかし、最近風呂の壁のタイルがなくなったので考察しにくくなってしまいました。タイルがあると、そのマス目に色々思い浮かべられるので考察しやすかったようです。
コンテスト中の考察方法について
精進では高難易度が解けるのに、本番では何で解けないんだろう、と思ったことありませんか?結構多くの人が思ったことあるんじゃないかと思います。自分も常々思っていました。いろんな理由がありそうです。
- 最近の問題の方がdiffが低く出るから?
- 精進時は思っているより時間がかかっていて本番では間に合わないから?
- 本番は時間が気になって頭が真っ白になりがち?
自分はコンテスト終了後に風呂に入るのですが、湯舟に浸かっていると、解けなかった問題があっさり解ける、ということがよくあります。やっぱり精進の時の何かが考察をはかどらせているようで、でもそれって何だろう、とある時考えて、一つの仮説が浮かびました。
ARC105終了後、Cは考察ミスと判明。再考しても解法浮かばず、Dも証明できず、1時間悶々としていた。しかし、諦めて風呂につかるとポンポン閃いて、全部解決した気がする。不思議だ。仮説:紙に書くと、書いてあることに引っ張られて自由な思考を妨げるからか?提案法:考察時は紙に書かない?!
本番中は紙に書いて考察していましたが、その情報が視覚から常に入ってくるので、書いた図から外れた発想・思考がしづらくなってそうだなと思いました。それを防ぐには、多くの人がしていると思われる「いろいろな図を書きまくる」という方向性ももちろんあるのですが、自分は風呂の状況を再現する方向にしてみました。つまり、目の前の壁をぼーっと見るです。
この作戦はうまくいっているような気がします。これによってぐんぐんレートが伸びた!…とは言えないので、言葉が濁ってしまいますが、少なくとも精進の時と同じような考察没頭状態に入れるようになったので効果があるのではないかと思います。
おそらく、紙に書いた方がよい局面と、頭でイメージした方が良い局面がありそうです。現状は、
- まずは紙で考察
- すぐに解き筋が浮かばない時はイメージに切り替える
- 閃いたら紙に戻って整理し、実装
としています。イメージの途中で紙に戻ったり、またイメージに戻ったりを繰り返すこともあります。紙からイメージに切り替えた瞬間は、すぐにはイメージが構築できないので、後戻りをしている感じがして焦ります。が、そこは落ち着いて乗り切ります。
さて、実はもう一つ現在試行錯誤中の考察方法がありまして、それは「散歩考察の再現」です。上でも書きましたが、散歩時の考察力はほんとすごいです。是非本番でも再現したい。「歩きながら」がポイントな気がするのですが、試しに部屋の中でうろうろしてみると、なんかあまり集中できません…。当初は、狭すぎて2,3歩しか歩けないからか?と思っていました。
再入黄できた大成功AGCの時も、C問題を考えながらうろうろしてみました。その時に、「すぐ目の前で物が(相対的に)動き、視覚刺激がきつくて集中がそがれる」ような気がしたので、明かりを消してみました。これが思いの外良かったようで、少なくともその後は集中して考察できた気がします。
というわけで、「明かりを消してうろうろする」が現状の考察案です!
…
いや、まだ本物の散歩とは程遠い気がします…
残る作戦としては、「風呂場(タイル有)での考察の再現」があります。本番中に目の前の壁を見ても真っ白なので、ここにタイル状の模様を入れた方がイメージを作りやすそう。これは効果あるだろうな、と前から思ってましたが、行動力がないのでまだ手付かず…。近々やりたいです。
おわりに
ここまで読んで下さった方、ありがとうございました。目新しい(変な?)内容が多かったと思いますが、何か1つでも刺さるものがあったら嬉しいです。
-
https://cpprefjp.github.io/reference/set/multiset/contains.html ↩
-
会社でも長年布教しているのですが、取り入れてくれた人は一人しかおらず… 秀丸をカスタマイズしすぎているから、敬遠されてしまうのかな… VSCodeなどの最新エディタならカスタマイズなしで実現できたりしないかな… ↩