大量のコンテンツをラインアップする際の有効カタログサイズ

Netflixの研究者らが発表した推薦システムの運用と改善に関する論文¹で、有効カタログサイズ (Effective Catalog Size: ECS)というおもしろい概念が提案されていたので、備忘録的にまとめます。
（この記事はZOZOテクノロジーズAdvent Calendar 2018その3の3日目の記事です）

#推薦システムの重要性
Netflixは膨大な数のビデオをラインアップしているため、ユーザーがカタログを一つ一つチェックしながら好みのビデオを見つけるのは困難です。せっかく良質なビデオをたくさんそろえても、ユーザーがそれを発見できなくては意味がありません。したがって、Netflixにとって推薦システムは"core to our business"であり、極めて大きな役割を果たしています²。
これは他の多くのIT企業も共通して抱えている問題で、音楽、本、レストラン、求人、旅行先など、現代社会において推薦システムの応用先は枚挙にいとまがありません。

###多様なコンテンツを届ける
テレビのビジネスモデルが、誰もが好むような少数のコンテンツを大多数のユーザーに届けるというものであるのに対し、Netflixは、ニッチなコンテンツを大量にそろえ、それらを好むユーザーに対して的確に届けることで大きな利益を生み出します。よって、Netflixの推薦システムは単純に人気の高いコンテンツを勧めるのでなく、多様なコンテンツを多様なユーザーに届けることが重要です。

#有効カタログサイズとは何か
では、ユーザーが消費しているコンテンツの多様性をどのように定量化すればよいでしょうか。そこで上記論文で提案されていたのが有効カタログサイズ（ECS）です。
以後、映画タイトルや楽曲などユーザに推薦する単位をアイテム、アイテムすべての集合をカタログと呼ぶことにします。
カタログに$N$個のアイテムがあり、それぞれが一定期間内に消費された割合³をベクトル$\mathbf p = [p_1, \ldots, p_N]$で表すことにします。ただし、$\mathbf p$の要素は大きい順にソートされているとします（$p_i \geq p_{i+1}$）、また割合であるため総和は1となります($\sum_{i}^Np_i=1$)。ここで、$\mathbf p$はどのアイテムが消費されやすいかを表す確率質量関数（probability mass function）として解釈できます。
この時、ECSは以下の式で定義されます。
$$
ESC(\mathbf p)=2\left(\sum_{i=1}^Np_ii\right)-1
$$
Python3での実装

def ECS(pmf):
    ecs = 0
    for idx, prob in enumerate(sorted(pmf, reverse=True), 1):
        ecs += prob*idx
    return 2*ecs -1   

アイテムが3つあるシナリオ($N=3$)で値を確認してみます。

# 1つのアイテムが圧倒的人気
p = [1, 0, 0]
ECS(p)
Output: 1

# 3つのアイテムが平等に消費される
p = [1/3, 1/3, 1/3]
ECS(p)
Output: 3

ECSは、消費されるアイテムに偏りが大きいほど最小値の1に近づき、逆にアイテムが平等に消費されるほど最大値の$N$に近づきます。つまり、ECSはユーザーが消費したコンテンツにどれくらい多様性があるかの指標となります。
上記論文の著者らは、以下の図で彼らの推薦システムの有効性を主張します（図は同論文から引用）。

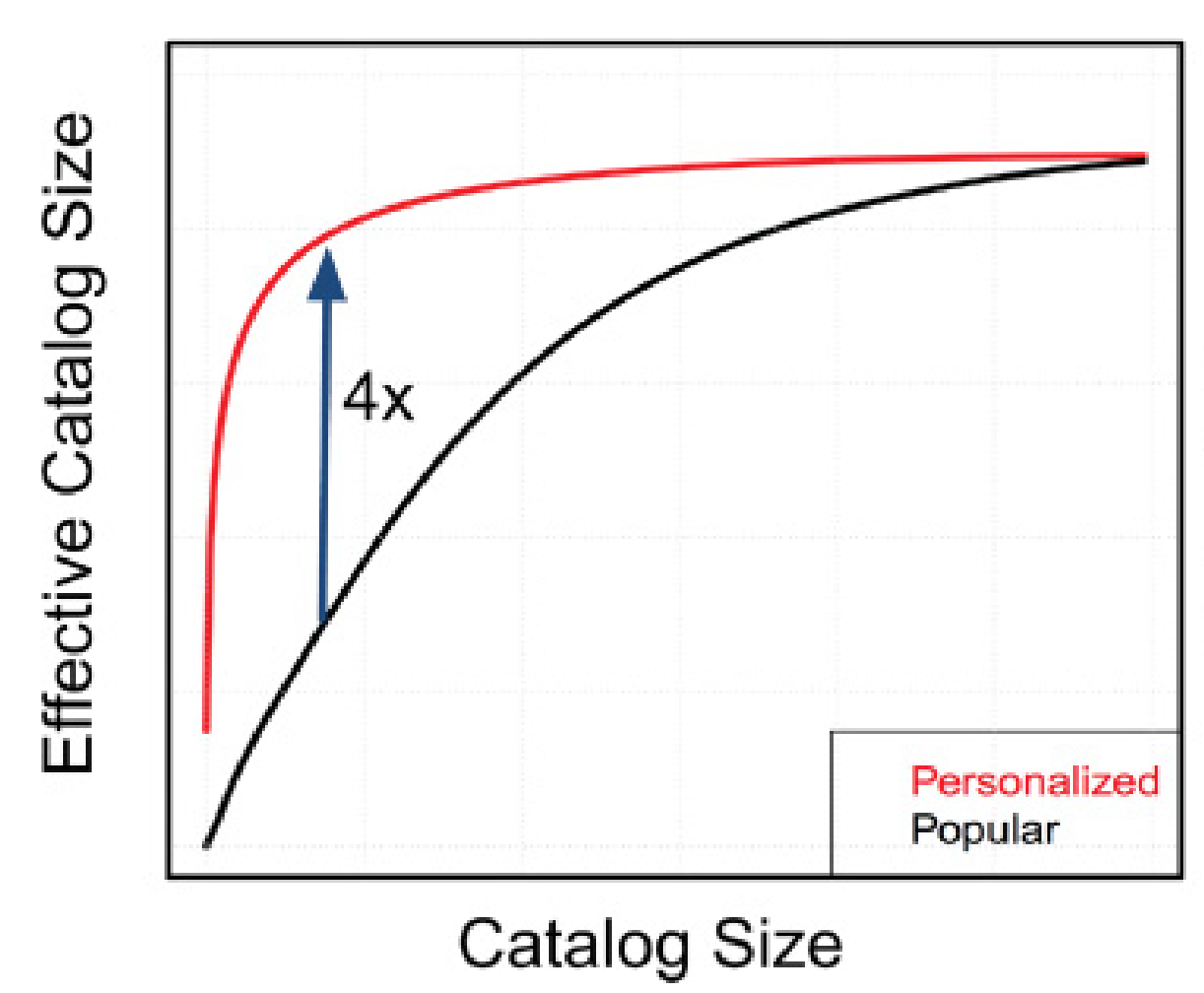
横軸にカタログサイズ、縦軸に有効カタログサイズがプロットされています。単に人気のビデオを推薦した場合が黒、推薦をパーソナライズした場合が赤でプロットされており、推薦のパーソナライズによりECSが最大で4倍になったという主張です。つまり、単に人気のコンテンツを推薦しているとユーザーはより同一のコンテンツを視聴するようになり、推薦をパーソナライズするとより多様なコンテンツを視聴するようになったことを意味します。これは、上述の通りNetflixのビジネスにとって重要なことです⁴。

おわりに

有効カタログサイズ (ECS)という概念を紹介しました。大量のコンテンツをラインアップしている状況において、どれくらい多様な選択肢をユーザーに届けることができているかの指標として使えそうです。弊社の事業領域であるファッションも多様性が非常に重要であると考えているので、今後ZOZOTOWNやWEARの有効カタログサイズを計算してみたいと思います。今回参考にした論文には、有効カタログサイズ以外にもおもしろい話が紹介されているので、興味のある方には一読を勧めます。

1. Gomez-Uribe, Carlos A., and Neil Hunt. "The Netflix Recommender System: Algorithms, Business Value, and Innovation." ACM Transactions on Management Information Systems, 2016. https://dl.acm.org/citation.cfm?id=2843948 ↩

2. 上記論文によると、ネットフリックスにおいては視聴時間の3分の2が推薦システム経由であり、年間10億ドル以上の効果をもたらしているそうです。 ↩

3. たとえば、視聴時間やクリック数の割合などが考えられます。 ↩

4. 統計的思考に慣れている人なら「有効カタログサイズなど持ち出さなくても単にアイテム消費の分散を計算すれば良いのでは？」と思うかもしれません。たしかにそれも1つの手段ですが、分散は異なるカタログサイズの間で比較が難しいという欠点があります。つまり、カタログサイズ=10の時の分散とカタログサイズ=1000の時の分散では、値が同じでも状況は大きく違います。ECSは、元のカタログサイズを基準にした上でどれくらいの多様性があるかを直感的に表現する値と言えます。 ↩