Go Advent Calendar 2015 その2 の 11日目の記事です。
Go Advent Calendar 2015 の本日の記事 → Golangで画像をglitchできるライブラリの紹介
Go Advent Calendar 2015 その3 の本日の記事 → Goのインタフェースがパフォーマンスに及ぼす影響
最近Goで書かれたアルゴリズムとデータ構造のライブラリを読み漁っていて、型と振る舞いを挿げ替えできるライブラリを作る方法を学んだのでノウハウを記事にしました。今回は題材として点更新+区間参照のシンプルなセグメントツリーを扱います。
まずセグメントツリーの概要を述べ、愚直な実装を示した後にそれを汎用化します。
セグメントツリーとは
数値が格納された配列をイメージしてください。配列は、単一要素に定数時間でアクセスでき、参照/更新のコストは共に $O(1)$ です。
しかし、区間に対する参照 ―配列の特定の区間に対する最小値を求めるとか― の場合は区間の値を一つずつ調べるしか方法がなく、配列長を $n$ とすると $O(n)$ の計算量となります。データの更新と共に調べる操作をたくさんこなす場合、配列が大きい場合は無視できない時間になります。
セグメントツリーとは、単一データの更新、区間データの参照を両方 $O(logn)$ で達成するデータ構造です。
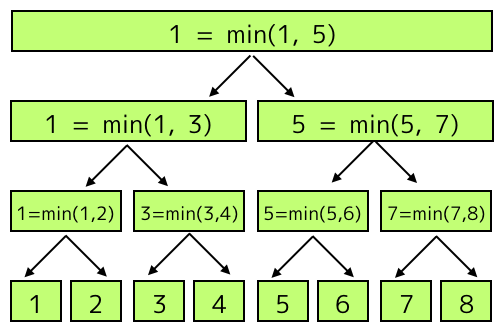
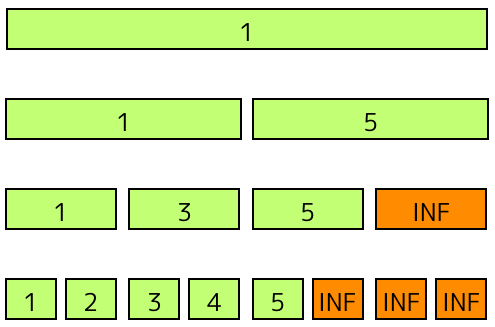
例えば、[1, 2, 3, 4, 5, 6, 7, 8] という数列と、区間に対する最小値を求めるセグメントツリーは以下のようになります。
一番下の段が生の数列。そこから一段上がると、区間が2倍に増えます。区間に書かれている数値は、左右の子の値の小さい方です。これを、区間が全体になるまでくり返します。すると、各パーツの値が数列の区間における最小値に対応します。
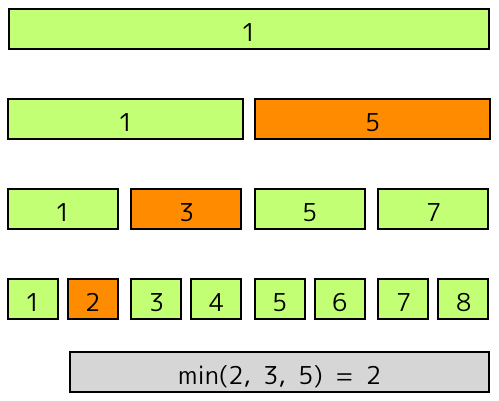
区間データの参照
指定された区間を、ツリー上の区間で「受け止め」、区間に書かれている数の最小値が答えになります。このとき受け止める区間の数は、高々木の高さの定数倍となります。
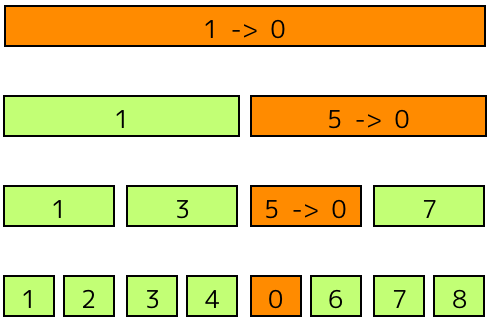
単一データの更新
データを更新する場合は一番下から初めて、対象を含む区間の値を更新していきます。このときに更新すべき区間の数は、高々木の高さとなります。
愚直な実装
以上の要件を愚直に実装したものが ここ(Go Playground) においてあります。数値をいろいろ変えて試してみてください。
以下は、上記実装の詳細な解説になります。コードと合わせて読んでください。中身に興味のない方はこの項目を飛ばしても構いません。
InitSegmentTree(セグメントツリーの初期化)
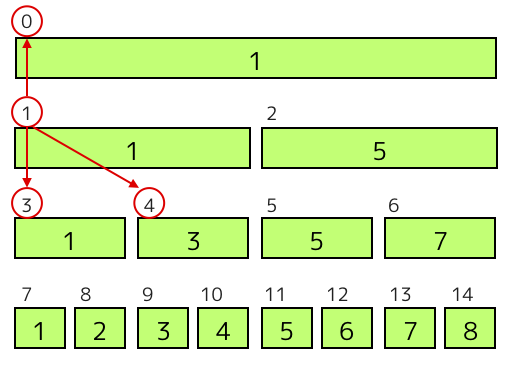
セグメントツリーの実装において、データを持つ部分は配列にするのが便利です。こうすると、左右の子や親へのアクセスが簡単になります。下の図で、
- (親の番号) = ((自分の番号) - 1) / 2
- (左の子の番号) = (自分の番号) * 2 + 1
- (右の子の番号) = (自分の番号) * 2 + 2
となっていることを確かめてください。
また、要素数がちょうど $2^n$ にならないときは、ダミーデータとして適当な大きい数値(INF)で埋めることにします。
区間のデータを計算するには、この時点でスライス上の全データが埋まっている必要があるので、この段階で埋めておきます。後ろから埋めていくのが実装的に簡単かと思います。
GetRange(区間最小値の計算)
GetRange は、getRange を呼ぶだけの関数です。getRange の意味はコメントにも書いたとおり
// [from,to)間での最小値を返す。
// 今ツリー中で見ているのはスライス上のindex番目で、それは[left,right)に相当する範囲である。
です。最初に呼ばれるときは index=0, left=0, right=tree.offset で、これは全区間を表しています。以降は次の場合分けで処理が進みます。
欲しい区間([from, to)) と [left,right) が被ってない時
この区間は見る必要が無いので、ダミー値を返します。
欲しい区間 が [left,right) を覆っている場合
左右の子に分ける意味が無い(左右に分けた子も、[from,to)が覆い尽くすため)ので、今見ているスライスの値を返します。
それ以外の場合
左右の子に対してgetRange をそれぞれ呼び、その最小値を返します。
UpdateAt(単一の値を更新する)
こちらは GetRange に比べたら実装は簡単かと思います。
- (親の番号) = ((自分の番号) - 1) / 2
- (左の子の番号) = (自分の番号) * 2 + 1
- (右の子の番号) = (自分の番号) * 2 + 2
となることに気をつけて、一番下の番号から、値を更新しながら上に登っていきます。全区間(番号0)まで到達したら終了です。
共通部分をまとめる
ここからが本題です。まず、上で紹介した実装には、以下の関数に「2つの数の最小値を取る」という部分が共通して出てきます。
- InitSegmentTree
- getRange
- UpdateAt
鬱陶しいので、これらを関数に切り出しましょう。このようになりました。
func IntMergerMin(a, b int) int {
if a < b {
return a
}
return b
}
ポイントは各所からこの関数を直接呼ぶのではなく、SegmentTree型にこの関数の型を埋め込むことです。
type Merger func(a, b int) int
type SegmentTree struct {
offset int
inf int
data []int
merge Merger
}
こうすると、InitSegmentTree関数にマージの仕方を与えることができます。
func InitSegmentTree(a []int, inf int, merge Merger) *SegmentTree {
n := len(a)
size := 1
for size < n {
size *= 2
}
data := make([]int, size*2)
for j, i := 0, size-1 ; i < size+n-1 ; i++ {
data[i] = a[j]
j++
}
for i := size+n-1 ; i < size*2 ; i++ {
data[i] = inf
}
// merge関数を使う
for i := size-2 ; i >= 0 ; i-- {
data[i] = merge(data[i*2+1], data[i*2+2])
}
// 初期化時にmerge関数を与える
return &SegmentTree{
inf: inf,
offset: size,
data: data,
merge: merge,
}
}
すると、getRange関数やUpdateAtで、SegmentTree型に定義されたmergeが使えます。まず、getRange関数は最後のif文が不要になります。
func (tree *SegmentTree) getRange(from, to, index, left, right int) int {
if to <= left || right <= from {
return tree.inf
}
if from <= left && right <= to {
return tree.data[index]
}
med := (left+right)/2
lvalue := tree.getRange(from, to, index*2+1, left, med)
rvalue := tree.getRange(from, to, index*2+2, med, right)
// merge関数を使う
return tree.merge(lvalue, rvalue)
}
UpdateAt関数は以下のように、値の更新時にmergeが使えるようになります。
func (tree *SegmentTree) UpdateAt(index int, value int) {
idx := tree.offset-1+index
tree.data[idx] = value
for idx >= 1 {
parent := (idx - 1) / 2
left := parent * 2
right := parent * 2 + 1
// merge関数を使う
tree.data[parent] = tree.merge(tree.data[left], tree.data[right])
idx = parent
}
}
このセグメントツリーを実際に使うには、InitSegmentTree関数の引数を一つ追加するだけです。これを改造して区間の最小値ではなく最大値を得るように変更するのは容易かと思います。
// 上述のIntMergeMinが定義済とする
func main() {
seg := InitSegmentTree([]int{1, 9, 5, 3, 7, 2, 4, 6, 8}, int(1e9), IntMergerMin)
fmt.Println(seg.GetRange(1, 2))
fmt.Println(seg.GetRange(3, 5))
fmt.Println(seg.GetRange(0, 9))
fmt.Println(seg.GetRange(5, 7))
fmt.Println(seg.GetRange(2, 4))
seg.UpdateAt(1, 2)
seg.UpdateAt(2, 11)
fmt.Println(seg.GetRange(1, 4))
}
intでない型に対応する
本題その2です。
現在の実装では、区間が持つ値はint型にしか対応していません。できれば、データをマージするロジックだけでなく、データの型も動的に指定したいものです。そこで、SegmentTree型を以下のように変更します。
type SegmentTree struct {
offset int
data []interface{}
inf interface{}
merge Merger
}
data が interface{} のスライスに、inf が interface{} になりました。InitSegmentTree関数は以下のようになります。
func InitSegmentTree(a []interface{}, inf interface{}, merge Merger) *SegmentTree {
n := len(a)
size := 1
for size < n {
size *= 2
}
// interface{}の配列にした
data := make([]interface{}, size*2)
for j, i := 0, size-1 ; i < size+n-1 ; i++ {
data[i] = a[j]
j++
}
for i := size+n-1 ; i < size*2 ; i++ {
data[i] = inf
}
for i := size-2 ; i >= 0 ; i-- {
data[i] = merge(data[i*2+1], data[i*2+2])
}
return &SegmentTree{
inf: inf,
offset: size,
data: data,
merge: merge,
}
}
この関数を直接呼ぶのではなく、元データを interface{} の配列に変換する補助関数を作ったほうがいいでしょう。
func InitIntSegmentTree(a []int, inf int, merge Merger) *SegmentTree {
n := len(a)
vec := make([]interface{}, n)
for i := 0 ; i < n ; i++ {
vec[i] = interface{}(a[i])
}
return InitSegmentTree(vec, inf, merge)
}
次に、マージ用の関数が interface{} を受けるように調整します。
func IntMergerMin(a, b interface{}) interface{} {
// 型アサーションでintにする
aInt := a.(int)
bInt := b.(int)
if aInt < bInt {
return aInt
}
return bInt
}
また、値を更新する関数も interface{} を受けるようにしましょう。合わせて、外から呼ぶための補助用の関数も定義してやります。
func (tree *SegmentTree) UpdateAt(index int, value interface{}) {
idx := tree.offset-1+index
tree.data[idx] = value
for idx >= 1 {
parent := idx / 2
left := parent*2+1
right := parent*2+2
tree.data[parent] = tree.merge(tree.data[left], tree.data[right])
idx = parent
}
}
func (tree *SegmentTree) UpdateIntAt(index int, value int) {
tree.UpdateAt(index, interface{}(value))
}
これにて一旦完成です。ほかの型に応用したいときはライブラリを使う側で必要に応じて、データとして持ちたい型を interface{} に変換して InitSegmentTree を呼ぶ関数や、マージ用の関数を定義してやればいいでしょう。
ここまでの実装をまとめたものが ここ(Go Playground) にあります。
応用編
セグメントツリーの各ノードとして利用可能なものは、"もの"があり、2つの"もの"を1つにマージできる関数がある ならなんでも良いことになります。(厳密に言えば、マージの順序が変わっても"もの"の値が変わらない := 結合則を満たすこと、そして単位元があること(i.e.モノイドであること)が条件です)
たとえば、整数値を格納し区間の最小を返すセグメントツリーなら"もの"と関数の対応は以下のとおりです。
- もの : 整数
- 関数 : 2つの整数をとり、小さい方を返す関数
では、もし区間の和が取りたかったら・・・?
- もの : 整数
- 関数 : 2つの整数をとり、和を返す関数
とすればよいですね。次の関数をInitIntSegmentTree関数に与えてやればいいでしょう。
func IntMergerSum(a, b interface{}) interface{} {
aInt := a.(int)
bInt := b.(int)
return aInt + bInt
}
より良い実装方法
探してます。「こうした方がいいよ」等ありましたらコメント等でぜひ教えて下さい。
まとめ
Goで異なるデータに対して同じアルゴリズムを適用するデータ構造の実装を示しました。例としてセグメントツリーを扱いましたが、グラフ等の他のデータ構造にも応用できるかと思います。
明日(12日目)の Go Advent Calendar は
- y_matsuwitter さん
- White_Raven777 さん
- Ladicle さん
の3人です。お楽しみに!