誤差逆伝播法における行列演算まとめ

1. はじめに

　誤差逆伝播法とは，ニューラルネットワークのパラメータ学習手法の１つです．考え方がシンプルであり，かつ優れた解説記事がたくさんあるので，個々のパラメータの更新式を理解するのは難しくありません．しかし，複数のパラメータをまとめて更新する場合，転置，行列積，およびアダマール積の入り混じった行列地獄にハマります．少なくとも私はハマりました．

　本記事では，誤差逆伝播法自体の説明には立ち入らず，誤差逆伝播法を行列としてどう実装するか（どんなカタチなのか）をまとめます．勉強中の身ですので，誤り等があればご指摘頂けると幸いです．

2. モデル

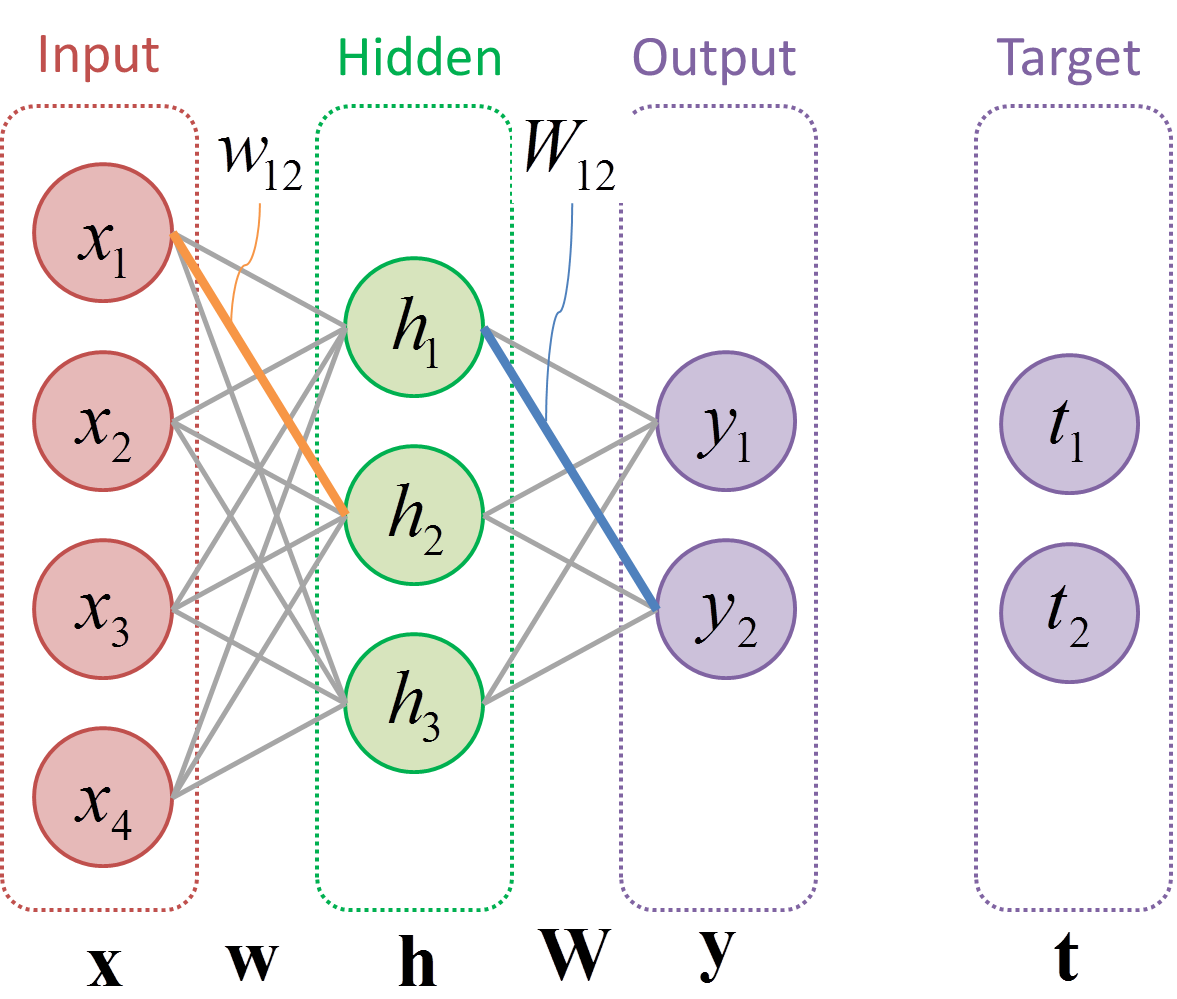
　本記事では，下図のような多層パーセプトロンの教師あり学習を想定します．

　$\mathbf{x} = \{ x_{i} \}$は入力ノード，$\mathbf{h} = \{ h_{j} \}$は隠れノード，$\mathbf{y} = \{ y_{k} \}$は出力ノード，$\mathbf{t} = \{ t_{k} \}$はターゲットノード，$\mathbf{w} = \{ w_{ij} \}$は$\{ h_{j} \}$に対する$\{ x_{i} \}$の重みパラメータ，そして$\mathbf{W} = \{ W_{jk} \}$は$\{ y_{k} \}$に対する$\{ h_{j} \}$の重みパラメータを表します．本記事では，説明を具体化するため，$i \in \{ 1, 2, 3, 4 \}$，$j \in \{ 1, 2, 3 \}$，そして$k \in \{ 1, 2 \}$と仮定します．つまり，各変数は以下のように定義されます．

\begin{align}
\mathbf{x} =& \left( \begin{matrix}
x_{1} & x_{2} & x_{3} & x_{4} \\
\end{matrix} \right) \\

\mathbf{h} =& \left( \begin{matrix}
h_{1} & h_{2} & h_{3} \\
\end{matrix} \right) \\

\mathbf{y} =& \left( \begin{matrix}
y_{1} & y_{2}\\
\end{matrix} \right) \\

\mathbf{t} =& \left( \begin{matrix}
t_{1} & t_{2}\\
\end{matrix} \right) \\

\mathbf{w} =& \left( \begin{matrix}
w_{11} & w_{12} & w_{13} \\
w_{21} & w_{22} & w_{23} \\
w_{31} & w_{32} & w_{33} \\
w_{41} & w_{42} & w_{43} \\
\end{matrix} \right) \\

\mathbf{W} =& \left( \begin{matrix}
W_{11} & W_{12} \\
W_{21} & W_{22} \\
W_{31} & W_{32} \\
\end{matrix} \right) \\

\end{align}

3. 誤差逆伝播法（要素ごと）

　まずは，要素ごとの計算式をまとめます．なお，計算式の導出については，以下の記事を参考にさせて頂きました．ありがとうございました！

誤差逆伝播法のノート
誤差逆伝播法をはじめからていねいに

3-1. 順伝播（Forward propagation）

　多層パーセプトロンは，下式に基づき，入力$x_{i}$から出力$y_{k}$を計算します．

h_{j} = \phi \left( \sum_{i} w_{ij}x_{i} \right) \tag{1}

y_{k} = \phi \left( \sum_{j} W_{jk}h_{j} \right) \tag{2}

ここで，$\phi ( \cdot )$は活性化関数を表します．活性化関数として，例えば以下のシグモイド関数がありますが，詳細は割愛します．

\phi_{\mathit{sig}} (v) = \frac{1}{1 + e^{-v}}

3-2. 逆伝播（Back propagation）

　出力$y_{k}$とターゲット$t_{k}$の誤差から，各パラメータの更新量$\Delta w_{ij}$および$\Delta W_{jk}$を計算します．詳細は割愛しますが，最急降下法（Gradient descent）と連鎖律（Chain rule）から，下式を導出できます．

\Delta W_{jk} = \delta_{k}^{\mathit{out}} \cdot h_{j} 
\mathrm{, where} \quad
\delta_{k}^{\mathit{out}} \equiv \frac{\partial \mathrm{E}}{\partial y_{k}} \cdot \phi ' \left(\sum_{j} W_{jk}h_{j} \right) \tag{3}

\Delta w_{ij} = \delta_{j}^{hid} \cdot x_{i} 
\mathrm{, where} \quad
\delta_{j}^{hid} \equiv \sum_{k} \left( \delta_{k}^{out} W_{jk} \right) \cdot \phi ' \left(\sum_{i} w_{ij}x_{i} \right) \tag{4} 

ここで，$\mathrm{E}(\cdot)$は損失関数で，例えば二乗和誤差$\mathrm{E} ( \mathbf{y} , \mathbf{t} ) = \frac{1}{2} \sum_{k} ( t_{k} - y_{k} )^{2} $ などがあります．また，$\phi'(\cdot)$は，$\phi(\cdot)$の微分を表します．
　説明のため出力層および隠れ層の誤差要素$\delta_{k}^{\mathit{out}}$および$\delta_{j}^{\mathit{hid}}$を導入しました．上の式から，出力層の誤差要素$\delta_{k}^{\mathit{out}}$が，重みパラメータ$W_{jk}$を経由して隠れ層の誤差要素$\delta_{j}^{\mathit{hid}}$に逆向きに伝播していることが確認できます．

4. 行列演算の基本

　要素ごとの計算方法は理解できました．しかし，NumPy等で実装するためには$(1)$-$(4)$の計算式を行列演算として理解する必要があります．まずは，誤差逆伝播法の実装に必要な行列演算をまとめます．

4-1. サイズとインデックス

　行列のサイズは，$m$行$n$列みたいな感じで表現します．また，行列$\mathbf{a}$の$i$行目$j$列目の要素は，$a_{ij}$と表現します．例えば，以下の行列$\mathbf{a}$は3行2列で，$a_{12}=1$です．

\mathbf{a} = 
\left(
\begin{matrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
a_{31} & a_{32}
\end{matrix}
\right) =
\left(
\begin{matrix}
0 & 1 \\
2 & 3 \\
4 & 5
\end{matrix}
\right)

4-2. 行列積

　行列積（$\cdot$）は，以下のような計算を表します．ここで，左側の行列の列数と，二つ目の行列の行数は等しくなければなりません．

\mathbf{a} \cdot \mathbf{c} = 
\left(
\begin{matrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
a_{31} & a_{32}
\end{matrix}
\right) \cdot
\left(
\begin{matrix}
c_{11}\\
c_{21}\\
\end{matrix} 
\right) =
\left(
\begin{matrix}
\sum_{n=1}^{2} a_{1n}c_{n1} \\
\sum_{n=1}^{2} a_{2n}c_{n1} \\
\sum_{n=1}^{2} a_{3n}c_{n1}  
\end{matrix} 
\right)

4-3. アダマール積

　アダマール積（$\circ$）は，要素ごとの積を表します．ここで，加算する行列同士のサイズは等しくなければなりません．

\mathbf{a} \circ \mathbf{b} = 
\left(
\begin{matrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
a_{31} & a_{32}
\end{matrix}
\right) \circ
\left(
\begin{matrix}
b_{11} & b_{12} \\
b_{21} & b_{22} \\
b_{31} & b_{32}
\end{matrix} 
\right) =
\left(
\begin{matrix}
a_{11}  b_{11} & a_{12}  b_{12} \\
a_{21}  b_{21} & a_{22}  b_{22} \\
a_{31}  b_{11} & a_{32}  b_{32} 
\end{matrix} 
\right)

4-4. 転置

　転置（$^T$）は，以下の操作を表します．ここで，操作の前後で行列のサイズが変わっていることにご注意ください．

\left(
\begin{matrix}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
a_{31} & a_{32}
\end{matrix}
\right)^{T} = 
\left(
\begin{matrix}
a_{11} & a_{21} & a_{31} \\
a_{12} & a_{22} & a_{32} \\
\end{matrix}
\right)

5. 誤差逆伝播法（行列）

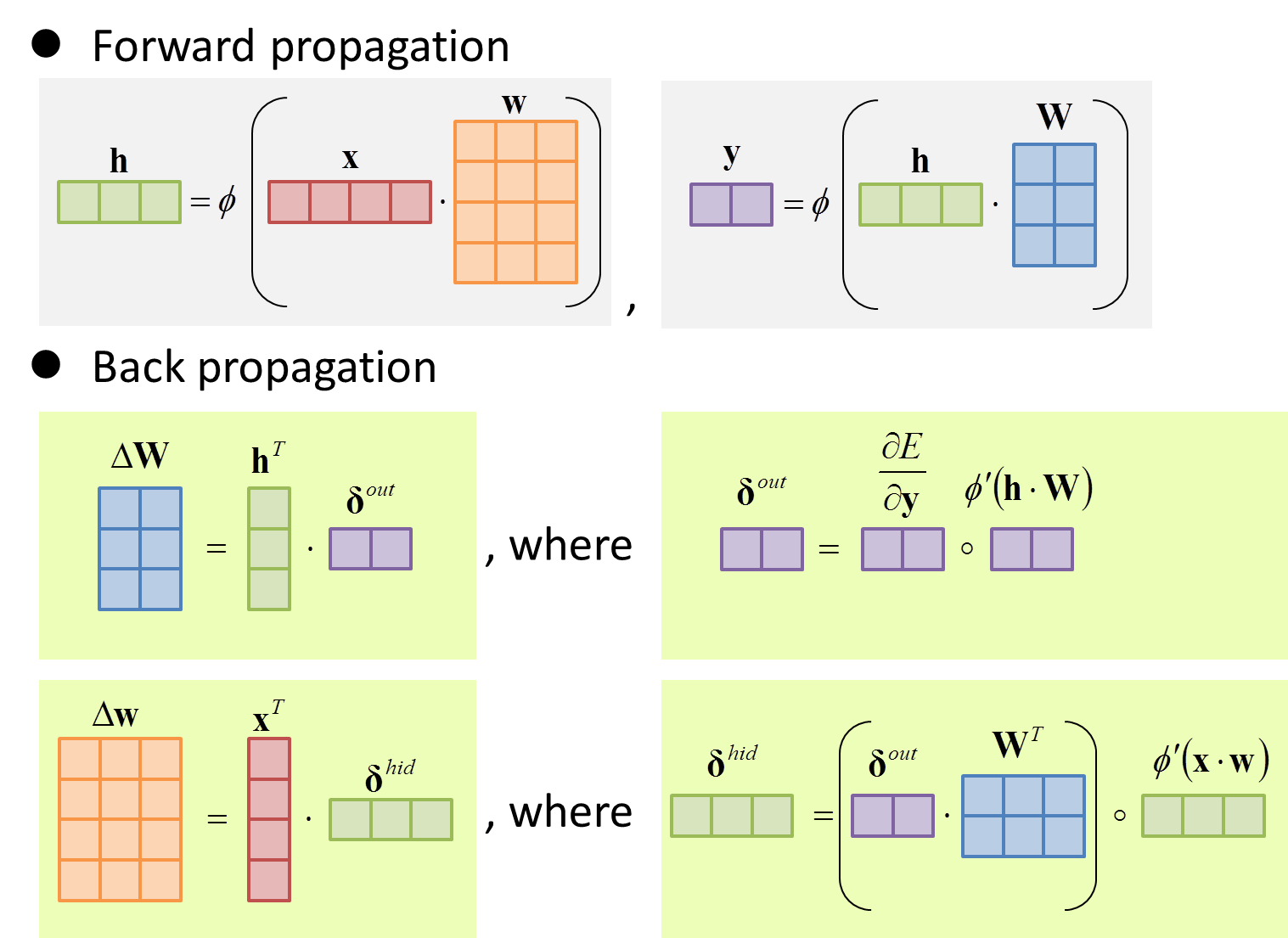
　さて，準備は整いました．本章では，3章で記載した計算式$(1)$-$(4)$を，4章で記載した行列演算を用いて表現します．

5-1. 順伝播（Forward propagation）

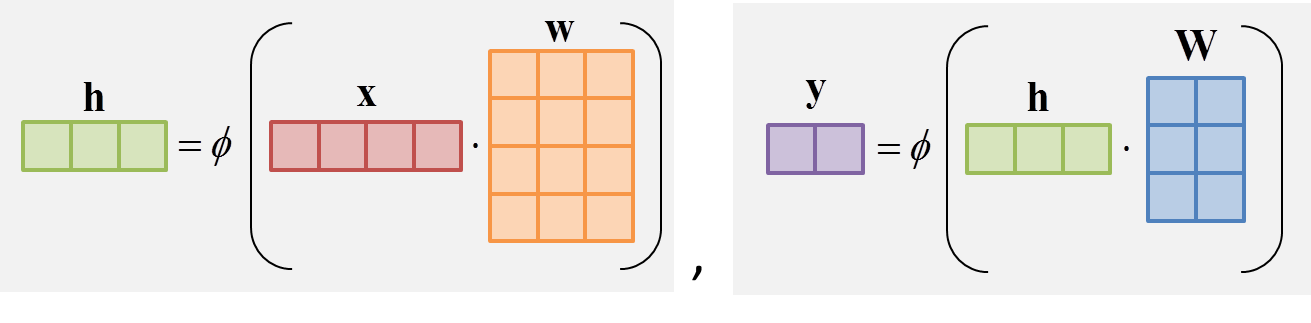
　順伝播の計算式$(1)$および$(2)$は，以下のように書き直すことができます．

\left(\begin{matrix}
h_{1} & h_{2} & h_{3} \\
\end{matrix}\right) 
= \phi \left( 
\left(\begin{matrix}
x_{1} & x_{2} & x_{3} & x_{4} \\
\end{matrix}\right) \cdot
\left( \begin{matrix}
w_{11} & w_{12} & w_{13} \\
w_{21} & w_{22} & w_{23} \\
w_{31} & w_{32} & w_{33} \\
w_{41} & w_{42} & w_{43} \\
\end{matrix} \right)
 \right) \tag{1'}

\left(\begin{matrix}
y_{1} & y_{2} \\
\end{matrix}\right) 
= \phi \left( 
\left(\begin{matrix}
h_{1} & h_{2} & h_{3} \\
\end{matrix}\right) \cdot
\left( \begin{matrix}
W_{11} & W_{12} \\
W_{21} & W_{22} \\
W_{31} & W_{32} \\
\end{matrix} \right)
 \right) \tag{2'}

行列積を使って，$\sum$を一気に計算していることがわかります．
　下図は，行列のサイズ感を直感的に表した図です．同じサイズの行列は，同じ色のブロックで表現しています．NumPyで実装する際に役に立ちました．

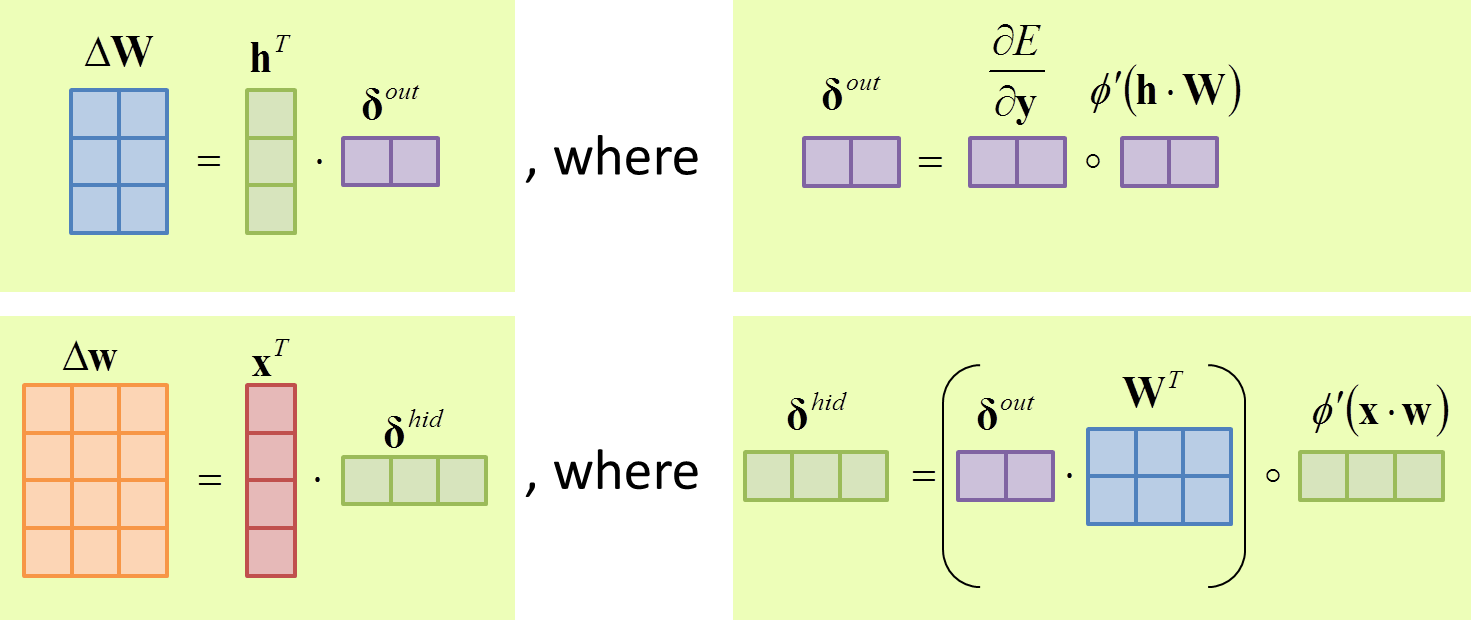
5-2. 逆伝播（Back propagation）

　逆伝播の計算式$(3)$および$(4)$は，以下のように書き直すことができます．転置，行列積，アダマール積が入り乱れ，まるで地獄のよう．

\left(\begin{matrix}
\Delta W_{11} & \Delta W_{12} \\
\Delta W_{21} & \Delta W_{22} \\
\Delta W_{31} & \Delta W_{32} \\ 
\end{matrix}\right) = 
\left(\begin{matrix}
h_{1} & h_{2} & h_{3} 
\end{matrix}\right)^{T} 
\cdot
\left(\begin{matrix}
\delta_{1}^{\mathit{out}} & \delta_{2}^{\mathit{out}} 
\end{matrix}\right) 
\mathrm{, where}\\

\left(\begin{matrix}
\delta_{1}^{\mathit{out}} & \delta_{2}^{\mathit{out}}
\end{matrix}\right)
\equiv 
\left(\begin{matrix}
\frac{\partial \mathrm{E}}{\partial y_{1}} & \frac{\partial \mathrm{E}}{\partial y_{2}}
\end{matrix}\right)
\circ 
\left(\begin{matrix}
{\phi_{1}^{\mathit{out}}}'  & {\phi_{2}^{\mathit{out}}}'
\end{matrix}\right) \tag{3'}

\left(\begin{matrix}
\Delta w_{11} & \Delta w_{12} & \Delta w_{13} \\
\Delta w_{21} & \Delta w_{22} & \Delta w_{23} \\
\Delta w_{31} & \Delta w_{32} & \Delta w_{33} \\
\Delta w_{41} & \Delta w_{42} & \Delta w_{43} \\
\end{matrix}\right) = 
\left(\begin{matrix}
x_{1} & x_{2} & x_{3} & x_{4} 
\end{matrix}\right)^{T} 
\cdot
\left(\begin{matrix}
\delta_{1}^{\mathit{hid}} & \delta_{2}^{\mathit{hid}} & \delta_{3}^{\mathit{hid}} 
\end{matrix}\right) 
\mathrm{, where}\\

\left(\begin{matrix}
\delta_{1}^{\mathit{hid}} & \delta_{2}^{\mathit{hid}} & \delta_{3}^{\mathit{hid}} 
\end{matrix}\right)
\equiv 
\left(
\left(\begin{matrix}
\delta_{1}^{\mathit{out}} & \delta_{2}^{\mathit{out}}
\end{matrix}\right)
\cdot
\left( \begin{matrix}
W_{11} & W_{12} \\
W_{21} & W_{22} \\
W_{31} & W_{32} \\
\end{matrix} \right)^{T}
\right)
\circ 
\left(\begin{matrix}
{\phi_{1}^{\mathit{hid}}}'  & {\phi_{2}^{\mathit{hid}}}' & {\phi_{3}^{\mathit{hid}}}'
\end{matrix}\right)
\tag{4'}

ここで，${\phi_{k}^{\mathit{out}}}'$および${\phi_{j}^{\mathit{hid}}}'$は，以下を表します．

{\phi_{k}^{\mathit{out}}}' \equiv　\phi ' \left(\sum_{j} W_{jk}h_{j} \right) \\
{\phi_{j}^{\mathit{hid}}}' \equiv　\phi ' \left(\sum_{i} w_{ij}x_{i} \right) 

　下図は，行列のサイズ感を直感的に表した図です．同じサイズの行列は，同じ色のブロックで表現しています．NumPyで実装する際に役に立ちました．

6. おわりに

　NumPyで実装するときとても苦労したので，誤差逆伝播法の行列演算をまとめました．実装上の行列地獄を緩和することを目的に書きましたが，作成中，皮肉にも，Tex表記という新たな行列地獄にハマってしまいました．
　最後まで読んでくださり，ありがとうございました！