木構造に対する「再帰なし」深さ優先探索 (DFS)

次のような木を考えます。

深さ優先探索で「各ノードの子孫ノードの合計数」を求めることを考えます。

通常、深さ優先探索は再帰関数を使って書くと楽です。

const std::vector<size_t> children[7] = {{5, 1}, {4}, {}, {}, {6}, {2, 3}, {}};
int64_t counts[7] = {0};

int64_t dfs(size_t node) {
  int64_t ret = 1;
  for (auto child: children[node]) {
    ret += dfs(child);
  }
  counts[node] = ret;
  return ret;
}

int32_t main() {
  dfs(0);
  std::cout << counts[0] << std::endl; //=> 7
  return 0;
}

しかし、言語や環境によっては

• 関数呼び出しが重い
• スタックの深さに制限がある
• グローバル変数を使用できない

などの理由により再帰関数を使いたくない場合があります (hakatashiが競技プログラミングで用いる言語Crystalなどがそうです)。

再帰なし深さ優先探索

幅優先探索のキューをスタックに置き換えると深さ優先探索になります。

children = [[5, 1], [4], [], [], [6], [2, 3], []]
stack = []
stack << 0

until stack.empty?
  node = stack.pop
  p node
  children[node].each do |child|
    stack << child
  end
end

Wikipediaにもこのタイプのアルゴリズムが載っています。しかしこのままだと今回のように子ノードの情報を用いてアルゴリズムをエイヤするのに不便です。

これを解消するために、まず必ず子が親の後に来るようにノードをソートします。

これは木を親から子への有向グラフとみなしたときのトポロジカルソートと同じですが、木の場合単純にDFSで訪れた順に積めばいいので楽です。

children = [[5, 1], [4], [], [], [6], [2, 3], []]
stack = []
stack << 0
sorted_nodes = []

until stack.empty?
  node = stack.pop
  sorted_nodes << node
  children[node].each do |child|
    stack << child
  end
end

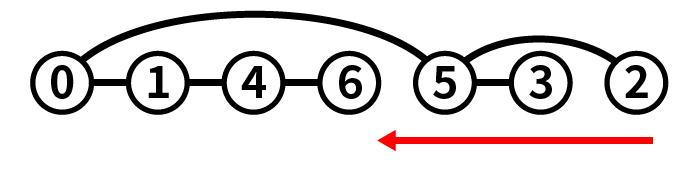
p sorted_nodes #=> [0, 1, 4, 6, 5, 3, 2]

あとはこのノードを逆順に見ていけばDFSができます。

children = [[5, 1], [4], [], [], [6], [2, 3], []]
stack = []
stack << 0
sorted_nodes = []

until stack.empty?
  node = stack.pop
  sorted_nodes << node
  children[node].each do |child|
    stack << child
  end
end

counts = Array.new(7, 0)

sorted_nodes.reverse_each do |node|
  ret = 1
  children[node].each do |child|
    ret += counts[child]
  end
  counts[node] = ret
end

p counts[0] #=> 7

全方位木DPなどで今度は親から順に見て上げる必要がある場合はふたたび昇順にループします。