データサイエンスの世界を革命する（かもしれない）symengine.py

こんにちは！　データサイエンティストのデ西園りりだよ！

今日はみんなに、symengine.pyを紹介しちゃうね！

symengine.pyはまだ歴史の浅いプロジェクトで、知名度が低いけれど、データサイエンスの世界を革命する力を秘めているよ。それは一体どういうことなのか、今から解説していくね。

Computer algebra system (CAS)

みんなは computer algebra system (CAS) って聞いたことあるかな？　数値ではなく数式を計算するシステムだよ。

• Mathematica、Maple、GNU Octave、MATLAB、一部のグラフ電卓などなどについている
• 数式をプログラムではなく数式言語で表現する
• 解析的な微分（数値微分じゃない奴）とかを計算して、数式言語で出力できる

システムだよ。Pythonだと SymPy が一番有名だね。

グラフ電卓はともかく、PCで動くCASでは、数式を数式言語で直書きするよりも、プログラムで組み立てるほうが一般的だよ。数式言語ではとても直書きできないような巨大な数式も、プログラムで組み立てれば簡単に作れるよ。

データサイエンスの第一歩は、モデル（＝数式）にデータをあてはめるフィッティングだよ。線形最小二乗法が使える特別な場合を除いて、一般的には、なんらかの非線形最小二乗法を使うよ。

非線形最小二乗法にはヤコビアン関数が必要だよ。scipyだとヤコビアン関数なしでleast_squares()を使うと数値微分するけれど、もちろんヤコビアン関数があったほうが速いよ。特に係数の多いモデルでは、ヤコビアン関数がないと、現実的な時間内ではフィッティングできないよ。

とはいえ係数の多い複雑なモデルほど、解析的なヤコビアンを計算するのは大変！　そこでCASを使えば簡単…　なんて甘い話は、これまでPythonにはなかったよ。

1. モデルをCASの数式として組み立てる
2. 解析的な微分を計算して、その結果を数式言語で出力する
3. 2つの数式を、Numpyでの処理に変換する

これを1回やるだけならいいけど、データサイエンスでは、フィッティングの結果を見てモデルをいじくりまわすよ！　3の変換がちょっとした差分とかでは済まない場合、「こんなの絶対おかしいよ」ってなるよ。複雑なモデルでは、3にはNumpyのベクトル演算を活かした最適化が必要になるからね。

そこでSymPyのlambdify()はどう？　これはまさに3をやってくれる機能だよ。でも最適化ができてない、という話をこれからするよ。

「とりあえずsymengine.pyってなんなの？」という説明をまだしてなかったね。symengine.pyは、

• SymPyの速い奴
• 特にlambdify()の作る関数が速い

だよ！　複雑なモデルでも、CASの数式として組み立てるプログラムを1回書くだけで、あとは自分で数式を触らなくていい、ということだよ！

「ホント？」

「それってどういうこと？」

という話をこれからしていくね！

Iスプライン

データサイエンスの第1法則、それは

外挿がどれくらい当たるかはわからない

だよ！

どのモデルの外挿がよさそうで、どのモデルの外挿がダメそうか、まで（定性的）はわかるけれど、どれくらい当たるか（定量的）はわからないよ。

たとえば、スプラインは外挿がダメに決まってる（定性的）よ。事の性質からして精度のいいモデルがありえない場合、スムージングと補間に使うモデルだよ。だから、スプラインで天気予報をしてはいけません。でもだからといって、外挿が当たりそうなモデル（定性的）でも、どれくらい当たるか（定量的）はわからないよ！　データサイエンスは科学。科学は厳しい！

さて警告はこれくらいにして、Iスプラインの話をするね。

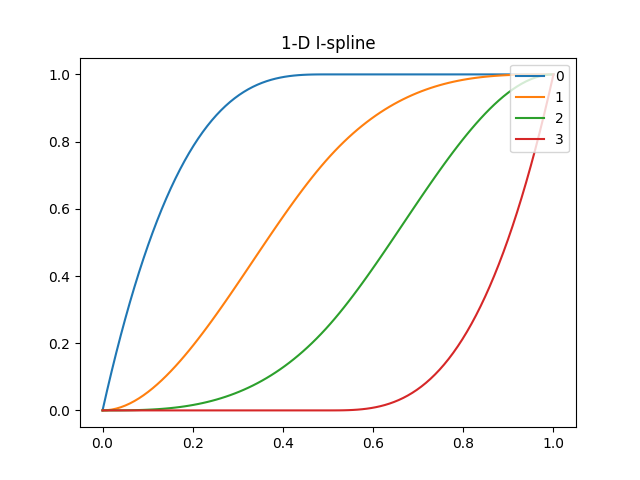
Iスプラインは単調増加のスプラインだよ。事の性質からして単調増加が明らかな場合に使えるよ。数式とかはWikipediaでも見てね。

Iスプラインにフィッティングするというのは、上の図の4つの曲線にそれぞれ異なる重み係数を掛けてから合計することで作られた曲線が、フィッティング対象のデータにできるだけ近くなるように4つの重み係数を決定する、ということだよ。その決定方法が最小二乗法ってわけだね。もしすべての重み係数が正なら、どこにも減少は起こらない、つまり単調増加だよ。

ちなみに、曲線の曲がりの位置を変えることもできるよ。でも、その係数までフィッティングに含めると、桁違いに時間がかかるよ。

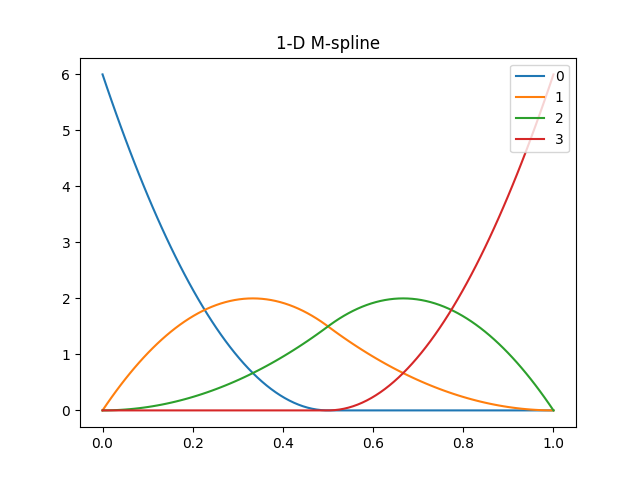
MスプラインはIスプラインの微分だよ。Iスプラインを計算するのに使うよ。

今日は、実際に使いそうな複雑なモデルとして、Iスプラインをn次元に拡張したモデルを使うよ！

ただしn次元Iスプラインにはちょっと面倒な性質があるよ。Iスプラインをy = f(x)として、xはn次元のベクトル、yはスカラーとすると、any(x == 0)のときにyが0になること。それを補うために、n次元Iスプラインからもっと複雑なモデルを作ったよ。名付けて、「hC9i」！（パスワードジェネレータで作った意味のない文字列だよ。名前をつけるのって面倒）　今日はhC9iへのフィッティングを試してみるよ。

symengine_example

symengine_exampleは

• n次元IスプラインとMスプライン
• hC9i
• 可視化
• フィッティング

を実装したデモだよ。symengine.pyとSymPyの実行速度が比較できるようにしてあるよ。Python 3.11で動かしてね。

git cloneしてpip install -r requirements.txtしたら、まずは

python -m symengine_example.visualize_spline 2 i 2d l en

2次元のIスプラインのプロットのアニメーションが表示されたね！

visualize_splineのコマンドライン引数を説明すると

1. スプラインのdegree (1|2|3)
2. MスプラインとIスプラインの選択 (m|i)
3. スプラインの次元 (1d|2d|3d)
4. 計算方法 (i|s|l)
5. SymPyとsymengine.pyの選択 (py|en)

4の計算方法は

• i: SymPyもsymengine.pyもどちらも使わず、数値をそのまま計算する

SymPyを使うプログラムは、プログラムを実行することで数式を組み立てるんだけど、そのとき変数（Symbolオブジェクト）のかわりに数値（定数）を入れるだけで、数式のかわりに計算結果の値が出力されるよ。

• s: 数式を作ってsubs()で計算する。lambdify()は使わない

subs()というのは数式内の変数を、ほかの変数や定数に置き換える関数だよ。すべての変数を定数に置き換えたら計算完了で、数式は数値になっているよ。

• l: lambdify()を使う

とりあえずはvisualize_splineでいろんなプロットを眺めて、MスプラインとIスプラインの感覚をつかんだりしてみてね。

スプラインの可視化の次は、hC9iのフィッティングだよ。

python -m unittest tests.test_model.TestModel.test_fit_params_solve_xs

これには数十秒かかるから待ってね。そして

python -m tests.test_model

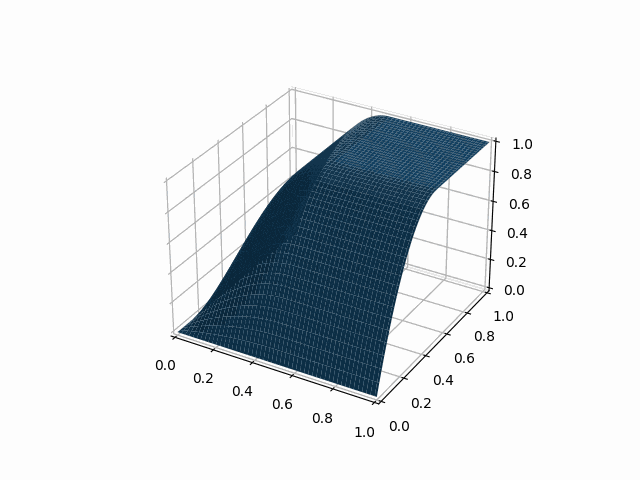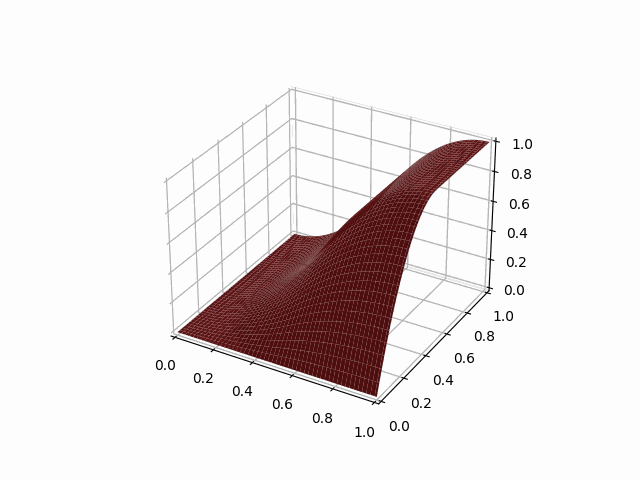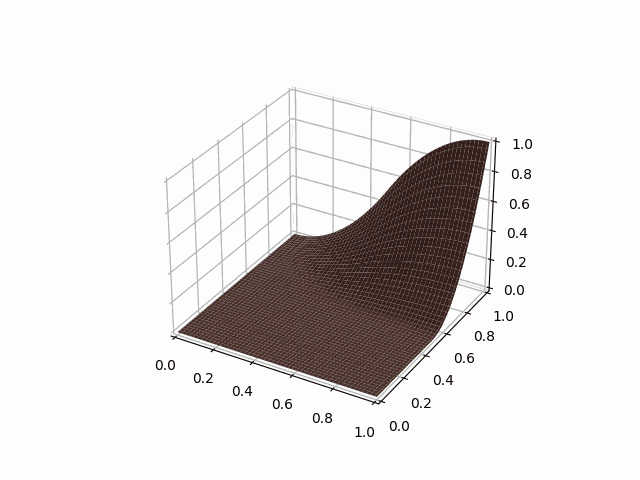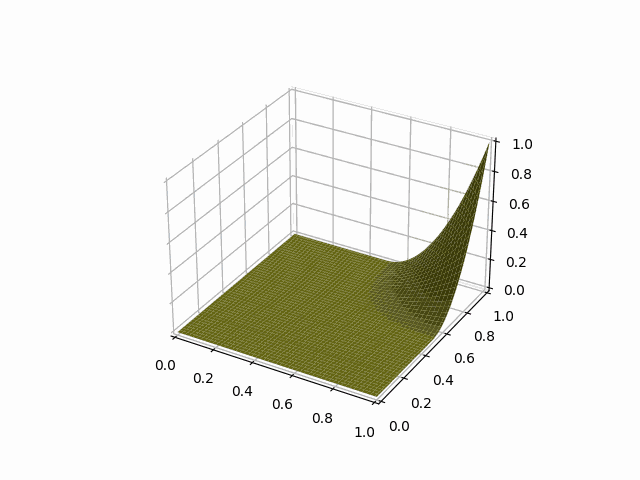
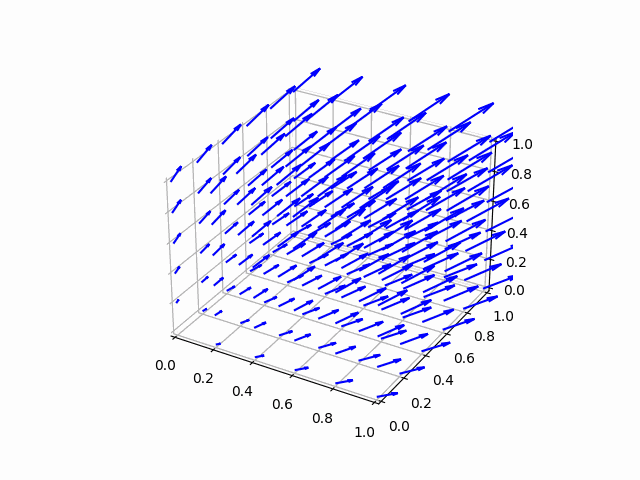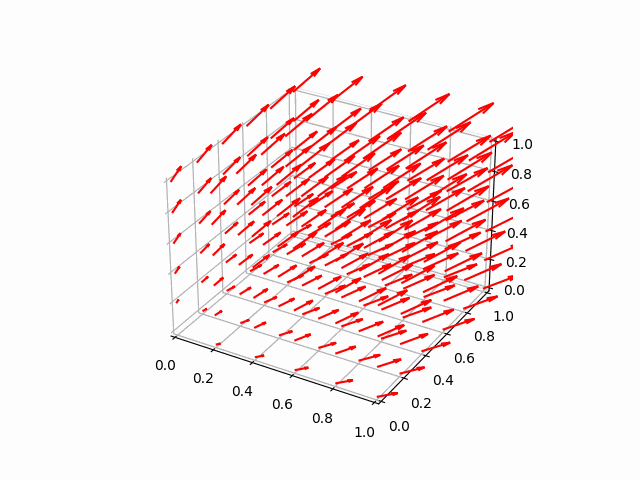
3次元ベクトル場のプロットのアニメーションが表示されたね！　青がフィッティングの対象として与えたデータ、赤がフィッティングの結果だよ。かなりの精度でフィッティングできてるのがわかるね。

SymPyとの速度の比較

いろんなケースで比較できるけれど、ここではlambdify()を使った比較的単純なモデルでの例を示すね。

$ python -m symengine_example.visualize_spline 2 i 2d l en
Total computation time: 0.8512809000094421 seconds.
    Subtotal time for function call: 0.252729299972998 seconds.
    Subtotal time for lambdify(): 0.5985516000364441 seconds.
$ python -m symengine_example.visualize_spline 2 i 2d l py
Total computation time: 83.87184929999057 seconds.
    Subtotal time for function call: 82.26858449997962 seconds.
    Subtotal time for lambdify(): 1.6032648000109475 seconds.

lambdify()にかかった時間を含めても100倍ちかく、含めなければ300倍以上、symengine.pyのほうが速いね！

「SymPyは数式をNumpyでの処理に変換するときの最適化ができてない」と上で書いたよね。これがそういうことだよ。

ちなみに、lambdify()の結果はpickleで保存できるよ。並列処理やバッチ処理では、300倍以上の差があるってことだね。

SymPyでは現実的な時間内に終わらないような複雑なモデルの計算が、symengine.pyならできるよ！

メモリ使用量

ここまで「symengine.pyはすごい！」という話ばかりしてきたけれど、ホントかな？

残念ながら、今（symengine-0.10.0）のsymengine.pyには、あれこれ厳しいところがあるよ。

まず、肝心かなめのlambdify()から見ていくね。

（Windowsなら）タスクマネージャを開いて、メモリの「コミット済み」を見ながら、python -m symengine_example.visualize_spline 2 i 3d l enを実行してみて。実行中に400MBくらいの幅の増減があり、最後には下がって止まるのがわかるね。この400MBはlambdify()が使っている分だよ。

相手が数式なのに、400MBって、ちょっと不思議なくらい多くないかな？

じゃあ次は、まずタスクマネージャ以外の他のアプリを全部閉じてね。理由はあとでね。そしたらdegreeを上げて、python -m symengine_example.visualize_spline 3 i 3d l enを実行してみよう。

あなたのPCの「コミット済み」はどこまで増えたかな？　りりは30GBまで見たよ！　そしてページファイルを全部使い切ったあと、CPUがRyzen 5 5600Xだと、Windowsごと固まるよ！　Windowsが固まったときの被害を最小限にするために、他のアプリを全部閉じてもらったんだね。

これはつまり、モデルをいじるときに、lambdify()できる範囲に収める感覚が必要になるわけで、開発体験としては厳しいものがあるよ。りりの場合、CPUがRyzen 5 5600Xだから、読み違えるとWindowsごと固まるので、さらに厳しい体験だよ！　この問題があるから、hC9iのフィッティングにはlambdify()を使ってないよ。

それにしても、どうしてCPUがRyzen 5 5600XだとWindowsごと固まるのかな？　Intelだと固まらないよ。物理メモリのあちこちをデタラメに書き換えてるような挙動だよ。たぶんCPUの脆弱性を突いてしまっているんだね。

デバッグ

VSCodeでは、ローカルかグローバル変数にsymengine.pyの数式が入っているときにブレークポイントで止めると、すごく遅い場合があるよ。なぜかというと、VSCodeのPythonデバッガはブレークするたびに、すべての見える変数に対して__repr__()を実行するんだけど（例外あり）、symengine.pyの数式に__repr__()をかけると、数式言語で中身を書き出すからだよ。

これを防ぐにはまず、RUN AND DEBUGのVARIABLESをあらかじめ閉じておくよ。そして、変数にマウスオーバーしても__repr__()がかかるから、ブレークしているあいだはマウスオーバーしないように注意！　根本的に止める方法は、ないんじゃないかな？　厳しいね！

ドキュメント

今（symengine-0.10.0）、symengine.pyはSymPyの何割かを実装しているよ。なにがあって、なにがないのかは、どこにも書いてないよ。ドキュメントが一切ないからね。

「は？」

本当だよ。まずSymPyで書いてみて動かして、それからsymengine.pyに切り替えて、動くかどうかを試すんだよ。ちなみにdocstringもないよ。最終的にはソースコードを見るんだよ。すべてがアンドキュメンテッド！　ワイルドだろぉ？

どの機能があるのかは、symengine_exampleを見ればわかるから、ない機能で重要なのをひとつ挙げると、solve()がないよ。

面倒な仕様をひとつ挙げると、subs()はNumpyのfloat64と互換性がないよ。引数にはfloat64ではなくPythonのfloatを入れないとダメだよ。すべての変数シンボルが消えて値になったときには、LLVMDoubleという型になり、これはPythonのfloatじゃないから、Pythonの組み込み関数のfloat()で型変換しないといけないよ。lambdify()すれば万事解決なんだけど、メモリ使用量問題があるから、そうはいかない場合もあるよ。

いくら速度300倍とはいえ、ドキュメント一切なしは厳しいね！　MATLAB Symbolic Math Toolboxに何十万円か出したほうがマシかもね。りりは試したことがないから知らないよ。

それってどういうこと？

今現在のsymengine.pyの厳しさをわかってもらえたところで、「データサイエンスの世界を革命する力を秘めている」とはどういうことか、手短に言い換えてみるよ。

「computer algebraとnumerical analysisを統合する」

computer algebraなしのnumerical analysisでは、数式ではなく計算をプログラミングしているよ。algorithmを「算法」と訳した例があるけれど、そんな感じだね。

symengine.pyを使えば、numerical analysisのプログラミングは、数式を組み立てるものになるよ。一種のメタプログラミングだね！　高位合成といってもいいかもね！

さらに、数式をlambdify()するという方法はCUDAカーネルの生成にも使える、ということに気づいてるかな？

計算をするバイナリは、引数が少ないほうが速くできるよ。コンパイル時定数には定数畳み込みが効かせられるからね。symengine.pyも、lambdify()はもちろん、subs()でも定数畳み込みをやるよ。

CUDAカーネルでの定数畳み込みは、計算量もさることながら、引数を読み込むメモリアクセスによるストールを避けられるから、効果が大きいよ！　CUDAカーネルでは即値（機械語命令のなかに埋め込んである値）とメモリの差は天地の差だよ。でも汎用性を持たせようとしたら、引数は多くなるよね。だからCUDAカーネルを動的に生成することのメリットは絶大だよ。その生成のフローとして、computer algebraで数式を組み立ててlambdify()する、というわけだよ！

さらにさらに、CUDAカーネルどころか、まだ見ぬHPCアーキテクチャにも使える、ということに気づいてるかな？

今すでにあるアーキテクチャでたとえると、FPGAをイメージしてみて（ただしFPGAでコスパよくアクセラレーションできる数式は珍しいと思うよ）。極端なケースでは、ビットコイン採掘のように、特定の計算を実装したセミカスタムのASICを製造することさえ考えられるよ。

将来の未知のHPCアーキテクチャでも、計算したいものはやっぱり数式で表現されるだろうし、その数式はプログラムで組み立てたいだろうし、定数畳み込みを効かせたいだろうから、computer algebraで数式を組み立ててlambdify()する、というフローは魅力的だよ！　魅力的というより、これは人類のファイナルアンサーじゃないかな？

symengine.pyが実際にSymPyを300倍以上速くするまでは、こんなヨタ話、誰も耳を貸さなかったと思うよ。でも今すでに、そのヨタ話の2割くらいは、みんなのPCの上で動くようになっているよ。symengine.pyはデータサイエンスの世界を革命する力を秘めているよ！