python で近似球を作ってみる

概要　

今回は，OPENGLで描画，実装されているコードを見つけたので，それをPythonに書き換えてみました．
この記事には，メモ程度に作っているので，ご理解お願いします．

動作環境

この記事は以下の環境で動いています。

項目	値
CPU	Core i5-8250U
RAM	8GB
Ubuntu	18.04
python	2.7
ROS	melodic

近似球って？

近似球は言葉の通り，球体を近似したもの．
英語では，icosphereとか言われているらしい．
コンピュータ上で，球体を表現，描画するときに必要な手法．
グラフィックデザイナーとかの人たちは，作成した近似球にテクスチャを貼ることで，地球儀とかを表現することができるようになるっぽい．

実際に作ってみる

具体的なスクリプトは，こちらに書いてあるものを参考にしました．
これをpythonで実装します．他の方々がもっとスマートな方法でスクリプトを作成しているのですが，今回は，近似球の各頂点を明示的にわかるようなコードにしています．

sphere.py

#!/usr/bin/env python3

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

radius=1.0
sectorCount=20
stackCount=20

xx=[]
yy=[]
zz=[]

lengInv=1.0/radius
sectorStep = 2* np.pi/ sectorCount;
stackStep = np.pi/ stackCount;

for i in range(int(stackCount)):
    stackAngle=(np.pi/2)-i*stackStep
    xy=radius*np.cos(stackAngle)
    z=radius*np.sin(stackAngle)

    for j in range(int(sectorCount)):
        sectorAngle = j * sectorStep
        x = xy * np.cos(sectorAngle)            
        y = xy * np.sin(sectorAngle) 

        xx.append(x)
        yy.append(y)
        zz.append(z)

#print("x",xx[1])
fig = plt.figure(figsize = (10,10))
ax = fig.add_subplot(111, projection='3d')

for i in range(len(xx)):
    ##ax.plot_surface(xx[i], yy[i], zz[i], rstride=4, cstride=4, color='b')
    #ax.plot_wireframe(xx[i], yy[i], zz[i],color="r")
    ax.scatter(xx[i], yy[i], zz[i], color="r", s=8.0)
    #ax.quiver(0, 0, 0,xx[i], yy[i], zz[i], color='royalblue',length=1.0, normalize=True, arrow_length_ratio=0.2)
plt.show()

radius,sectorCount,stackCountがパラメータになっています．
デフォでは単位近似球となっています．
pythonの描画ライブラリ，matplotlib.pyplotが必要です．
実行結果はこんな感じ．

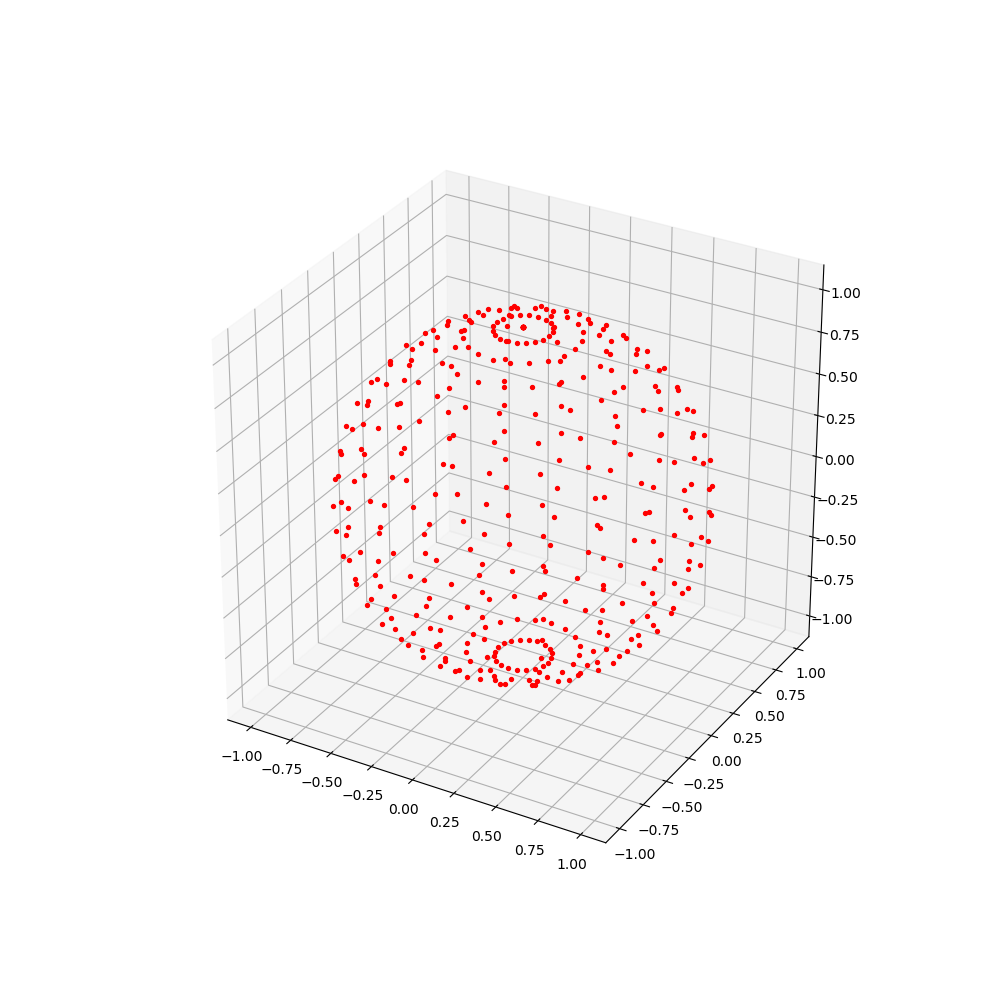
#ax.quiver(0, 0, 0,xx[i], yy[i], zz[i], color='royalblue',length=1.0, normalize=True, arrow_length_ratio=0.2)のコメントを外すと，中心から各頂点に向かう方向ベクトルを可視化することができます．

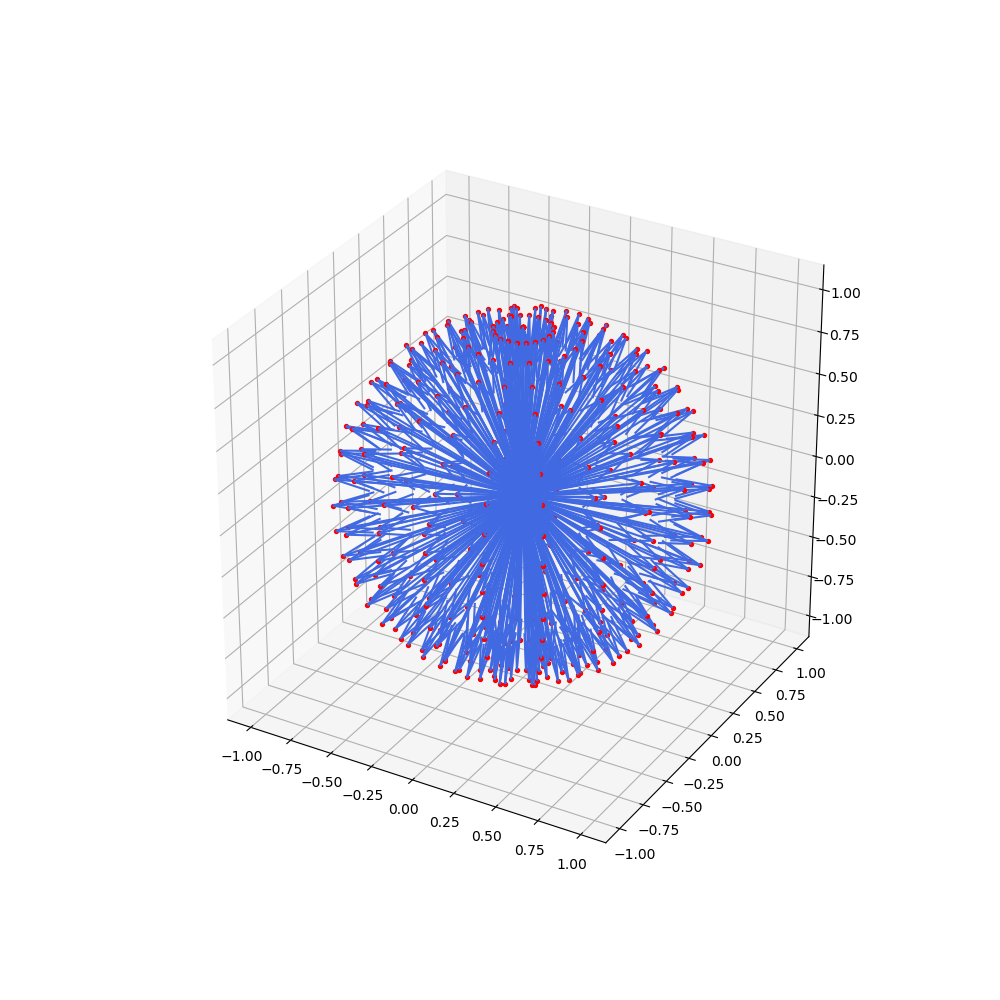
まぁまぁいい感じ？
中心から各頂点までの方向ベクトルを求めることができるので，この方向ベクトルをもとに，物体をランダムに回転させたいなぁと思っています．．．